人教版数学九年级下册第二十七章相似 期中专项复习(word版 含答案)
文档属性
| 名称 | 人教版数学九年级下册第二十七章相似 期中专项复习(word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 312.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-24 12:59:22 | ||
图片预览



文档简介
人教版数学九年级下册第二十七章相似期中专项复习
一、单选题
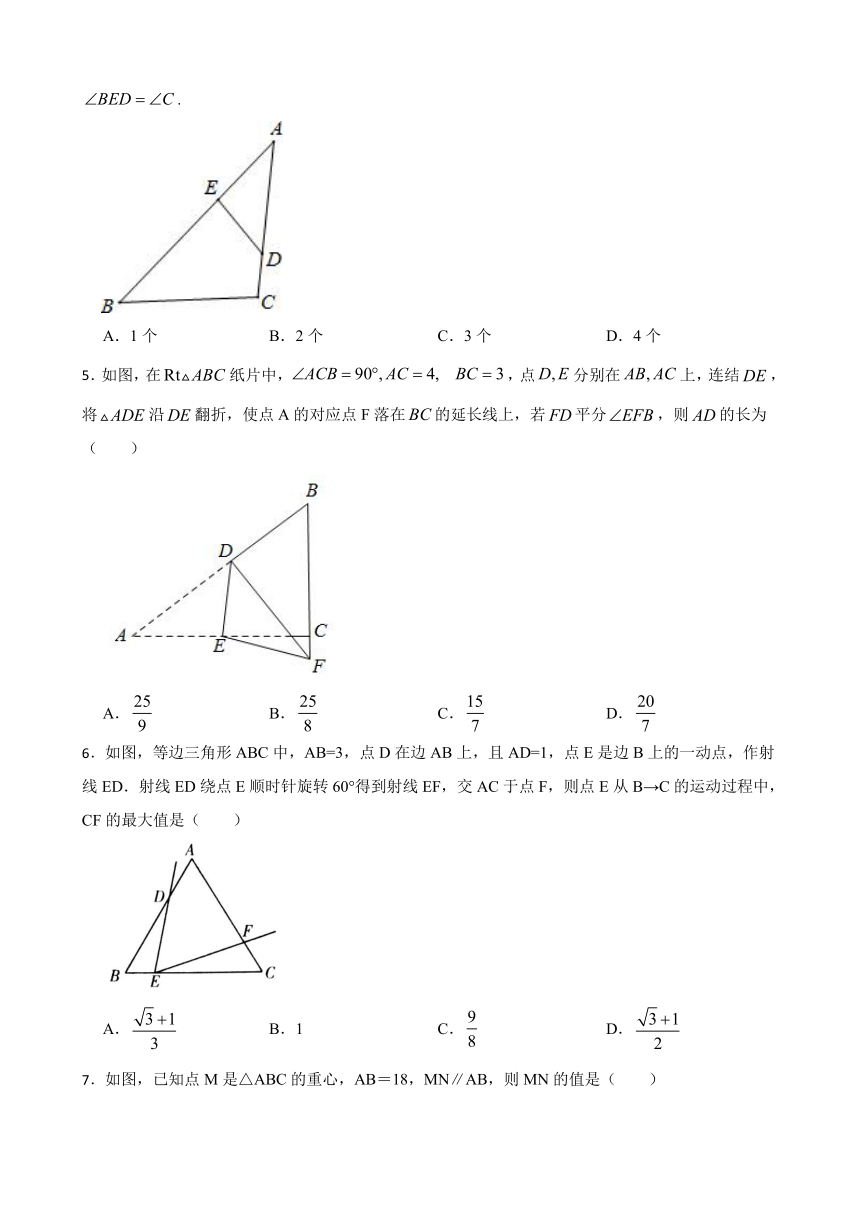
1.如图,取一张长为a,宽为b的长方形纸片,将它对折两次后得到一张小长方形纸片,若要使小长方形与原长方形相似,则原长方形纸片的边a、b应满足的条件是( )
A.a= b B.a=2b C.a=2 b D.a=4b
2.将矩形按照如图所示的方式向外扩张得到新矩形,每条对角线向其延长线两个方向各延伸 ,若所得新矩形与原矩形相似,则a的值的个数可以是( )
A.1 B.2 C.3 D.无数个
3.如图,在平面直角坐标系中,矩形 OABC 的顶点 O 在坐标原点,边 OA 在 x 轴上, OC 在 y 轴上, 如果矩形 与矩形 OABC 关于点 O 位似,且矩形 的面积等于矩形 OABC 面积的 ,那么点 B的坐标是( )
A. B. 或
C. D.(3,2)或(-3,-2)
4.如图,要判定与相似,欲添加一个条件,下列可行的条件有
( 1 );(2);(3);(4);(5).
A.1个 B.2个 C.3个 D.4个
5.如图,在纸片中,,点分别在上,连结,将沿翻折,使点A的对应点F落在的延长线上,若平分,则的长为( )
A. B. C. D.
6.如图,等边三角形ABC中,AB=3,点D在边AB上,且AD=1,点E是边B上的一动点,作射线ED.射线ED绕点E顺时针旋转60°得到射线EF,交AC于点F,则点E从B→C的运动过程中,CF的最大值是( )
A. B.1 C. D.
7.如图,已知点M是△ABC的重心,AB=18,MN∥AB,则MN的值是( )
A.9 B. C. D.6
8.如图,在△ABC与△ADE中,∠ACB=∠AED=90°,∠ABC=∠ADE,连接BD、CE,若AC︰BC=3︰4,则BD︰CE为( )
A.5︰3 B.4︰3 C. ︰2 D.2︰
9.如图,已知△ABC与△DEF位似,位似中心为点O,且AB:DE=3:2,则△ABC的面积与△DEF面积之比为( )
A.3:2 B.3:5 C.9:4 D.9:5
10.如图,正方形ABCD和正方形CGFE的顶点C、D、E在同一直线上,顶点B、C、G在同一条直线上.O是EG的中点,∠EGC的平分线GH过点D,交BE于点H,连接FH交EG于点M,连接OH,以下四个结论:①GH⊥BE;②△EHM∽△FHG;③1;④,其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A出发向B以2cm秒的速度移动;点Q沿DA边从点D开始向A以1cm/秒的速度移动.如果P、Q同时出发,用t秒表示移动的时间(012.在中,,点P在直线上,点P到直线的距离为,则的长为 .
13.已知:,则 .
14.我们知道:四个角对应相等,四条边对应成比例的两个四边形是相似四边形.如图,已知梯形ABCD中,ADBC,AD=1,BC=2,E、F分别是边AB、CD上的点,且EFBC,如果四边AEFD与四边形EBCF相似,那么的值是 .
15.在平面直角坐标系中,已知点E(-4,2),F(-2,-2),以原点O为位似中心,相似比为2,把△EFO放大,则点E的对应点E′的坐标是 .
16.如图,在中,,,,点在边上, ,联结,点在线段上,如果,那么 .
17.如图,在 中,E是 的中点,F在 上,且 , 交 于G.若 ,则 .
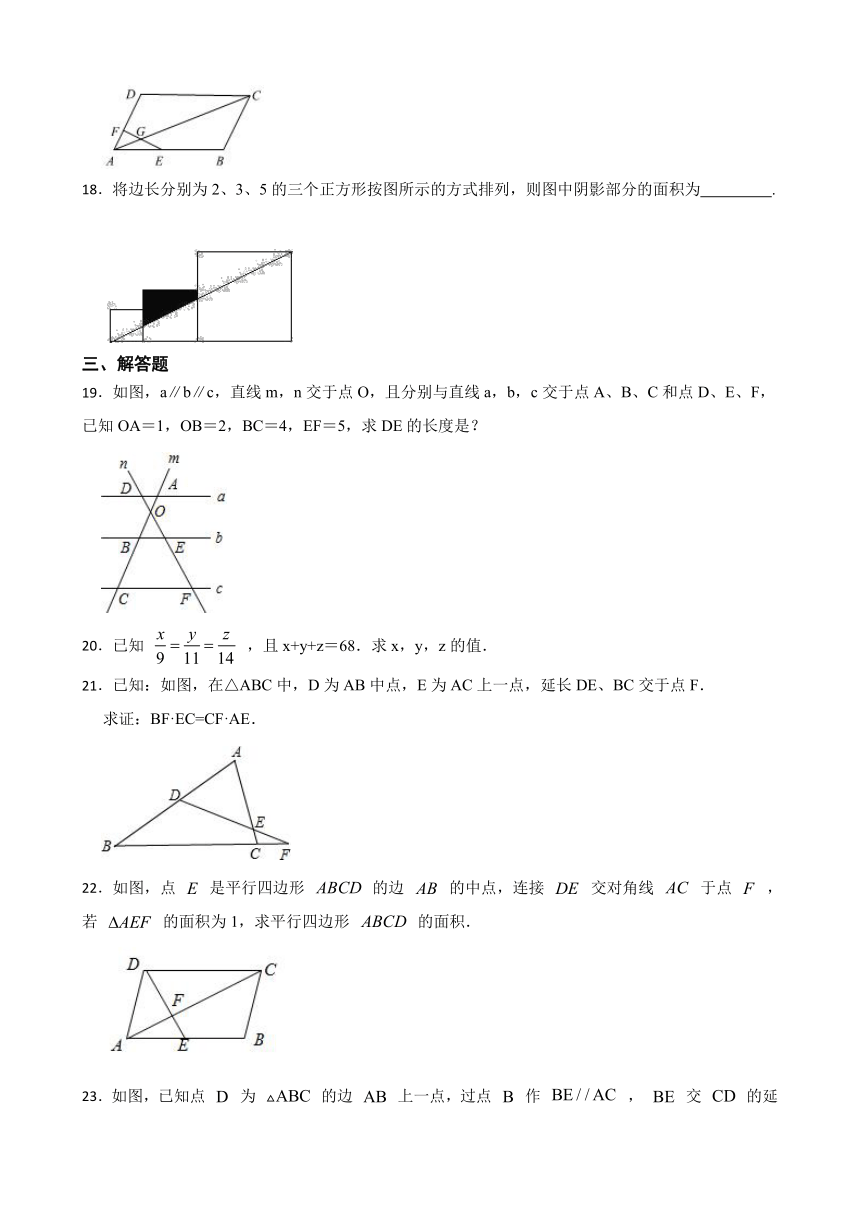
18.将边长分别为2、3、5的三个正方形按图所示的方式排列,则图中阴影部分的面积为 .
三、解答题
19.如图,a∥b∥c,直线m,n交于点O,且分别与直线a,b,c交于点A、B、C和点D、E、F,已知OA=1,OB=2,BC=4,EF=5,求DE的长度是?
20.已知 ,且x+y+z=68.求x,y,z的值.
21.已知:如图,在△ABC中,D为AB中点,E为AC上一点,延长DE、BC交于点F.
求证:BF·EC=CF·AE.
22.如图,点 是平行四边形 的边 的中点,连接 交对角线 于点 ,若 的面积为1,求平行四边形 的面积.
23.如图,已知点 为 的边 上一点,过点 作 , 交 的延长线于点 ,且 , , ,求 的长.
24.已知:如图,在 中, , , 、 分别在 、 上, , .求证: .
25.请阅读下列材料,并完成相应的任务.
正方形网格是认识数和形的绝好途径.在网格中构造几何图形具有直观性和可操作性,网格中的数学问题具有显著的数形结合和转化的特征.下面网格图中每个小正方形的边长都为1.
如图1,点A、B、C、D都是格点,连接AC,BD交于点O,则AC,BD互相平分.
如图2,点A、B、C、D都是格点,连接AC,BD交于点M,则点M是线段AC的四等分点.
任务一:请你观察图1,连接AD、DC、CB、AB,则AC,BD互相平分,其理由是 ▲ .
任务二:请你观察图2,说明点M是AC的四等分点的理由.
任务三:在下面网格图中按要求作图.要求:①仅用无刻度直尺;②保留必要的思考痕迹.
在图3中的线段BC上做两点M、N,使得△ABM与△ABN都为等腰三角形.
答案解析部分
1.【答案】B
2.【答案】D
3.【答案】B
4.【答案】C
5.【答案】D
6.【答案】C
7.【答案】D
8.【答案】A
9.【答案】C
10.【答案】C
11.【答案】1.2s或3s
12.【答案】或
13.【答案】
14.【答案】
15.【答案】(-8,4)或(8,-4)
16.【答案】
17.【答案】8
18.【答案】
19.【答案】解:∵OA=1,OB=2,
∴AB=3,
∵a∥b∥c,
∴ ,
即 ,
∴ ;
∴DE的长度是 .
20.【答案】解:设 ,
则x=9k,y=11k,z=14k,
∴9k+11k+14k=68,
解得:k=2,
∴x=18,y=22,z=28.
答:x,y,z的值分别为18,22,28.
21.【答案】证明:作DG∥BC,DH∥AC,
则△ADG∽△ABC,
∵D是AB中点,
∴G是AC中点,H是BC中点,BC=2DG,AC=2AG,
∵△DGE∽△FCE,
∴ ,
∴ ,即 ,
∴ ,
即 ,
∵EG+EC=GC=AG,
∴EG+EG+EC=EG+AG=AE,
∴ ,即 ,
∴BF·EC=CF·AE.
22.【答案】解:∵四边形 为平行四边形,
∴ ,
∴ ,
∵点 是 的中点,
∴ ,
∴ ,
∵ 的面积为1,
∴ ,
∴ ,
∴平行四边形 的面积= .
23.【答案】解:∵BE∥AC,
∴∠EBD=∠A,∠E=∠ACD,
∵∠ACD=∠ABC,∴∠E=∠ABC,
∴△BED∽△ABC.
∵ ,
∴ ,∴ .
∴ ,解得BD=15.
∵∠ACD=∠ABC,∠A=∠A,
∴△ACD∽△ABC,
∴ ,即 ,
设AD=x,则 ,
解这个方程,得 , (不合题意,舍去),
∴AD=5.
24.【答案】证明:∵ , ,
∴ ,
∵ , ,
∴ ,
∴ , .
∴ ,
∵
∴ .
25.【答案】解:任务一:矩形的对角线互相平分;任务二:如图,连接AD,BC
∵
∴
∴
∴
∴ 是AC的四等分点;
任务三:如图,取点D,E,连接DE,交BC于点M,连接MA,则△MBA是等腰三角形,如图:
理由是:∵
即DE是AB的垂直平分线,
∴MA=MB
∴△MBA是等腰三角形;
取点F,连接AF,AF与BC交于点N,△ABN是等腰三角形,如图:
理由是:AB=4,AC=3,
由勾股定理得,BC=
又CF=1,CF//AB
∴ ,即
∴AB=NB=4
∴△ABN是等腰三角形.
一、单选题
1.如图,取一张长为a,宽为b的长方形纸片,将它对折两次后得到一张小长方形纸片,若要使小长方形与原长方形相似,则原长方形纸片的边a、b应满足的条件是( )
A.a= b B.a=2b C.a=2 b D.a=4b
2.将矩形按照如图所示的方式向外扩张得到新矩形,每条对角线向其延长线两个方向各延伸 ,若所得新矩形与原矩形相似,则a的值的个数可以是( )
A.1 B.2 C.3 D.无数个
3.如图,在平面直角坐标系中,矩形 OABC 的顶点 O 在坐标原点,边 OA 在 x 轴上, OC 在 y 轴上, 如果矩形 与矩形 OABC 关于点 O 位似,且矩形 的面积等于矩形 OABC 面积的 ,那么点 B的坐标是( )
A. B. 或
C. D.(3,2)或(-3,-2)
4.如图,要判定与相似,欲添加一个条件,下列可行的条件有
( 1 );(2);(3);(4);(5).
A.1个 B.2个 C.3个 D.4个
5.如图,在纸片中,,点分别在上,连结,将沿翻折,使点A的对应点F落在的延长线上,若平分,则的长为( )
A. B. C. D.
6.如图,等边三角形ABC中,AB=3,点D在边AB上,且AD=1,点E是边B上的一动点,作射线ED.射线ED绕点E顺时针旋转60°得到射线EF,交AC于点F,则点E从B→C的运动过程中,CF的最大值是( )
A. B.1 C. D.
7.如图,已知点M是△ABC的重心,AB=18,MN∥AB,则MN的值是( )
A.9 B. C. D.6
8.如图,在△ABC与△ADE中,∠ACB=∠AED=90°,∠ABC=∠ADE,连接BD、CE,若AC︰BC=3︰4,则BD︰CE为( )
A.5︰3 B.4︰3 C. ︰2 D.2︰
9.如图,已知△ABC与△DEF位似,位似中心为点O,且AB:DE=3:2,则△ABC的面积与△DEF面积之比为( )
A.3:2 B.3:5 C.9:4 D.9:5
10.如图,正方形ABCD和正方形CGFE的顶点C、D、E在同一直线上,顶点B、C、G在同一条直线上.O是EG的中点,∠EGC的平分线GH过点D,交BE于点H,连接FH交EG于点M,连接OH,以下四个结论:①GH⊥BE;②△EHM∽△FHG;③1;④,其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A出发向B以2cm秒的速度移动;点Q沿DA边从点D开始向A以1cm/秒的速度移动.如果P、Q同时出发,用t秒表示移动的时间(0
13.已知:,则 .
14.我们知道:四个角对应相等,四条边对应成比例的两个四边形是相似四边形.如图,已知梯形ABCD中,ADBC,AD=1,BC=2,E、F分别是边AB、CD上的点,且EFBC,如果四边AEFD与四边形EBCF相似,那么的值是 .
15.在平面直角坐标系中,已知点E(-4,2),F(-2,-2),以原点O为位似中心,相似比为2,把△EFO放大,则点E的对应点E′的坐标是 .
16.如图,在中,,,,点在边上, ,联结,点在线段上,如果,那么 .
17.如图,在 中,E是 的中点,F在 上,且 , 交 于G.若 ,则 .
18.将边长分别为2、3、5的三个正方形按图所示的方式排列,则图中阴影部分的面积为 .
三、解答题
19.如图,a∥b∥c,直线m,n交于点O,且分别与直线a,b,c交于点A、B、C和点D、E、F,已知OA=1,OB=2,BC=4,EF=5,求DE的长度是?
20.已知 ,且x+y+z=68.求x,y,z的值.
21.已知:如图,在△ABC中,D为AB中点,E为AC上一点,延长DE、BC交于点F.
求证:BF·EC=CF·AE.
22.如图,点 是平行四边形 的边 的中点,连接 交对角线 于点 ,若 的面积为1,求平行四边形 的面积.
23.如图,已知点 为 的边 上一点,过点 作 , 交 的延长线于点 ,且 , , ,求 的长.
24.已知:如图,在 中, , , 、 分别在 、 上, , .求证: .
25.请阅读下列材料,并完成相应的任务.
正方形网格是认识数和形的绝好途径.在网格中构造几何图形具有直观性和可操作性,网格中的数学问题具有显著的数形结合和转化的特征.下面网格图中每个小正方形的边长都为1.
如图1,点A、B、C、D都是格点,连接AC,BD交于点O,则AC,BD互相平分.
如图2,点A、B、C、D都是格点,连接AC,BD交于点M,则点M是线段AC的四等分点.
任务一:请你观察图1,连接AD、DC、CB、AB,则AC,BD互相平分,其理由是 ▲ .
任务二:请你观察图2,说明点M是AC的四等分点的理由.
任务三:在下面网格图中按要求作图.要求:①仅用无刻度直尺;②保留必要的思考痕迹.
在图3中的线段BC上做两点M、N,使得△ABM与△ABN都为等腰三角形.
答案解析部分
1.【答案】B
2.【答案】D
3.【答案】B
4.【答案】C
5.【答案】D
6.【答案】C
7.【答案】D
8.【答案】A
9.【答案】C
10.【答案】C
11.【答案】1.2s或3s
12.【答案】或
13.【答案】
14.【答案】
15.【答案】(-8,4)或(8,-4)
16.【答案】
17.【答案】8
18.【答案】
19.【答案】解:∵OA=1,OB=2,
∴AB=3,
∵a∥b∥c,
∴ ,
即 ,
∴ ;
∴DE的长度是 .
20.【答案】解:设 ,
则x=9k,y=11k,z=14k,
∴9k+11k+14k=68,
解得:k=2,
∴x=18,y=22,z=28.
答:x,y,z的值分别为18,22,28.
21.【答案】证明:作DG∥BC,DH∥AC,
则△ADG∽△ABC,
∵D是AB中点,
∴G是AC中点,H是BC中点,BC=2DG,AC=2AG,
∵△DGE∽△FCE,
∴ ,
∴ ,即 ,
∴ ,
即 ,
∵EG+EC=GC=AG,
∴EG+EG+EC=EG+AG=AE,
∴ ,即 ,
∴BF·EC=CF·AE.
22.【答案】解:∵四边形 为平行四边形,
∴ ,
∴ ,
∵点 是 的中点,
∴ ,
∴ ,
∵ 的面积为1,
∴ ,
∴ ,
∴平行四边形 的面积= .
23.【答案】解:∵BE∥AC,
∴∠EBD=∠A,∠E=∠ACD,
∵∠ACD=∠ABC,∴∠E=∠ABC,
∴△BED∽△ABC.
∵ ,
∴ ,∴ .
∴ ,解得BD=15.
∵∠ACD=∠ABC,∠A=∠A,
∴△ACD∽△ABC,
∴ ,即 ,
设AD=x,则 ,
解这个方程,得 , (不合题意,舍去),
∴AD=5.
24.【答案】证明:∵ , ,
∴ ,
∵ , ,
∴ ,
∴ , .
∴ ,
∵
∴ .
25.【答案】解:任务一:矩形的对角线互相平分;任务二:如图,连接AD,BC
∵
∴
∴
∴
∴ 是AC的四等分点;
任务三:如图,取点D,E,连接DE,交BC于点M,连接MA,则△MBA是等腰三角形,如图:
理由是:∵
即DE是AB的垂直平分线,
∴MA=MB
∴△MBA是等腰三角形;
取点F,连接AF,AF与BC交于点N,△ABN是等腰三角形,如图:
理由是:AB=4,AC=3,
由勾股定理得,BC=
又CF=1,CF//AB
∴ ,即
∴AB=NB=4
∴△ABN是等腰三角形.
