人教版数学第二十六章《反比例函数》基础复习题(word,含答案)
文档属性
| 名称 | 人教版数学第二十六章《反比例函数》基础复习题(word,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 186.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-24 10:55:15 | ||
图片预览


文档简介
人教版数学第二十六章反比例函数基础复习
一、单选题
1.在下列函数中表示y关于x 的反比例函数的是( )
A.y=2x B. C. D.
2.已知函数y=(m+2)x 是反比例函数,则m的值是( )
A.2 B. C. D.
3.下列选项,是反比例函数关系的为( )
A.在直角三角形中,30°角所对的直角边 与斜边 之间的关系
B.在等腰三角形中,顶角 与底角 之间的关系
C.圆的面积 与它的直径 之间的关系
D.面积为20的菱形,其中一条对角线 与另一条对角线 之间的关系
4.某物体对地面的压力为定值,物体对地面的压强 与受力面积 之间的函数关系如图所示,这一函数表达式为( )
A. B. C. D.
5.已知点M(-2,4)在双曲线y= 上,则下列各点一定在该双曲线上的是( )
A.(-2,-4) B.(4,-2) C.(2,4) D.(4,2)
6.已知反比例函数的解析式为 ,则a的取值范围是
A. B. C. D.
7.矩形的面积为4,它的长 与宽 之间的函数关系用图象大致可表示为( )
A. B.
C. D.
8.若点,,都在反比例函的图象上,则,,的大小关系是( )
A. B. C. D.
9.在同一直角坐标系中,函数 与 的图象大致为( ).
A. B.
C. D.
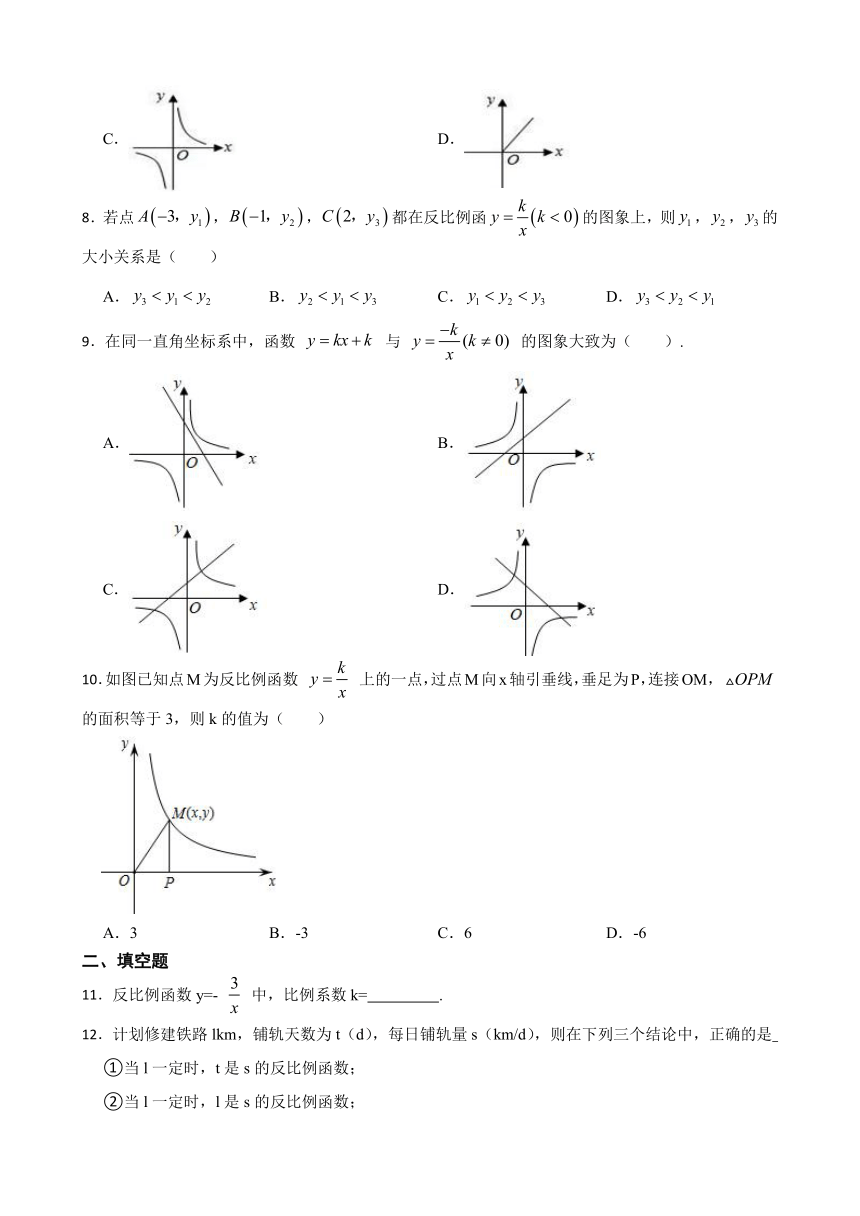
10.如图已知点M为反比例函数 上的一点,过点M向x轴引垂线,垂足为P,连接OM, 的面积等于3,则k的值为( )
A.3 B.-3 C.6 D.-6
二、填空题
11.反比例函数y=- 中,比例系数k= .
12.计划修建铁路lkm,铺轨天数为t(d),每日铺轨量s(km/d),则在下列三个结论中,正确的是
①当l一定时,t是s的反比例函数;
②当l一定时,l是s的反比例函数;
③当s一定时,l是t的反比例函数.
13.函数y= 是 反比例函数,则m的值是 .
14.若 与 成反比例关系, 与 成反比例关系,则 与 成 关系.
15.如图,已知双曲线y= (k>0)经过Rt△OAB的直角边AB的中点C,与斜边OB相交于点D,若OD=1,则BD= .
16.如图,点A是反比例函数图象上的一点,过点A作AC⊥x轴,垂足为点C,D为AC的中点,若△AOD的面积为1,则k的值为 .
17.若反比例函数y 的图象落在第一、三象限内,则m满足的条件是 .
18.小刚欲用撬棍撬动一块大石头,已知阻力和阻力臂不变,分别为900牛顿和0.5米,则当动力臂为1.5米时,撬动石头需要的力大于 牛顿.(提示根据杠杆原理:阻力x阻力臂=动力x动力臂)
三、解答题
19.已知y是x的反比例函数,且当x=2时,y=﹣3,请你确定该反比例函数的解析式,并求当y=6时,自变量x的值.
20.已知函数y=(m2+2m)
(1)如果y是x的正比例函数,求m的值;
(2)如果y是x的反比例函数,求出m的值,并写出此时y与x的函数关系式.
21.已知点A(m,p),B(n,q)(m<n<0)在动点C(,a)(k≠0)所形成的曲线上.若p+q=﹣b﹣2,﹣1.试比较p和q的大小,并说明理由.
22.已知一个面积为60的平行四边形,设它的其中一边长为x,这边上的高为y,试写出y与x的函数关系式,并判断它是什么函数.
23.已知经过闭合电路的电流I与电路的电阻R是反比例函数关系,请根据表格已知条件求出I与R的反比例函数关系式,并填写表格中的空格.
I(安) 5 10
R(欧)
10
24.如图所示,Rt△AOB中,∠AOB=90°,OA=10,点B在反比例函数y=图象上,且点B的横坐标为3.
(1)求OB的长;
(2)求过点A的双曲线的解析式.
25.如图,反比例函数y=在第一象限的图象经过矩形OABC对角线的交点E,与BC交于点D,若点B的坐标为(6,4).
(1)求E点的坐标及k的值;
(2)求△OCD的面积.
答案解析部分
1.【答案】B
2.【答案】A
3.【答案】D
4.【答案】B
5.【答案】B
6.【答案】C
7.【答案】B
8.【答案】A
9.【答案】B
10.【答案】C
11.【答案】-3
12.【答案】①
13.【答案】5
14.【答案】正比例
15.【答案】 ﹣1
16.【答案】4
17.【答案】
18.【答案】300
19.【答案】解:设反比例函数y= (k≠0),
∵当x=2时,y=﹣3,
∴k=xy=2×(﹣3)=﹣6,
∴y与x之间的函数关系式y=﹣ .
把y=6代入y=﹣ ,则x=﹣1
20.【答案】解:(1)由y=(m2+2m)是正比例函数,得
m2﹣m﹣1=1且m2+2m≠0,
解得m=2或m=﹣1;
(2)由y=(m2+2m)是反比例函数,得
m2﹣m﹣1=﹣1且m2+2m≠0,
解得m=1.
故y与x的函数关系式y=3x﹣1.
21.【答案】解:∵A(m,p),B(n,q)(m<n<0)在动点C(,a)(k≠0)所形成的曲线上.
∴p=,q=.
∴p+q=.
∵p+q=﹣b﹣2,
∴﹣b﹣2=k (﹣1),
∴k=b2+2b+2=(b+1)2+1>0,
∵m<n<0,p=,q=.
∴p>q.
22.【答案】解:∵xy=60,
∴y=,
∴y是x的反比例函数.
23.【答案】解:依题意设,
把I=10,R=10代入得:,
解得U=100,
所以.
100÷5=20.
I(安) 5 10
R(欧) 20 10
24.【答案】解:(1)过点B作BD⊥x轴于D,∵点B在反比例函数y=图象上,且点B的横坐标为3,∴y=4,∴BD=4,OD=3,∴OB==5;(2)过点A作AC⊥x轴于C,∴∠ACO=∠BDO=90°,∵∠AOB=90°,∴∠AOC+∠CAO=∠AOC+∠BOD=90°,∴∠CAO=∠BOD,∴△ACO∽△ODB,∴=2,∴AC=6,OC=8,∴A(﹣6,8),设过A 的反比例函数的解析式为:y=,∴k=﹣48,∴过点A的双曲线的解析式y=﹣.
25.【答案】解:(1)∵E是矩形OABC对角线的交点,
∴OE=EB,
∵点B的坐标为(6,4),
∴E点的坐标是(3,2),
把x=3,y=2代入y=得k=6;
(2)设点D的坐标为(x,y),则S△OCD=OC×OD,
即S△OCD=xy=k,
由(1)知k=6,
∴S△OCD=k=3.
一、单选题
1.在下列函数中表示y关于x 的反比例函数的是( )
A.y=2x B. C. D.
2.已知函数y=(m+2)x 是反比例函数,则m的值是( )
A.2 B. C. D.
3.下列选项,是反比例函数关系的为( )
A.在直角三角形中,30°角所对的直角边 与斜边 之间的关系
B.在等腰三角形中,顶角 与底角 之间的关系
C.圆的面积 与它的直径 之间的关系
D.面积为20的菱形,其中一条对角线 与另一条对角线 之间的关系
4.某物体对地面的压力为定值,物体对地面的压强 与受力面积 之间的函数关系如图所示,这一函数表达式为( )
A. B. C. D.
5.已知点M(-2,4)在双曲线y= 上,则下列各点一定在该双曲线上的是( )
A.(-2,-4) B.(4,-2) C.(2,4) D.(4,2)
6.已知反比例函数的解析式为 ,则a的取值范围是
A. B. C. D.
7.矩形的面积为4,它的长 与宽 之间的函数关系用图象大致可表示为( )
A. B.
C. D.
8.若点,,都在反比例函的图象上,则,,的大小关系是( )
A. B. C. D.
9.在同一直角坐标系中,函数 与 的图象大致为( ).
A. B.
C. D.
10.如图已知点M为反比例函数 上的一点,过点M向x轴引垂线,垂足为P,连接OM, 的面积等于3,则k的值为( )
A.3 B.-3 C.6 D.-6
二、填空题
11.反比例函数y=- 中,比例系数k= .
12.计划修建铁路lkm,铺轨天数为t(d),每日铺轨量s(km/d),则在下列三个结论中,正确的是
①当l一定时,t是s的反比例函数;
②当l一定时,l是s的反比例函数;
③当s一定时,l是t的反比例函数.
13.函数y= 是 反比例函数,则m的值是 .
14.若 与 成反比例关系, 与 成反比例关系,则 与 成 关系.
15.如图,已知双曲线y= (k>0)经过Rt△OAB的直角边AB的中点C,与斜边OB相交于点D,若OD=1,则BD= .
16.如图,点A是反比例函数图象上的一点,过点A作AC⊥x轴,垂足为点C,D为AC的中点,若△AOD的面积为1,则k的值为 .
17.若反比例函数y 的图象落在第一、三象限内,则m满足的条件是 .
18.小刚欲用撬棍撬动一块大石头,已知阻力和阻力臂不变,分别为900牛顿和0.5米,则当动力臂为1.5米时,撬动石头需要的力大于 牛顿.(提示根据杠杆原理:阻力x阻力臂=动力x动力臂)
三、解答题
19.已知y是x的反比例函数,且当x=2时,y=﹣3,请你确定该反比例函数的解析式,并求当y=6时,自变量x的值.
20.已知函数y=(m2+2m)
(1)如果y是x的正比例函数,求m的值;
(2)如果y是x的反比例函数,求出m的值,并写出此时y与x的函数关系式.
21.已知点A(m,p),B(n,q)(m<n<0)在动点C(,a)(k≠0)所形成的曲线上.若p+q=﹣b﹣2,﹣1.试比较p和q的大小,并说明理由.
22.已知一个面积为60的平行四边形,设它的其中一边长为x,这边上的高为y,试写出y与x的函数关系式,并判断它是什么函数.
23.已知经过闭合电路的电流I与电路的电阻R是反比例函数关系,请根据表格已知条件求出I与R的反比例函数关系式,并填写表格中的空格.
I(安) 5 10
R(欧)
10
24.如图所示,Rt△AOB中,∠AOB=90°,OA=10,点B在反比例函数y=图象上,且点B的横坐标为3.
(1)求OB的长;
(2)求过点A的双曲线的解析式.
25.如图,反比例函数y=在第一象限的图象经过矩形OABC对角线的交点E,与BC交于点D,若点B的坐标为(6,4).
(1)求E点的坐标及k的值;
(2)求△OCD的面积.
答案解析部分
1.【答案】B
2.【答案】A
3.【答案】D
4.【答案】B
5.【答案】B
6.【答案】C
7.【答案】B
8.【答案】A
9.【答案】B
10.【答案】C
11.【答案】-3
12.【答案】①
13.【答案】5
14.【答案】正比例
15.【答案】 ﹣1
16.【答案】4
17.【答案】
18.【答案】300
19.【答案】解:设反比例函数y= (k≠0),
∵当x=2时,y=﹣3,
∴k=xy=2×(﹣3)=﹣6,
∴y与x之间的函数关系式y=﹣ .
把y=6代入y=﹣ ,则x=﹣1
20.【答案】解:(1)由y=(m2+2m)是正比例函数,得
m2﹣m﹣1=1且m2+2m≠0,
解得m=2或m=﹣1;
(2)由y=(m2+2m)是反比例函数,得
m2﹣m﹣1=﹣1且m2+2m≠0,
解得m=1.
故y与x的函数关系式y=3x﹣1.
21.【答案】解:∵A(m,p),B(n,q)(m<n<0)在动点C(,a)(k≠0)所形成的曲线上.
∴p=,q=.
∴p+q=.
∵p+q=﹣b﹣2,
∴﹣b﹣2=k (﹣1),
∴k=b2+2b+2=(b+1)2+1>0,
∵m<n<0,p=,q=.
∴p>q.
22.【答案】解:∵xy=60,
∴y=,
∴y是x的反比例函数.
23.【答案】解:依题意设,
把I=10,R=10代入得:,
解得U=100,
所以.
100÷5=20.
I(安) 5 10
R(欧) 20 10
24.【答案】解:(1)过点B作BD⊥x轴于D,∵点B在反比例函数y=图象上,且点B的横坐标为3,∴y=4,∴BD=4,OD=3,∴OB==5;(2)过点A作AC⊥x轴于C,∴∠ACO=∠BDO=90°,∵∠AOB=90°,∴∠AOC+∠CAO=∠AOC+∠BOD=90°,∴∠CAO=∠BOD,∴△ACO∽△ODB,∴=2,∴AC=6,OC=8,∴A(﹣6,8),设过A 的反比例函数的解析式为:y=,∴k=﹣48,∴过点A的双曲线的解析式y=﹣.
25.【答案】解:(1)∵E是矩形OABC对角线的交点,
∴OE=EB,
∵点B的坐标为(6,4),
∴E点的坐标是(3,2),
把x=3,y=2代入y=得k=6;
(2)设点D的坐标为(x,y),则S△OCD=OC×OD,
即S△OCD=xy=k,
由(1)知k=6,
∴S△OCD=k=3.
