7.5 正态分布(1)(共17张PPT)
文档属性
| 名称 | 7.5 正态分布(1)(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-24 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
正态分布(1)
正态分布(1)
导语
问题1 下列随机变量是否是离散型随机变量:
(1)掷一枚骰子一次,用X表示所得点数;
是
(2)自动流水线包装的食盐,每袋标准质量为400g.由于各种不可控的因素,
任意抽取一袋食盐,用X表示它与标准质量之间的误差(实际质量减去标准质量).
不是
可能取值为有限个或可以一一列举的随机变量
取值往往充满某个区间甚至整个实轴,但取一点的概率为0
连续型随机变量
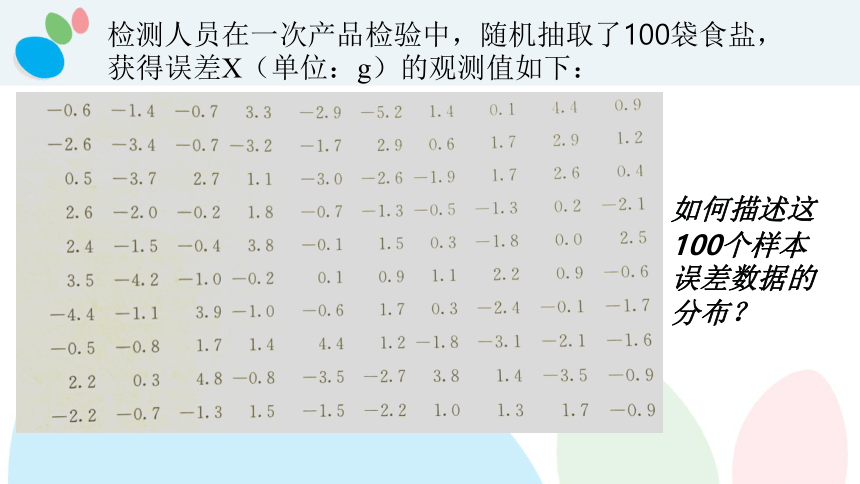
检测人员在一次产品检验中,随机抽取了100袋食盐,
获得误差X(单位:g)的观测值如下:
如何描述这100个样本误差数据的分布?
如何描述这100个样本误差数据的分布?
随着样本数据量越来越大,让分组越来越多,组距越来越小,由频率的稳定性可知,频率分布直方图的轮廓越来越稳定,接近一条光滑的钟形曲线.
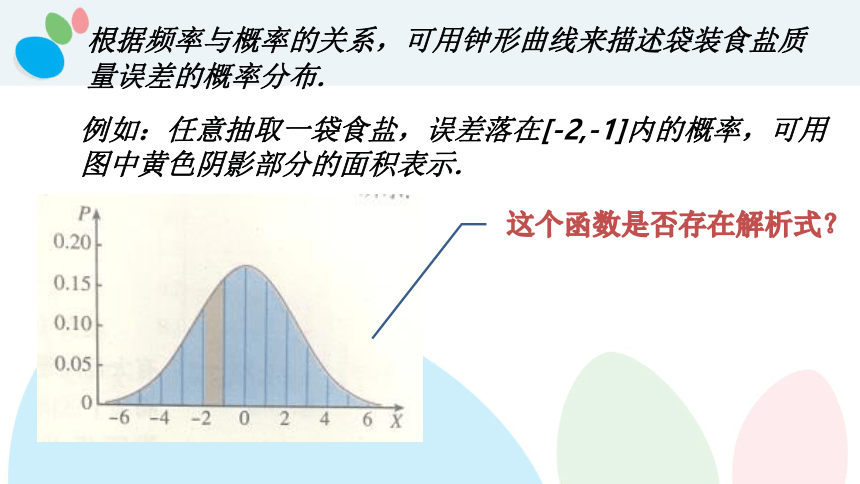
根据频率与概率的关系,可用钟形曲线来描述袋装食盐质量误差的概率分布.
例如:任意抽取一袋食盐,误差落在[-2,-1]内的概率,可用图中黄色阴影部分的面积表示.
这个函数是否存在解析式?
知识梳理
1.我们称f(x)=________________,x∈R,其中μ∈R,σ>0为参数,为 ,称它的图象为正态密度曲线,简称 .
正态密度函数
正态曲线
2.若随机变量X的概率分布密度函数为f(x),则称随机变量X服从正态分布,记为 .特别地,当μ=0,σ=1时,称随机变量X服从 .
X~N(μ,σ2)
标准正态分布
思考:正态曲线f(x)= ,x∈R中的参数μ,
σ有何意义?
答案: μ可取任意实数,表示平均水平的特征数,E(X)=μ;
σ>0表示标准差,D(X)=σ2.
一个正态密度函数由μ,σ唯一确定,π和e为常数,
x为自变量,x∈R.
例1 已知随机变量服从正态分布,其正态曲线如图所示,则总体的均值μ=______,方差σ2=_____.
f(x)=
反思感悟 利用正态曲线的特点求参数μ,σ
(1)正态曲线是单峰的,它关于直线x=μ对称,
由此特点结合图象求出μ.
20
2
正态曲线的特点
1.对 x∈R,f(x)>0,它的图象在x轴的 .
2.曲线与x轴之间的面积为 .
3.曲线是单峰的,它关于直线 对称.
4.曲线在 处达到峰值 .
5.当|x|无限增大时,曲线无限接近 轴.
上方
1
x=μ
x=μ
x
6.当 一定时,曲线的位置由μ确定,曲线随着 的变化而沿x轴平移,如图①.
σ
μ
f(x)=
7.当μ一定时,曲线的形状由σ确定,σ较小时曲线“瘦高”,表示随机变量X的分布比较集中;σ较大时,曲线“矮胖”,表示随机变量X的分布比较分散,如图②.
例2 (多选)下面给出的关于正态曲线的4个叙述中,正确的有
A.曲线在x轴上方,且与x轴不相交
B.当x>μ时,曲线下降,当x<μ时,曲线上升
C.当μ一定时,σ越小,总体分布越分散,σ越大,总体分布越集中
D.曲线关于直线x=μ对称,且当x=μ时,位于最高点
变式:如图所示是当σ取三个不同值σ1,σ2,σ3的三种正态曲线N(0,σ2)的图象,那么σ1,σ2,σ3的大小关系是
A.σ1>1>σ2>σ3>0
B.0<σ1<σ2<1<σ3
C.σ1>σ2>1>σ3>0
D.0<σ1<σ2=1<σ3
若X~N(μ,σ2),如图所示,
X取值不超过x的概率P(X≤x)为图中区域A的面积,
而P(a≤X≤b)为区域B的面积.
X可取(a,b]内的任何值,
故X不是离散型随机变量,
它是连续型随机变量.
例3
(1)已知随机变量X~N(2,σ2),如图所示,
若P(X解析 ∵随机变量X~N(2,σ2),
∴μ=2,由正态分布图象的对称性,可得曲线关于直线x=2对称,
∴P(X>4-a)=P(X∴P(a≤X≤4-a)=1-P(X4-a)=1-2P(X例3
(2)若随机变量ξ~N(10,σ2),P(9≤ξ≤11)=0.4,则P(ξ>11)=_____.
解析 由P(9≤ξ≤11)=0.4且正态曲线以x=μ=10为对称轴知,
P(9≤ξ≤11)=2P(10≤ξ≤11)=0.4.
P(10≤ξ≤11)=0.2,
∵P(ξ≥10)=0.5,
∴P(ξ>11)=0.5-0.2=0.3.
课堂小结
1.知识清单:
(1)正态曲线及其特点.
(2)正态分布的简单应用.
2.方法归纳:转化化归、数形结合.
正态分布(1)
正态分布(1)
导语
问题1 下列随机变量是否是离散型随机变量:
(1)掷一枚骰子一次,用X表示所得点数;
是
(2)自动流水线包装的食盐,每袋标准质量为400g.由于各种不可控的因素,
任意抽取一袋食盐,用X表示它与标准质量之间的误差(实际质量减去标准质量).
不是
可能取值为有限个或可以一一列举的随机变量
取值往往充满某个区间甚至整个实轴,但取一点的概率为0
连续型随机变量
检测人员在一次产品检验中,随机抽取了100袋食盐,
获得误差X(单位:g)的观测值如下:
如何描述这100个样本误差数据的分布?
如何描述这100个样本误差数据的分布?
随着样本数据量越来越大,让分组越来越多,组距越来越小,由频率的稳定性可知,频率分布直方图的轮廓越来越稳定,接近一条光滑的钟形曲线.
根据频率与概率的关系,可用钟形曲线来描述袋装食盐质量误差的概率分布.
例如:任意抽取一袋食盐,误差落在[-2,-1]内的概率,可用图中黄色阴影部分的面积表示.
这个函数是否存在解析式?
知识梳理
1.我们称f(x)=________________,x∈R,其中μ∈R,σ>0为参数,为 ,称它的图象为正态密度曲线,简称 .
正态密度函数
正态曲线
2.若随机变量X的概率分布密度函数为f(x),则称随机变量X服从正态分布,记为 .特别地,当μ=0,σ=1时,称随机变量X服从 .
X~N(μ,σ2)
标准正态分布
思考:正态曲线f(x)= ,x∈R中的参数μ,
σ有何意义?
答案: μ可取任意实数,表示平均水平的特征数,E(X)=μ;
σ>0表示标准差,D(X)=σ2.
一个正态密度函数由μ,σ唯一确定,π和e为常数,
x为自变量,x∈R.
例1 已知随机变量服从正态分布,其正态曲线如图所示,则总体的均值μ=______,方差σ2=_____.
f(x)=
反思感悟 利用正态曲线的特点求参数μ,σ
(1)正态曲线是单峰的,它关于直线x=μ对称,
由此特点结合图象求出μ.
20
2
正态曲线的特点
1.对 x∈R,f(x)>0,它的图象在x轴的 .
2.曲线与x轴之间的面积为 .
3.曲线是单峰的,它关于直线 对称.
4.曲线在 处达到峰值 .
5.当|x|无限增大时,曲线无限接近 轴.
上方
1
x=μ
x=μ
x
6.当 一定时,曲线的位置由μ确定,曲线随着 的变化而沿x轴平移,如图①.
σ
μ
f(x)=
7.当μ一定时,曲线的形状由σ确定,σ较小时曲线“瘦高”,表示随机变量X的分布比较集中;σ较大时,曲线“矮胖”,表示随机变量X的分布比较分散,如图②.
例2 (多选)下面给出的关于正态曲线的4个叙述中,正确的有
A.曲线在x轴上方,且与x轴不相交
B.当x>μ时,曲线下降,当x<μ时,曲线上升
C.当μ一定时,σ越小,总体分布越分散,σ越大,总体分布越集中
D.曲线关于直线x=μ对称,且当x=μ时,位于最高点
变式:如图所示是当σ取三个不同值σ1,σ2,σ3的三种正态曲线N(0,σ2)的图象,那么σ1,σ2,σ3的大小关系是
A.σ1>1>σ2>σ3>0
B.0<σ1<σ2<1<σ3
C.σ1>σ2>1>σ3>0
D.0<σ1<σ2=1<σ3
若X~N(μ,σ2),如图所示,
X取值不超过x的概率P(X≤x)为图中区域A的面积,
而P(a≤X≤b)为区域B的面积.
X可取(a,b]内的任何值,
故X不是离散型随机变量,
它是连续型随机变量.
例3
(1)已知随机变量X~N(2,σ2),如图所示,
若P(X
∴μ=2,由正态分布图象的对称性,可得曲线关于直线x=2对称,
∴P(X>4-a)=P(X
(2)若随机变量ξ~N(10,σ2),P(9≤ξ≤11)=0.4,则P(ξ>11)=_____.
解析 由P(9≤ξ≤11)=0.4且正态曲线以x=μ=10为对称轴知,
P(9≤ξ≤11)=2P(10≤ξ≤11)=0.4.
P(10≤ξ≤11)=0.2,
∵P(ξ≥10)=0.5,
∴P(ξ>11)=0.5-0.2=0.3.
课堂小结
1.知识清单:
(1)正态曲线及其特点.
(2)正态分布的简单应用.
2.方法归纳:转化化归、数形结合.
