5.1.2 弧度制 课件(20张PPT)
文档属性
| 名称 | 5.1.2 弧度制 课件(20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-23 18:04:34 | ||
图片预览





文档简介
(共20张PPT)
“周而复始”
数学模型
P
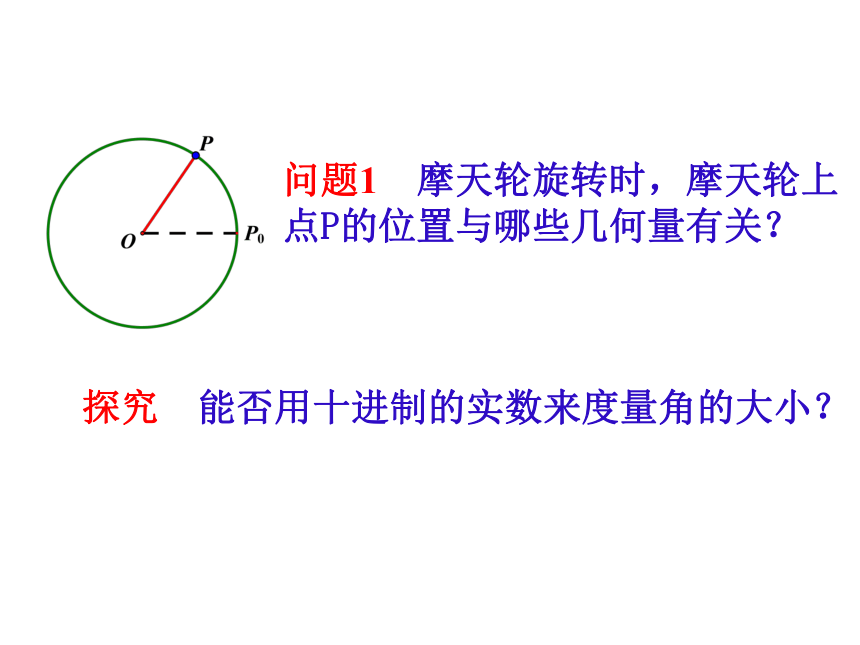
问题1 摩天轮旋转时,摩天轮上点P的位置与哪些几何量有关?
探究 能否用十进制的实数来度量角的大小?
弧度制
问题2 现实生活中,有没有同一个量,它的度量结果可以用不同的单位表示?请举例说一说.
问题3 角度制中,1度角的大小是怎样规定的?
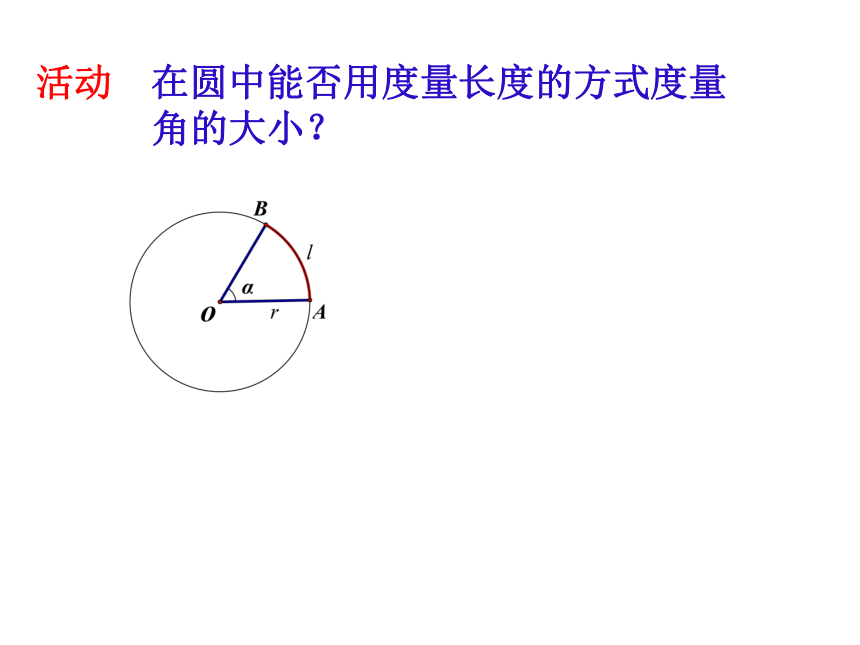
活动 在圆中能否用度量长度的方式度量
角的大小?
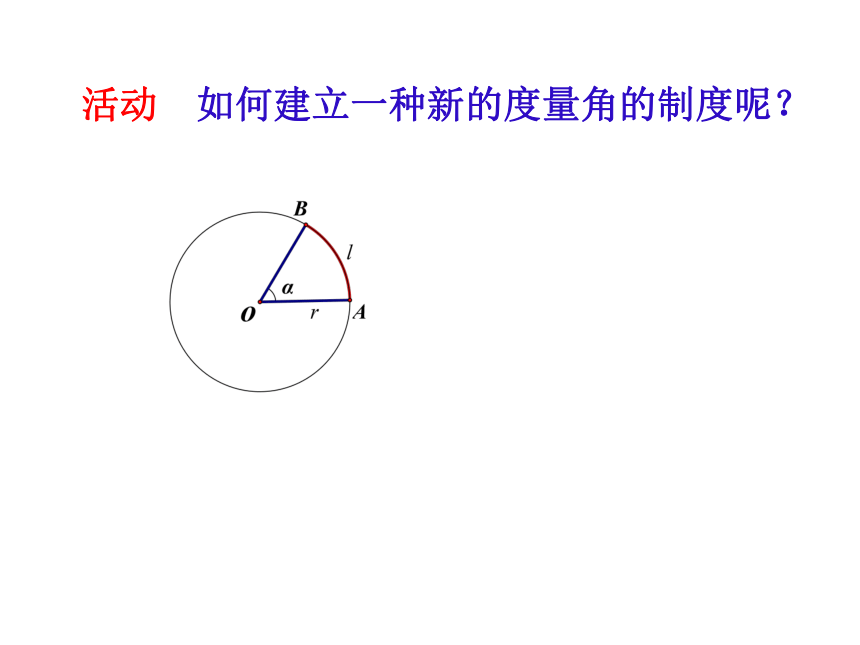
活动 如何建立一种新的度量角的制度呢?
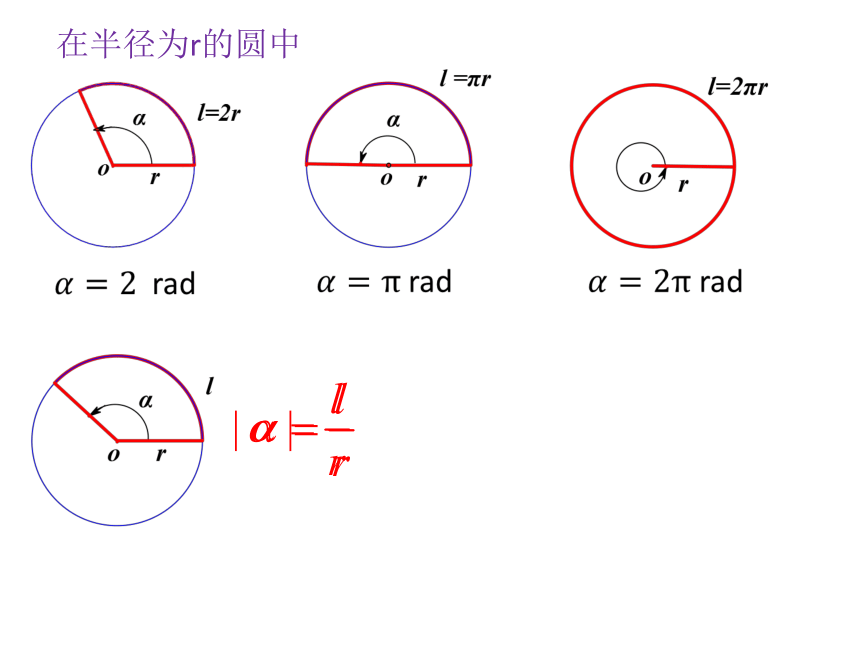
把长度等于半径长的弧所对的圆心角叫做1弧度(radian)的角,记作1rad. 用弧度作为角的单位来度量角的单位制称为弧度制.
数学教师汤姆生(James Thomson)在一次数学考试题目中创造性地首先使用了“弧度一词”,当时他将“半径”(radius)的前四个字母与“角(angle)的前两个字母合在一起,构成radian,并被人们广泛接受和引用.
在半径为r的圆中
问题4 弧度与角度如何换算?
0°
90°
180°
互化练习:
请将量角器上各角进行弧度与角度的互化.
0
π
30°
45°
60°
120°
135°
150°
角度制 弧度制
单位
进制
定义
平角
周角
度
弧度
60进制
10进制
长度等于半径长的弧所对的圆心角
无论是弧度还是度为单位,角的大小都是一个与半径大小无关的值
问题5 说说弧度制与角度制的联系与区别?
例1 把下列各角从弧度化为度
例2 把下列各角从度化为弧度
用弧度来度量角,实际上角的集合
与实数集R之间建立一一对应的关系:
实数集R
正角
零角
负角
正实数
零
负实数
对应角的弧度数
角的集合
问题6 弧度制下,扇形的弧长与面积公式分别
是什么?
弧度制的优越性!
弧长公式
弧度制下
角度制下
l是扇形弧长,r是圆的半径,扇形圆心角的大小为α rad,其中(|α|≤2π)
扇形面积公式
例3 已知扇形的周长为8cm,圆心角为 2rad,求该扇形的面积.
课堂小结
(3)你认为利用弧度制我们可以解决怎样的问题?
(1)本节课我们研究了度量角的另一种制度—弧度制,回顾一下研究过程,我们是怎样来展开对弧度制研究?
(2)你认为定义单位度量角时,应该注意哪些问题?
为何引入弧度制
怎样引入弧度制
弧度制的本质
弧度制与角度制
的联系与区别
弧度制价值与用途
课堂小结
度量需要
制定单位
定量表示
单位换算
度量过程
单位是将整体转化为部分,使之可测量,可比较的工具。
由此,弧度制的引入又给我们用数学的眼光看世界提供了一个工具,更为我们提供了表达世界的另一种方式。
课后作业:
1、(必做)课本P9:练习1-8
P10:习题10、11
2、(选做)查阅弧度制的历史及有关欧拉的资料,进一步明确弧度制的优点,了解欧拉在数学史上的贡献.
谢谢
“周而复始”
数学模型
P
问题1 摩天轮旋转时,摩天轮上点P的位置与哪些几何量有关?
探究 能否用十进制的实数来度量角的大小?
弧度制
问题2 现实生活中,有没有同一个量,它的度量结果可以用不同的单位表示?请举例说一说.
问题3 角度制中,1度角的大小是怎样规定的?
活动 在圆中能否用度量长度的方式度量
角的大小?
活动 如何建立一种新的度量角的制度呢?
把长度等于半径长的弧所对的圆心角叫做1弧度(radian)的角,记作1rad. 用弧度作为角的单位来度量角的单位制称为弧度制.
数学教师汤姆生(James Thomson)在一次数学考试题目中创造性地首先使用了“弧度一词”,当时他将“半径”(radius)的前四个字母与“角(angle)的前两个字母合在一起,构成radian,并被人们广泛接受和引用.
在半径为r的圆中
问题4 弧度与角度如何换算?
0°
90°
180°
互化练习:
请将量角器上各角进行弧度与角度的互化.
0
π
30°
45°
60°
120°
135°
150°
角度制 弧度制
单位
进制
定义
平角
周角
度
弧度
60进制
10进制
长度等于半径长的弧所对的圆心角
无论是弧度还是度为单位,角的大小都是一个与半径大小无关的值
问题5 说说弧度制与角度制的联系与区别?
例1 把下列各角从弧度化为度
例2 把下列各角从度化为弧度
用弧度来度量角,实际上角的集合
与实数集R之间建立一一对应的关系:
实数集R
正角
零角
负角
正实数
零
负实数
对应角的弧度数
角的集合
问题6 弧度制下,扇形的弧长与面积公式分别
是什么?
弧度制的优越性!
弧长公式
弧度制下
角度制下
l是扇形弧长,r是圆的半径,扇形圆心角的大小为α rad,其中(|α|≤2π)
扇形面积公式
例3 已知扇形的周长为8cm,圆心角为 2rad,求该扇形的面积.
课堂小结
(3)你认为利用弧度制我们可以解决怎样的问题?
(1)本节课我们研究了度量角的另一种制度—弧度制,回顾一下研究过程,我们是怎样来展开对弧度制研究?
(2)你认为定义单位度量角时,应该注意哪些问题?
为何引入弧度制
怎样引入弧度制
弧度制的本质
弧度制与角度制
的联系与区别
弧度制价值与用途
课堂小结
度量需要
制定单位
定量表示
单位换算
度量过程
单位是将整体转化为部分,使之可测量,可比较的工具。
由此,弧度制的引入又给我们用数学的眼光看世界提供了一个工具,更为我们提供了表达世界的另一种方式。
课后作业:
1、(必做)课本P9:练习1-8
P10:习题10、11
2、(选做)查阅弧度制的历史及有关欧拉的资料,进一步明确弧度制的优点,了解欧拉在数学史上的贡献.
谢谢
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
