3.1.3 函数的奇偶性 课件(共18张PPT)
文档属性
| 名称 | 3.1.3 函数的奇偶性 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-24 17:16:44 | ||
图片预览




文档简介
(共18张PPT)
人教B版教材必修第一册
函数的奇偶性
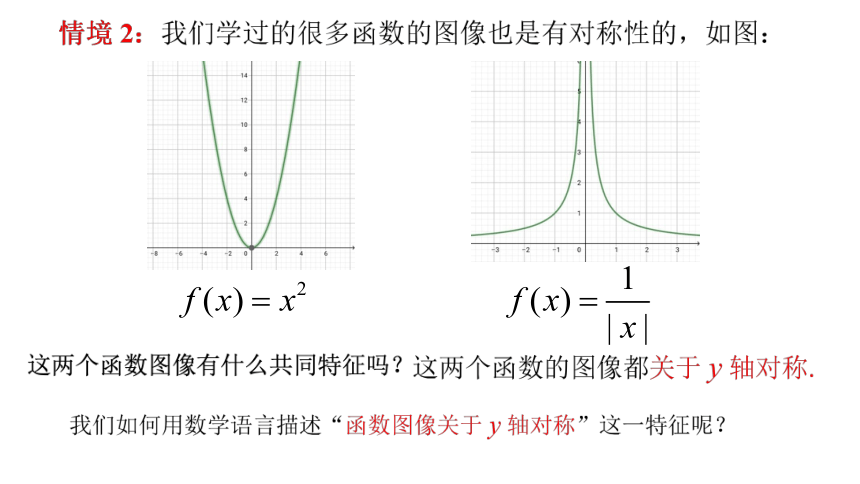
情境引入
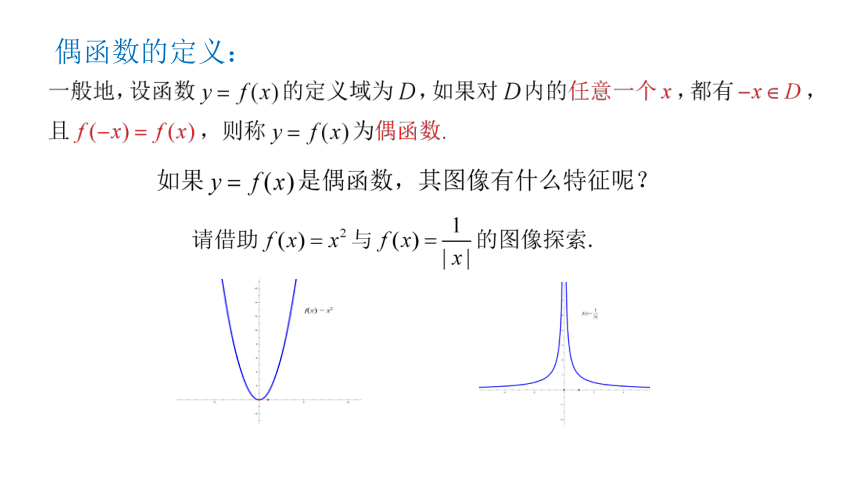
偶函数的定义:
图像1
图像2
数形结合的思想方法
观察这两个函数图像的共同特征,并尝试把奇函数的定义补充完整,同时说出奇函数图像应该具有的特征.
数形结合的思想方法
如果一个函数是
偶函数或是奇函数,则称这个函数具有奇偶性.
结合偶函数和奇函数的定义,请思考:
1.你能说出应用定义判定函数的奇偶性时,应该注意哪些问题吗?
2. “数学上认为,所谓的对称,是在运动变换下不变的一种特性”.你有什么体会?请结合函数的奇偶性,以及图像的特点谈谈你的看法.
典型例题:
奇函数
偶函数
典型例题:
奇函数
偶函数
非奇非偶
非奇非偶
(1)奇函数
(2)偶函数
(3)既不是奇函数也不是偶函数
(4)既是奇函数也是偶函数
奇函数
偶函数
非奇非偶
非奇非偶
分类与整合的思想方法
由此可见,不是所有的函数都具有奇偶性.
像(3)与(4)这样的函数,前者是定义域不符合奇偶性的定义,
后者是对应关系不符合奇偶性的定义.
奇函数
偶函数
非奇非偶
非奇非偶
BCD
AB
课堂小结
同学们再见
14
12
10
8
6
4
2
-8
-6-4
-20
2
4
6
3
2
1
32
-10
2
3
16
14
x)=x2
12-
10
-20
-15
-10
15
-2
X
4
-2
1
-21
9
nx)=x2
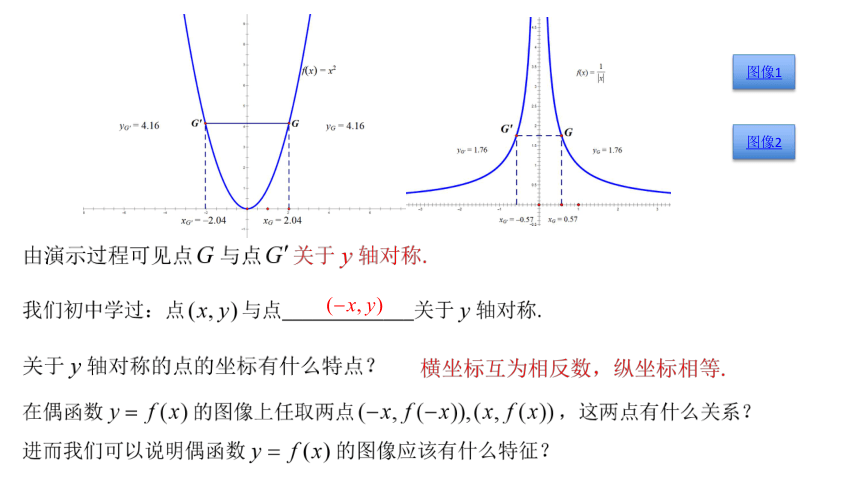
yG=4.16
G
4十
G
yG=4.16
2
-10
2
xG=-2.04
xG=2.04
4.5
3.5
fx)=
2.5
G
G
1.5
yc=1.76
yc=1.76
1
0.5
-3
1
xG=-0.57
xc=0.57
-05
-1
-15
y
(-x,g(x)/
(x,g(x))
(-x,f(x)
1
(x,f(x))
1
x
1
(x,f(x))
1
(x,f(x))
(-x,-f(x)
1
X
(-x,-f(x)
人教B版教材必修第一册
函数的奇偶性
情境引入
偶函数的定义:
图像1
图像2
数形结合的思想方法
观察这两个函数图像的共同特征,并尝试把奇函数的定义补充完整,同时说出奇函数图像应该具有的特征.
数形结合的思想方法
如果一个函数是
偶函数或是奇函数,则称这个函数具有奇偶性.
结合偶函数和奇函数的定义,请思考:
1.你能说出应用定义判定函数的奇偶性时,应该注意哪些问题吗?
2. “数学上认为,所谓的对称,是在运动变换下不变的一种特性”.你有什么体会?请结合函数的奇偶性,以及图像的特点谈谈你的看法.
典型例题:
奇函数
偶函数
典型例题:
奇函数
偶函数
非奇非偶
非奇非偶
(1)奇函数
(2)偶函数
(3)既不是奇函数也不是偶函数
(4)既是奇函数也是偶函数
奇函数
偶函数
非奇非偶
非奇非偶
分类与整合的思想方法
由此可见,不是所有的函数都具有奇偶性.
像(3)与(4)这样的函数,前者是定义域不符合奇偶性的定义,
后者是对应关系不符合奇偶性的定义.
奇函数
偶函数
非奇非偶
非奇非偶
BCD
AB
课堂小结
同学们再见
14
12
10
8
6
4
2
-8
-6-4
-20
2
4
6
3
2
1
32
-10
2
3
16
14
x)=x2
12-
10
-20
-15
-10
15
-2
X
4
-2
1
-21
9
nx)=x2
yG=4.16
G
4十
G
yG=4.16
2
-10
2
xG=-2.04
xG=2.04
4.5
3.5
fx)=
2.5
G
G
1.5
yc=1.76
yc=1.76
1
0.5
-3
1
xG=-0.57
xc=0.57
-05
-1
-15
y
(-x,g(x)/
(x,g(x))
(-x,f(x)
1
(x,f(x))
1
x
1
(x,f(x))
1
(x,f(x))
(-x,-f(x)
1
X
(-x,-f(x)
