人教A版(2019)选择性必修第三册 6.2.1排列 课件(共21张PPT)
文档属性
| 名称 | 人教A版(2019)选择性必修第三册 6.2.1排列 课件(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 809.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-24 00:00:00 | ||
图片预览








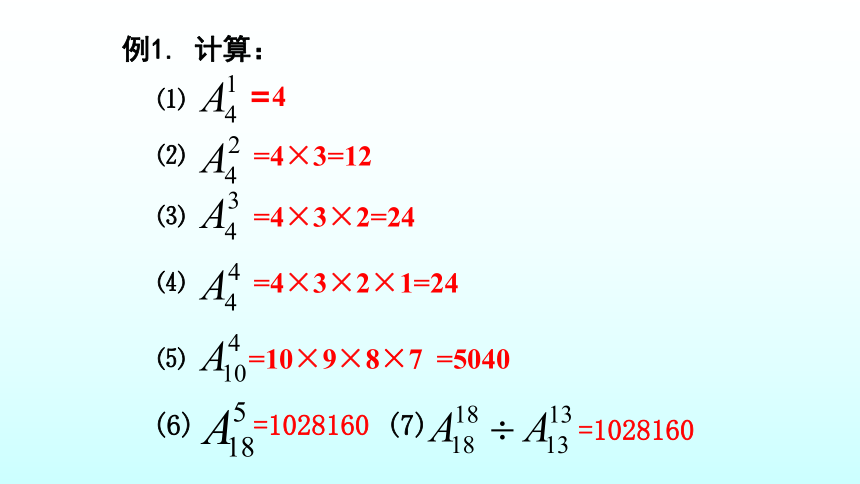
文档简介
(共21张PPT)
6.2.1 排列
N=m1+m2+…+mn
1.分类加法计数原理(分类相加)
2.分步乘法计数原理(分步相乘)
N=m1×m2×…×mn
探究:
问题1:从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学参加上午的活动,另一名同学参加下午的活动,有多少种不同的选法?
问题2:从4个不同的元素a,b,c,d中取出3个元素,按顺序排成一列,共有多少种不同的排法?
上面两个问题有什么共同特征?可以用怎样的数学模型来刻画?
基本概念
1、排列
一般地,从n个不同元素中取出m (m≤n)个元素,并按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列。
说明:
1、元素不能重复。n个中不能重复,m个中也不能重复。
2、“按一定顺序”就是与位置有关,这是判断一个问题是否是排列问题的关键。
3、两个排列相同,当且仅当这两个排列中的元素完全相同,而且元素的排列顺序也完全相同。
4、m<n时的排列叫选排列,m=n时的排列叫全排列。
5、为了使写出的所有排列情况既不重复也不遗漏,可以采用“树状图”。
例1 下列问题中哪些是排列问题?
(1)10名学生中抽2名学生开会
(2)10名学生中选2名做正、副组长
(3)从2,3,5,7,11中任取两个数相乘
(4)从2,3,5,7,11中任取两个数相除
(5)20位同学互通一次电话
(6)20位同学互通一封信
(7)以圆上的10个点为端点作弦
(8)以圆上的10个点中的某一点为起点,作过另一个点的射线
2、排列数
从n个不同的元素中取出m(m≤n)个元素的所有排列的个数,叫做从n个不同的元素中取出m个元素的排列数。用符号 表示。
“排列”和“排列数”有什么区别和联系?
排列数,而不表示具体的排列。
所有排列的个数,是一个数;
“排列数”是指从
个不同元素中,任取
个元素的
所以符号
只表示
“一个排列”是指:从
个不同元素中,任取
按照一定的顺序排成一列,不是数;
个元素
问题1中是求从3个不同元素中取出2个元素的排列数,记为 ,已经算得
问题2中是求从4个不同元素中取出3个元素的排列数,记为 ,已经算出
探究:从n个不同元素中取出2个元素的排列数 是多少?
呢?
呢?
……
第1位
第2位
第3位
第m位
n种
(n-1)种
(n-2)种
(n-m+1)种
(1)排列数公式(一):
当m=n时,
正整数1到n的连乘积,叫做n的阶乘,用 表示。
n个不同元素的全排列公式:
例1. 计算:
⑴
=4
⑵
⑶
⑷
=4×3=12
=4×3×2=24
=4×3×2×1=24
⑸
=10×9×8×7
=5040
(7)
=1028160
(6)
=1028160
n=18,
2.
若 则
用排列数符号表示为
1.若
则n= ___ m=____
由n-m+1=8,得m=11
练习
(2)排列数公式(二):
说明:
1.排列数公式的第一个常用来计算,第二个常用来证明。
为了使当m=n时上面的公式也成立,规定:
2.对于 这个条件要留意,往往是解方程时的隐含条件。
例2 求证
例3 解方程(1)
(2)
x=5
2730
1
例1 某年全国足球甲级A组联赛共有14个队参加,每队要与其余各队在主、客场分别比赛一次,共进行多少场比赛?
第二课时
B
5760
例 2(1)从5本不同的书中选3本送给3名同学,每人各1本,共有多少种不同的送法?
(2)从5种不同的书中买3本送给3名同学,每人各1本,共有多少种不同的送法?
= 5×4×3= 60
被选元素可重复选取,不是排列问题!
5×5×5= 125
“从5个不同元素中选出3个并按顺序排列”
例3 用0到9这10个数字可以组成多少个没有重复数字的三位数?
特殊位置“百位”,特殊元素“0”
百位
十位
个位
法1:
法2:
百位
十位
个位
0
百位
十位
个位
0
百位
十位
个位
例3 用0到9这10个数字可以组成多少个没有重复数字的三位数?
特殊位置“百位”,特殊元素“0”
法3:
对于有限制条件的排列问题,必须遵循“特殊元素优先考虑,特殊位置优先安排”,并注意“合理分类,准确分步”,做到“不重不漏,步骤完整” ,适当考虑“正难则反” 。
练习3
用数字0、1、2、3、4、5组成没有重复数字的数
1)有多少个五位数?
2)有多少个五位数的奇数?
3)有多少个比50000大的五位数?
4) 有多少个可以被3整除的五位数?
5)按由小到大的顺序排,42130是第几个数?
第61个数是多少?
6)有多少个奇数在奇数位的五位数?
例4 某小组7人排队照相,以下各有几种不同的排法?
1)若排成两排,前排3人,后排4人;
2)若排成两排,前排3人,后排4人,甲必排在前排,乙必排在后排;
3)甲不在左端,乙不在右端;
4)甲乙不相邻;
5)甲、乙、丙均不相邻;
7)甲乙必须间隔2人;
6)甲、乙二人必须相邻;
8)甲在乙前,乙在丙前(不一定相邻)
1.特殊位置先排
练习4 6个队员排成一排进行操练,以下各有多少种不同的站法:
⑴ 队员甲不能站排头,也不能站排尾;
⑵ 队员甲乙丙要在一起;
⑶ 队员甲乙不能在一起;
⑷ 队员甲在乙左边,丙在乙右边(不一定相邻);
2.相邻问题—捆绑法
3.不相邻问题—插空法
4.m个元素有固定顺序的---除以m!
直接法
间接法
练习5
1.7名同学排成一排,其中甲、乙两人必须排在一起的不同的排法有 种。
2.由0,1,3,5,7这五个数组成无重复数字的三位数,其中是5的倍数的共有 个.
3.某天课程表要排入政治、语文、数学、物理、物理、体育、美术共六节课,如果第一节不排体育,最后一节不排数学,则不同的排课方法有
种。
4.9位同学排成三排,每排3人,其中甲不站在前排,乙不站在后排,共有 种不同排法。
5.从1,2,…,20中任选3个不同的数,使它们成等差数列,这样的等差数列有 个。
1440
21
504
166320
180
4.基本的解题方法:
(1)特殊元素,特殊位置优先安排策略
(2)相邻问题捆绑处理的策略
(3)不相邻问题插空处理的策略
小结
1.排列的定义:
2.排列数的定义:
3.有关公式:
(2)排列数公式:
6.2.1 排列
N=m1+m2+…+mn
1.分类加法计数原理(分类相加)
2.分步乘法计数原理(分步相乘)
N=m1×m2×…×mn
探究:
问题1:从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学参加上午的活动,另一名同学参加下午的活动,有多少种不同的选法?
问题2:从4个不同的元素a,b,c,d中取出3个元素,按顺序排成一列,共有多少种不同的排法?
上面两个问题有什么共同特征?可以用怎样的数学模型来刻画?
基本概念
1、排列
一般地,从n个不同元素中取出m (m≤n)个元素,并按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列。
说明:
1、元素不能重复。n个中不能重复,m个中也不能重复。
2、“按一定顺序”就是与位置有关,这是判断一个问题是否是排列问题的关键。
3、两个排列相同,当且仅当这两个排列中的元素完全相同,而且元素的排列顺序也完全相同。
4、m<n时的排列叫选排列,m=n时的排列叫全排列。
5、为了使写出的所有排列情况既不重复也不遗漏,可以采用“树状图”。
例1 下列问题中哪些是排列问题?
(1)10名学生中抽2名学生开会
(2)10名学生中选2名做正、副组长
(3)从2,3,5,7,11中任取两个数相乘
(4)从2,3,5,7,11中任取两个数相除
(5)20位同学互通一次电话
(6)20位同学互通一封信
(7)以圆上的10个点为端点作弦
(8)以圆上的10个点中的某一点为起点,作过另一个点的射线
2、排列数
从n个不同的元素中取出m(m≤n)个元素的所有排列的个数,叫做从n个不同的元素中取出m个元素的排列数。用符号 表示。
“排列”和“排列数”有什么区别和联系?
排列数,而不表示具体的排列。
所有排列的个数,是一个数;
“排列数”是指从
个不同元素中,任取
个元素的
所以符号
只表示
“一个排列”是指:从
个不同元素中,任取
按照一定的顺序排成一列,不是数;
个元素
问题1中是求从3个不同元素中取出2个元素的排列数,记为 ,已经算得
问题2中是求从4个不同元素中取出3个元素的排列数,记为 ,已经算出
探究:从n个不同元素中取出2个元素的排列数 是多少?
呢?
呢?
……
第1位
第2位
第3位
第m位
n种
(n-1)种
(n-2)种
(n-m+1)种
(1)排列数公式(一):
当m=n时,
正整数1到n的连乘积,叫做n的阶乘,用 表示。
n个不同元素的全排列公式:
例1. 计算:
⑴
=4
⑵
⑶
⑷
=4×3=12
=4×3×2=24
=4×3×2×1=24
⑸
=10×9×8×7
=5040
(7)
=1028160
(6)
=1028160
n=18,
2.
若 则
用排列数符号表示为
1.若
则n= ___ m=____
由n-m+1=8,得m=11
练习
(2)排列数公式(二):
说明:
1.排列数公式的第一个常用来计算,第二个常用来证明。
为了使当m=n时上面的公式也成立,规定:
2.对于 这个条件要留意,往往是解方程时的隐含条件。
例2 求证
例3 解方程(1)
(2)
x=5
2730
1
例1 某年全国足球甲级A组联赛共有14个队参加,每队要与其余各队在主、客场分别比赛一次,共进行多少场比赛?
第二课时
B
5760
例 2(1)从5本不同的书中选3本送给3名同学,每人各1本,共有多少种不同的送法?
(2)从5种不同的书中买3本送给3名同学,每人各1本,共有多少种不同的送法?
= 5×4×3= 60
被选元素可重复选取,不是排列问题!
5×5×5= 125
“从5个不同元素中选出3个并按顺序排列”
例3 用0到9这10个数字可以组成多少个没有重复数字的三位数?
特殊位置“百位”,特殊元素“0”
百位
十位
个位
法1:
法2:
百位
十位
个位
0
百位
十位
个位
0
百位
十位
个位
例3 用0到9这10个数字可以组成多少个没有重复数字的三位数?
特殊位置“百位”,特殊元素“0”
法3:
对于有限制条件的排列问题,必须遵循“特殊元素优先考虑,特殊位置优先安排”,并注意“合理分类,准确分步”,做到“不重不漏,步骤完整” ,适当考虑“正难则反” 。
练习3
用数字0、1、2、3、4、5组成没有重复数字的数
1)有多少个五位数?
2)有多少个五位数的奇数?
3)有多少个比50000大的五位数?
4) 有多少个可以被3整除的五位数?
5)按由小到大的顺序排,42130是第几个数?
第61个数是多少?
6)有多少个奇数在奇数位的五位数?
例4 某小组7人排队照相,以下各有几种不同的排法?
1)若排成两排,前排3人,后排4人;
2)若排成两排,前排3人,后排4人,甲必排在前排,乙必排在后排;
3)甲不在左端,乙不在右端;
4)甲乙不相邻;
5)甲、乙、丙均不相邻;
7)甲乙必须间隔2人;
6)甲、乙二人必须相邻;
8)甲在乙前,乙在丙前(不一定相邻)
1.特殊位置先排
练习4 6个队员排成一排进行操练,以下各有多少种不同的站法:
⑴ 队员甲不能站排头,也不能站排尾;
⑵ 队员甲乙丙要在一起;
⑶ 队员甲乙不能在一起;
⑷ 队员甲在乙左边,丙在乙右边(不一定相邻);
2.相邻问题—捆绑法
3.不相邻问题—插空法
4.m个元素有固定顺序的---除以m!
直接法
间接法
练习5
1.7名同学排成一排,其中甲、乙两人必须排在一起的不同的排法有 种。
2.由0,1,3,5,7这五个数组成无重复数字的三位数,其中是5的倍数的共有 个.
3.某天课程表要排入政治、语文、数学、物理、物理、体育、美术共六节课,如果第一节不排体育,最后一节不排数学,则不同的排课方法有
种。
4.9位同学排成三排,每排3人,其中甲不站在前排,乙不站在后排,共有 种不同排法。
5.从1,2,…,20中任选3个不同的数,使它们成等差数列,这样的等差数列有 个。
1440
21
504
166320
180
4.基本的解题方法:
(1)特殊元素,特殊位置优先安排策略
(2)相邻问题捆绑处理的策略
(3)不相邻问题插空处理的策略
小结
1.排列的定义:
2.排列数的定义:
3.有关公式:
(2)排列数公式:
