人教A版(2019)选择性必修 第一册第三章 圆锥曲线的方程 课件(共20张PPT)
文档属性
| 名称 | 人教A版(2019)选择性必修 第一册第三章 圆锥曲线的方程 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-24 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
圆锥曲线与方程
(章起始课)
一、提出问题
分享古希腊数学史与生活中的圆锥曲线,基于旦德林“双球模型”探究椭圆的几何特征,类比圆的研究,推导椭圆的标准方程.
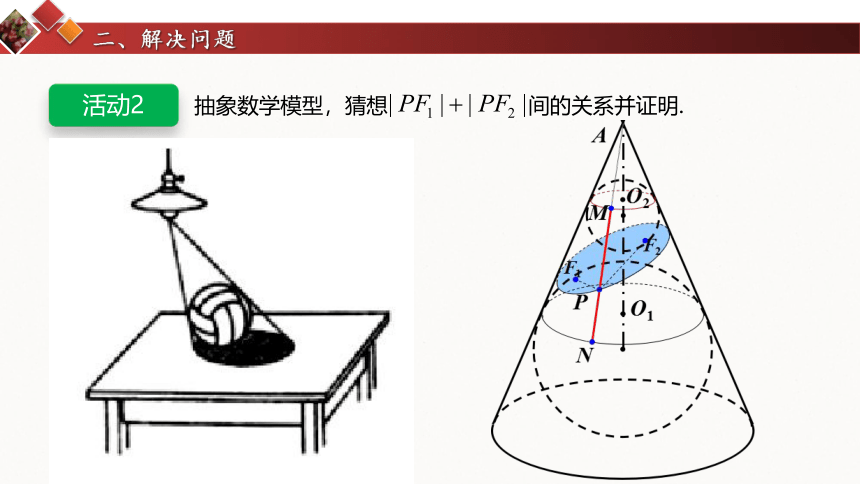
二、解决问题
活动1
简述圆锥曲线的名称由来,发展历程,发现身边的圆锥曲线.
从古至今,圆锥曲线与科研、生产、以及人类生活有着紧密的联系.其核心就是它们拥有大量的几何特征与性质.
古希腊期间,人们用纯几何的方法研究这些曲线的几何性质.但几乎每个性质的证明方法都不相同,给学习者带来了较大的困难.
二、解决问题
活动2
抽象数学模型,猜测侧面照射排球所得到的影子曲线上的点与两个切点间有着怎样的距离关系.
二、解决问题
活动2
抽象数学模型,猜想 间的关系并证明.
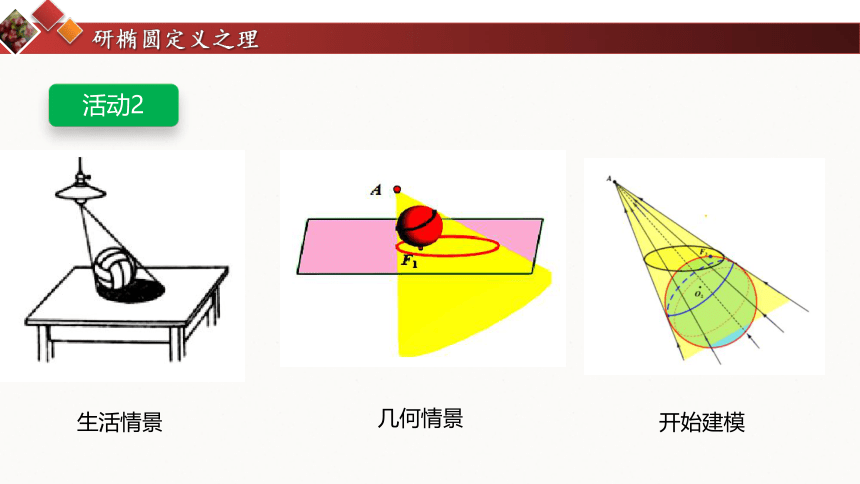
研椭圆定义之理
活动2
生活情景
几何情景
开始建模
研椭圆定义之理
问题2
模型验证
建模完成
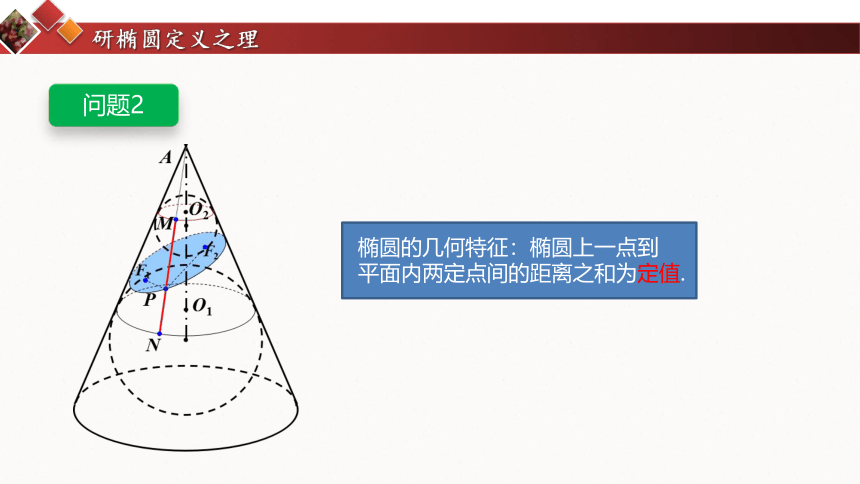
研椭圆定义之理
问题2
椭圆的几何特征:椭圆上一点到
平面内两定点间的距离之和为定值.
实验操作
根据过去利用一根细绳画出圆的经验,请大家思考该如何画出椭圆.
使用这种工具和方法所得到的曲线一定是椭圆吗?
发现:常数等于两定点距离时,轨迹为线段;常数小于两定点距离时,轨迹不存在.
二、解决问题
椭圆的定义
平面内与两个定点 的距离的和等于常数(大于 )的点的轨迹叫做椭圆.把这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距.
二、解决问题
实验操作
(2)将半径为2的圆按照竖直方向压缩二分之一得到的曲线又是什么呢?
是椭圆吗?为什么?
二、解决问题
几何
代数
笛卡尔
性质
方程
由形到数
由数到形
坐 标 法
数形结合
皮耶·德·费马
二、解决问题
对普适性方法的追求
基本图形
特征量
位置关系
度量和计算
研究的主要问题
主要方法
直线、圆
点、斜率、圆心、半径
相交、相切、相离、平行、垂直
长度、角度、面积
曲线的方程、几何性质、位置关系、图形在运动变化中的不变量等
活动3
回顾必修2中圆的研究方法与内容,梳理其研究途径.
二、解决问题
坐标法
活动3
回顾必修2中圆的研究方法与内容,梳理其研究途径.
圆的几何特征
圆的定义
圆的方程
圆的性质
位置关系
x
y
二、解决问题
基本图形 你想在圆锥曲线(椭圆)中研究什么?
特征量
位置关系 度量和计算 研究的主要问题 直线、圆
点、斜率、圆心、半径
相交、相切、相离、平行、垂直
长度、角度、面积
曲线的方程、几何性质、位置关
系、图形在运动变化中的不变量等
三、反思提升
反思提升
根据今天的学习内容,在接下来的学习中你还想研究哪些问题?
三、反思提升
反思提升
数形结合
变化
方程
坐标系
坐标
生活实际
曲线
抽象
运动
点
几何特征
坐标法
四、运用检测
运用检测
将半径为2的圆按照竖直方向压缩二分之一得到的曲线又是什么呢?
作业布置
作业布置
作业布置
圆锥曲线与方程
(章起始课)
一、提出问题
分享古希腊数学史与生活中的圆锥曲线,基于旦德林“双球模型”探究椭圆的几何特征,类比圆的研究,推导椭圆的标准方程.
二、解决问题
活动1
简述圆锥曲线的名称由来,发展历程,发现身边的圆锥曲线.
从古至今,圆锥曲线与科研、生产、以及人类生活有着紧密的联系.其核心就是它们拥有大量的几何特征与性质.
古希腊期间,人们用纯几何的方法研究这些曲线的几何性质.但几乎每个性质的证明方法都不相同,给学习者带来了较大的困难.
二、解决问题
活动2
抽象数学模型,猜测侧面照射排球所得到的影子曲线上的点与两个切点间有着怎样的距离关系.
二、解决问题
活动2
抽象数学模型,猜想 间的关系并证明.
研椭圆定义之理
活动2
生活情景
几何情景
开始建模
研椭圆定义之理
问题2
模型验证
建模完成
研椭圆定义之理
问题2
椭圆的几何特征:椭圆上一点到
平面内两定点间的距离之和为定值.
实验操作
根据过去利用一根细绳画出圆的经验,请大家思考该如何画出椭圆.
使用这种工具和方法所得到的曲线一定是椭圆吗?
发现:常数等于两定点距离时,轨迹为线段;常数小于两定点距离时,轨迹不存在.
二、解决问题
椭圆的定义
平面内与两个定点 的距离的和等于常数(大于 )的点的轨迹叫做椭圆.把这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距.
二、解决问题
实验操作
(2)将半径为2的圆按照竖直方向压缩二分之一得到的曲线又是什么呢?
是椭圆吗?为什么?
二、解决问题
几何
代数
笛卡尔
性质
方程
由形到数
由数到形
坐 标 法
数形结合
皮耶·德·费马
二、解决问题
对普适性方法的追求
基本图形
特征量
位置关系
度量和计算
研究的主要问题
主要方法
直线、圆
点、斜率、圆心、半径
相交、相切、相离、平行、垂直
长度、角度、面积
曲线的方程、几何性质、位置关系、图形在运动变化中的不变量等
活动3
回顾必修2中圆的研究方法与内容,梳理其研究途径.
二、解决问题
坐标法
活动3
回顾必修2中圆的研究方法与内容,梳理其研究途径.
圆的几何特征
圆的定义
圆的方程
圆的性质
位置关系
x
y
二、解决问题
基本图形 你想在圆锥曲线(椭圆)中研究什么?
特征量
位置关系 度量和计算 研究的主要问题 直线、圆
点、斜率、圆心、半径
相交、相切、相离、平行、垂直
长度、角度、面积
曲线的方程、几何性质、位置关
系、图形在运动变化中的不变量等
三、反思提升
反思提升
根据今天的学习内容,在接下来的学习中你还想研究哪些问题?
三、反思提升
反思提升
数形结合
变化
方程
坐标系
坐标
生活实际
曲线
抽象
运动
点
几何特征
坐标法
四、运用检测
运用检测
将半径为2的圆按照竖直方向压缩二分之一得到的曲线又是什么呢?
作业布置
作业布置
作业布置
