人教A版(2019)选择性必修第一册 3.1.1 椭圆及其标准方程课件(共17张PPT)
文档属性
| 名称 | 人教A版(2019)选择性必修第一册 3.1.1 椭圆及其标准方程课件(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-24 17:31:22 | ||
图片预览






文档简介
(共17张PPT)
——椭圆及其标准方程
创设情景,提出问题
“神舟十号”的发射及运行轨道
天体的运行
创设情景,提出问题
如何精确地设计、制作、建造出现实生活中这些椭圆形的物件呢?
生活中的椭圆
自主学习 合作探究
一 、小组合作完成绘制椭圆,
并探究椭圆的定义。
椭圆的定义
新课
平面内与两个定点 的距离和等于常数(大于 )的点的轨迹叫作椭圆,这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距 .
注意:椭圆定义中容易遗漏的三处地方:
(1) 必须在平面内;
(2)两个定点---两点间距离确定;(常记作2c)
(3)绳长---轨迹上任意点到两定点距离和确定.
(常记作2a, 且2a>2c)
轨迹是一条线段
轨迹不存在
若2a< 轨迹是什么呢?
若2a= 轨迹是什么呢?
椭圆的定义
新课
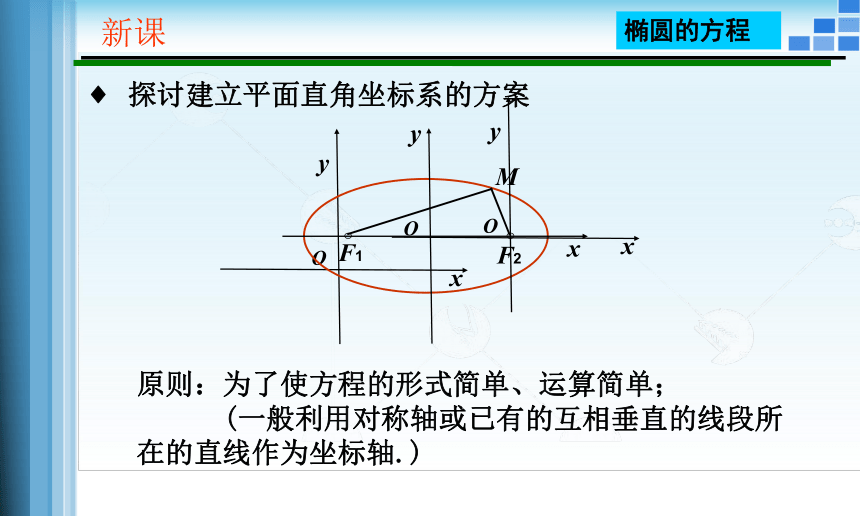
探讨建立平面直角坐标系的方案
O
x
y
M
F1
F2
原则:为了使方程的形式简单、运算简单;
(一般利用对称轴或已有的互相垂直的线段所在的直线作为坐标轴.)
椭圆的方程
O
x
y
O
x
y
新课
解:以过焦点F1、F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系(如图).
设M(x, y)是椭圆上任意一点,椭圆的焦距2c(c>0),则F1、F2的坐标分别是( c,0)、(c,0) ,M与F1和F2的距离的和等于正常数2a (2a>2c) ,
x
F1
F2
M
0
y
(问题:下面怎样化简?)
由椭圆的定义得
代入坐标
椭圆的方程
二、 化简上面的方程。
自主学习 合作探究
椭圆的方程
新课
两边除以 得
由椭圆定义可知
整理得
两边再平方,得
移项,再平方
叫做椭圆的标准方程.
椭圆的方程
自主学习 合作探究
也是椭圆的标准方程。
如果椭圆的焦点在y轴上,那么椭圆的标准方程又是怎样的呢
如果椭圆的焦点在y轴上如图所示,焦点则变成
椭圆的方程
.
p
0
x
y
(0,-c)
(0, c)
焦点在y轴:
焦点在x轴:
椭圆的标准方程:
1
o
F
y
x
2
F
M
1
2
y
o
F
F
M
x
新课
椭圆的方程
图 形
标准方程
焦 点
F(±c,0)
F(0,±c)
a,b,c之间的关系
c2=a2-b2
|MF1|+|MF2|=2a (2a>2c>0)
定 义
1
2
y
o
F
F
M
x
1
o
F
y
x
2
F
M
注:
共同点:椭圆的标准方程表示的一定是焦点在坐标轴上,中心在坐标原点的椭圆;方程的左边是平方和,右边是1.
不同点: 焦点在x轴的椭圆 项分母较大.
焦点在y轴的椭圆 项分母较大.
新课
椭圆的方程
师生互动,引导点拨
例题1. 已知椭圆的方程为: ,请填空:
(1) a=__,b=__,c=__,焦点坐标为___________ ,焦距等于__.
(2)若C为椭圆上一点,F1、F2分别为椭圆的左、右焦点, 并且|CF1|=2,则|CF2|=___.
5
4
3
6
(-3,0)、(3,0)
8
师生互动,引导点拨
例题2.求适合下列条件的椭圆的标准方程:
(2)焦点为F1(0,-3),F2(0,3),且a=5;
(1)a= ,b=1,焦点在x轴上;
(3)两个焦点分别是F1(-2,0)、F2(2,0),且过P(2,3)点;
小结:求椭圆标准方程的方法(待定系数法)
①定位:确定焦点所在的坐标轴;
②定量:求a, b的值.
师生互动,引导点拨
例题3.已知方程 表示焦点在x轴 上的椭圆,则m的取值范围是 .
(0,4)
变1:已知方程 表示焦点在y轴
上的椭圆,则m的取值范围是 .
(1,2)
1 今天我们共同体验了求椭圆方程的一种方法,也就是?
小结
椭圆及其标准方程
求椭圆标准方程的方法(待定系数法)
2 今天我们共同研究两类方程,也就是?
——椭圆及其标准方程
创设情景,提出问题
“神舟十号”的发射及运行轨道
天体的运行
创设情景,提出问题
如何精确地设计、制作、建造出现实生活中这些椭圆形的物件呢?
生活中的椭圆
自主学习 合作探究
一 、小组合作完成绘制椭圆,
并探究椭圆的定义。
椭圆的定义
新课
平面内与两个定点 的距离和等于常数(大于 )的点的轨迹叫作椭圆,这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距 .
注意:椭圆定义中容易遗漏的三处地方:
(1) 必须在平面内;
(2)两个定点---两点间距离确定;(常记作2c)
(3)绳长---轨迹上任意点到两定点距离和确定.
(常记作2a, 且2a>2c)
轨迹是一条线段
轨迹不存在
若2a< 轨迹是什么呢?
若2a= 轨迹是什么呢?
椭圆的定义
新课
探讨建立平面直角坐标系的方案
O
x
y
M
F1
F2
原则:为了使方程的形式简单、运算简单;
(一般利用对称轴或已有的互相垂直的线段所在的直线作为坐标轴.)
椭圆的方程
O
x
y
O
x
y
新课
解:以过焦点F1、F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系(如图).
设M(x, y)是椭圆上任意一点,椭圆的焦距2c(c>0),则F1、F2的坐标分别是( c,0)、(c,0) ,M与F1和F2的距离的和等于正常数2a (2a>2c) ,
x
F1
F2
M
0
y
(问题:下面怎样化简?)
由椭圆的定义得
代入坐标
椭圆的方程
二、 化简上面的方程。
自主学习 合作探究
椭圆的方程
新课
两边除以 得
由椭圆定义可知
整理得
两边再平方,得
移项,再平方
叫做椭圆的标准方程.
椭圆的方程
自主学习 合作探究
也是椭圆的标准方程。
如果椭圆的焦点在y轴上,那么椭圆的标准方程又是怎样的呢
如果椭圆的焦点在y轴上如图所示,焦点则变成
椭圆的方程
.
p
0
x
y
(0,-c)
(0, c)
焦点在y轴:
焦点在x轴:
椭圆的标准方程:
1
o
F
y
x
2
F
M
1
2
y
o
F
F
M
x
新课
椭圆的方程
图 形
标准方程
焦 点
F(±c,0)
F(0,±c)
a,b,c之间的关系
c2=a2-b2
|MF1|+|MF2|=2a (2a>2c>0)
定 义
1
2
y
o
F
F
M
x
1
o
F
y
x
2
F
M
注:
共同点:椭圆的标准方程表示的一定是焦点在坐标轴上,中心在坐标原点的椭圆;方程的左边是平方和,右边是1.
不同点: 焦点在x轴的椭圆 项分母较大.
焦点在y轴的椭圆 项分母较大.
新课
椭圆的方程
师生互动,引导点拨
例题1. 已知椭圆的方程为: ,请填空:
(1) a=__,b=__,c=__,焦点坐标为___________ ,焦距等于__.
(2)若C为椭圆上一点,F1、F2分别为椭圆的左、右焦点, 并且|CF1|=2,则|CF2|=___.
5
4
3
6
(-3,0)、(3,0)
8
师生互动,引导点拨
例题2.求适合下列条件的椭圆的标准方程:
(2)焦点为F1(0,-3),F2(0,3),且a=5;
(1)a= ,b=1,焦点在x轴上;
(3)两个焦点分别是F1(-2,0)、F2(2,0),且过P(2,3)点;
小结:求椭圆标准方程的方法(待定系数法)
①定位:确定焦点所在的坐标轴;
②定量:求a, b的值.
师生互动,引导点拨
例题3.已知方程 表示焦点在x轴 上的椭圆,则m的取值范围是 .
(0,4)
变1:已知方程 表示焦点在y轴
上的椭圆,则m的取值范围是 .
(1,2)
1 今天我们共同体验了求椭圆方程的一种方法,也就是?
小结
椭圆及其标准方程
求椭圆标准方程的方法(待定系数法)
2 今天我们共同研究两类方程,也就是?
