人教A版(2019)选择性必修第一册 3.1.1 椭圆机器标准方程 课件(共21张PPT)
文档属性
| 名称 | 人教A版(2019)选择性必修第一册 3.1.1 椭圆机器标准方程 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-24 17:32:07 | ||
图片预览






文档简介
(共21张PPT)
圆锥曲线与方程起始课
了解圆锥曲线之渊源
阿波罗尼奥斯(Apollonius of Perga,约公元前262~190年),古希腊数学家.
用纯几何学的方法将圆锥曲线的性质网罗殆尽,记载于著作《圆锥曲线论》中,到现在都无人能及.
二、为什么研究圆锥曲线?
浩瀚宇宙
欣赏圆锥曲线之美妙
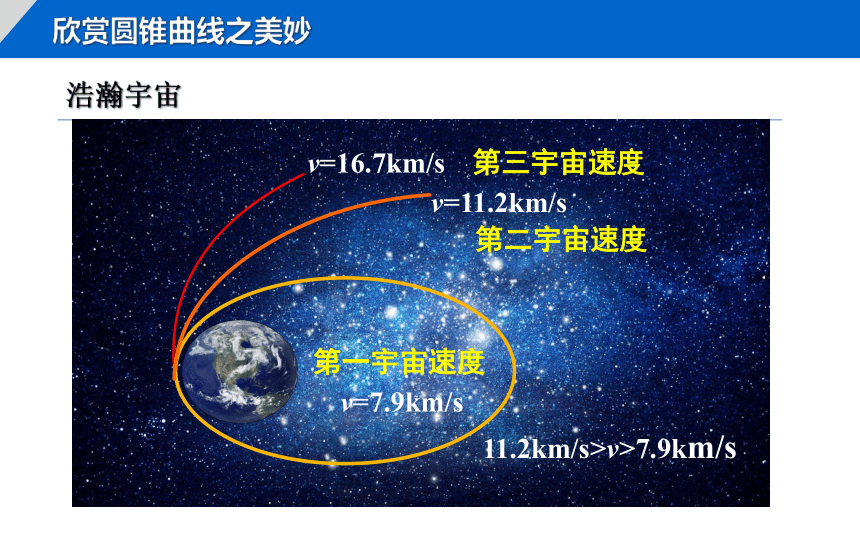
浩瀚宇宙
11.2km/s>v>7.9km/s
v=16.7km/s
第一宇宙速度
第二宇宙速度
第三宇宙速度
v=11.2km/s
v=7.9km/s
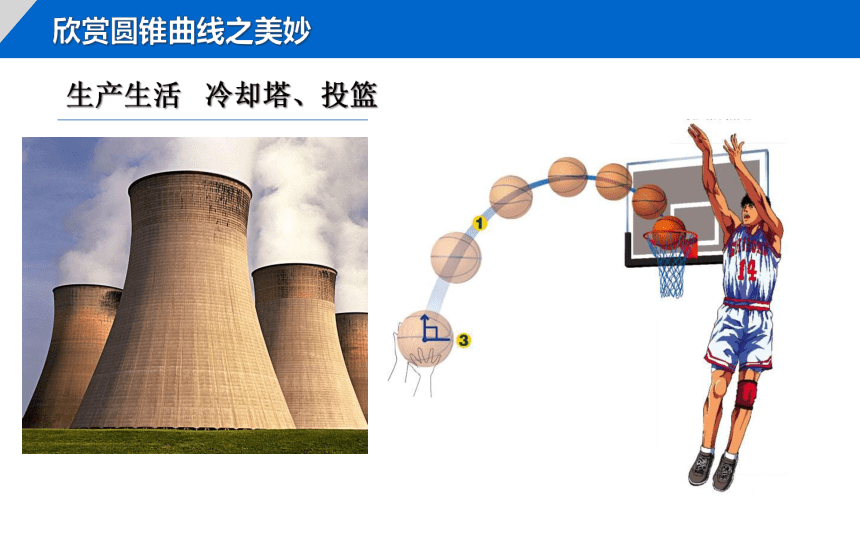
生产生活 冷却塔、投篮
欣赏圆锥曲线之美妙
科学研究 500米口径球面射电望远镜 单天线射电望远镜
欣赏圆锥曲线之美妙
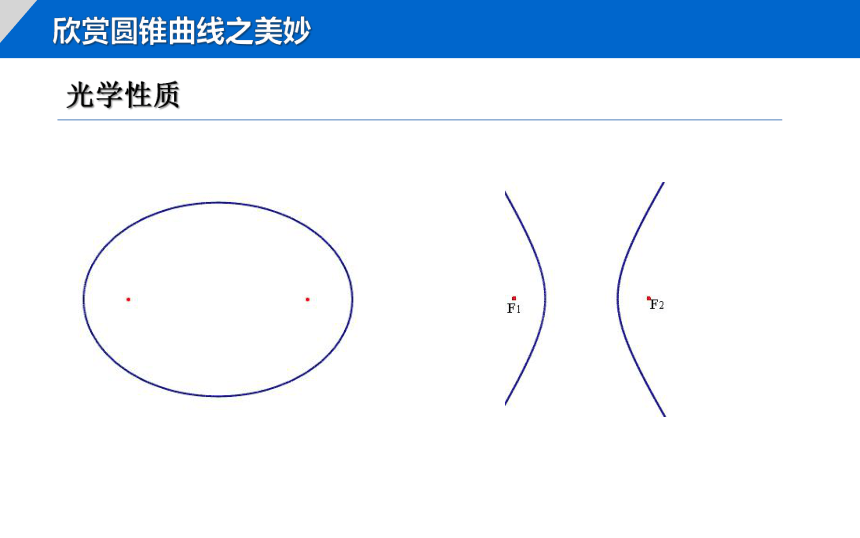
光学性质
欣赏圆锥曲线之美妙
光学性质
欣赏圆锥曲线之美妙
经典建筑
欣赏圆锥曲线之美妙
三、怎样研究圆锥曲线?
定义
方程
几何性质
坐
标
法
C
r2
笛卡尔
(公元1596年3月3日—
公元1650年2月11日)
点
(x,y)
曲线
f(x,y)=0
三、怎样研究圆锥曲线?
几何问题
代数问题
代数计算
几何性质
形
数
解析几何
坐标系
三、怎样研究圆锥曲线?
M
V
P
F1
F2
O1
O2
Q
P
M
F1
O1
F2
O2
研究圆锥曲线——椭圆
N
丹德林(Germinal Pierre Dandelin 1794年4月12-1847年2月15 比利时数学家,工程学教授)
丹德林模型中的椭圆
V
研究圆锥曲线——椭圆
Dandelin在截面的两侧分别放置一个球,使它们都与截面相切(切点分别为F1,F2),且分别与圆锥的侧面相切(两球与侧面的公共点分别构成圆O1和圆O2).如图,设点P是平面与圆锥侧面的截线上任意一点,过P点作圆锥的一条母线分别与两个球切于M,N两点.
探究一 丹德林模型中的椭圆
因为|PF1|_____|PM|
|PF2|_____|PN|
所以|PF1|+|PF2|_____|PM|+|PN|
_____|MN|
=
=
=
=
猜想 什么是椭圆?
设F1,F2为切点,P为椭圆上任一点,则
|PF1|+|PF2|=定值,
其中定值为两切点圆所截母线段的长度.
研究圆锥曲线——椭圆
思考 满足
|PF1|+|PF2|=定值
的点P的轨迹就是椭圆吗?
探究二 动手作图,验证猜想
研究圆锥曲线——椭圆
1. 请在软板上确定定点F1,F2,用笔拉紧绳子,画出点的轨迹.
2. 当|F1F2|=绳长时,用笔拉紧绳子,画出点的轨迹是
什么?
思考 椭圆上的点都满足什么条件?
椭圆的定义
平面内到两个定点F1,F2的距离的和等于常数(大于|F1F2|)
的点的轨迹叫做椭圆(ellipse),两个定点F1,F2叫做椭圆
的焦点(focus),两焦点之间的距离叫做椭圆的焦距(focal
distance).
研究圆锥曲线——椭圆
解决问题
研究圆锥曲线——椭圆
例1.在探究二中,当绳长为40,两定点间距离为30
时,请写出点的轨迹方程.
小结
什么是圆锥曲线?
为什么研究圆锥曲线?
怎样研究圆锥曲线?
坐标法
数学史
椭圆的标准方程
椭圆的定义
椭圆的性质
作业
必做题:
1.如果椭圆 上一点P到焦点F1的距离等于6,那么点P到另一个焦点F2的距离是____.
2.已知a=4,b=1,焦点在x轴上,写出椭圆的标准方程.
选做题:
查阅资料,以圆锥曲线的发展史为题,进行一篇数学写作.
课后思考
类比椭圆的定义,还可以提出什么问题?
平面内两个定点F1,F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆(ellipse),两个定点F1,F2叫做椭圆的焦点(focus),两焦点之间的距离叫做椭圆的焦距(focal distance).
圆锥曲线与方程起始课
了解圆锥曲线之渊源
阿波罗尼奥斯(Apollonius of Perga,约公元前262~190年),古希腊数学家.
用纯几何学的方法将圆锥曲线的性质网罗殆尽,记载于著作《圆锥曲线论》中,到现在都无人能及.
二、为什么研究圆锥曲线?
浩瀚宇宙
欣赏圆锥曲线之美妙
浩瀚宇宙
11.2km/s>v>7.9km/s
v=16.7km/s
第一宇宙速度
第二宇宙速度
第三宇宙速度
v=11.2km/s
v=7.9km/s
生产生活 冷却塔、投篮
欣赏圆锥曲线之美妙
科学研究 500米口径球面射电望远镜 单天线射电望远镜
欣赏圆锥曲线之美妙
光学性质
欣赏圆锥曲线之美妙
光学性质
欣赏圆锥曲线之美妙
经典建筑
欣赏圆锥曲线之美妙
三、怎样研究圆锥曲线?
定义
方程
几何性质
坐
标
法
C
r2
笛卡尔
(公元1596年3月3日—
公元1650年2月11日)
点
(x,y)
曲线
f(x,y)=0
三、怎样研究圆锥曲线?
几何问题
代数问题
代数计算
几何性质
形
数
解析几何
坐标系
三、怎样研究圆锥曲线?
M
V
P
F1
F2
O1
O2
Q
P
M
F1
O1
F2
O2
研究圆锥曲线——椭圆
N
丹德林(Germinal Pierre Dandelin 1794年4月12-1847年2月15 比利时数学家,工程学教授)
丹德林模型中的椭圆
V
研究圆锥曲线——椭圆
Dandelin在截面的两侧分别放置一个球,使它们都与截面相切(切点分别为F1,F2),且分别与圆锥的侧面相切(两球与侧面的公共点分别构成圆O1和圆O2).如图,设点P是平面与圆锥侧面的截线上任意一点,过P点作圆锥的一条母线分别与两个球切于M,N两点.
探究一 丹德林模型中的椭圆
因为|PF1|_____|PM|
|PF2|_____|PN|
所以|PF1|+|PF2|_____|PM|+|PN|
_____|MN|
=
=
=
=
猜想 什么是椭圆?
设F1,F2为切点,P为椭圆上任一点,则
|PF1|+|PF2|=定值,
其中定值为两切点圆所截母线段的长度.
研究圆锥曲线——椭圆
思考 满足
|PF1|+|PF2|=定值
的点P的轨迹就是椭圆吗?
探究二 动手作图,验证猜想
研究圆锥曲线——椭圆
1. 请在软板上确定定点F1,F2,用笔拉紧绳子,画出点的轨迹.
2. 当|F1F2|=绳长时,用笔拉紧绳子,画出点的轨迹是
什么?
思考 椭圆上的点都满足什么条件?
椭圆的定义
平面内到两个定点F1,F2的距离的和等于常数(大于|F1F2|)
的点的轨迹叫做椭圆(ellipse),两个定点F1,F2叫做椭圆
的焦点(focus),两焦点之间的距离叫做椭圆的焦距(focal
distance).
研究圆锥曲线——椭圆
解决问题
研究圆锥曲线——椭圆
例1.在探究二中,当绳长为40,两定点间距离为30
时,请写出点的轨迹方程.
小结
什么是圆锥曲线?
为什么研究圆锥曲线?
怎样研究圆锥曲线?
坐标法
数学史
椭圆的标准方程
椭圆的定义
椭圆的性质
作业
必做题:
1.如果椭圆 上一点P到焦点F1的距离等于6,那么点P到另一个焦点F2的距离是____.
2.已知a=4,b=1,焦点在x轴上,写出椭圆的标准方程.
选做题:
查阅资料,以圆锥曲线的发展史为题,进行一篇数学写作.
课后思考
类比椭圆的定义,还可以提出什么问题?
平面内两个定点F1,F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆(ellipse),两个定点F1,F2叫做椭圆的焦点(focus),两焦点之间的距离叫做椭圆的焦距(focal distance).
