圆锥曲线起始课 课件(共19张PPT)
图片预览






文档简介
(共19张PPT)
圆锥曲线起始课
——椭圆及其标准方程
椭圆的定义是什么?
椭圆有哪些性质?
椭圆又有哪些应用?
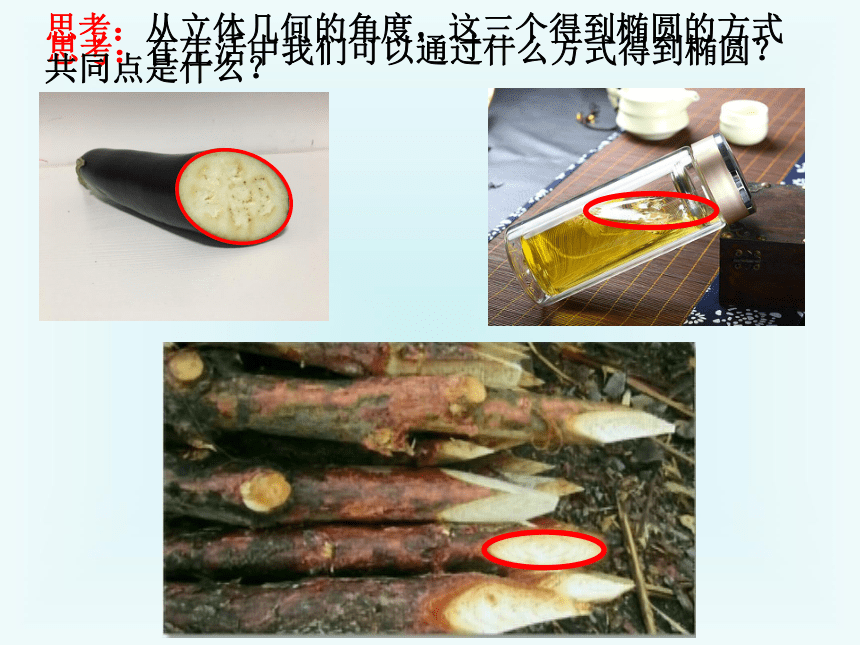
思考:在生活中我们可以通过什么方式得到椭圆?
思考:从立体几何的角度,这三个得到椭圆的方式共同点是什么?
平面斜截圆柱得到的交线为椭圆
阿波罗尼奥斯发现通过改变平面的倾斜角度去截圆锥能得到不同的曲线,并把它们命名为椭圆、双曲线、抛物线,这些曲线被统称为圆锥曲线.
阿波罗尼奥斯 (公元前262-190)
阿波罗尼奥斯用纯几何的方法研究了圆锥曲线的性质,著有《圆锥曲线论》,将圆锥曲线的几何性质几乎网罗殆尽,以致于以后的两千多年几何学裹足不前.
直到17世纪,解析几何的诞生为研究几何问题开启了一个新的思路.
笛卡尔
1596——1650
费马
1601——1665
解析几何的两位创始人
平面解析几何
借助平面直角坐标系建立了几何与代数之间的联系,并通过代数的方法研究几何图形的性质.
点 ——
求曲线方程的一般步骤:
1.建系:建立适当的直角坐标系
2.设点:设曲线上任意一点为(x, y)
3.列式:根据曲线上点所满足的数量关系条件写出等式
4.化简:用坐标(x, y)表示这个等式,并化简
椭圆上的点满足怎样的数量关系呢?
曲线 ——
坐标
方程
5.检验:方程的解构成的坐标与曲线上的点是否一一对应
椭圆上的任意一个点到到两个定点的距离之和为常数。
两个定点F1和F2称为椭圆的焦点
焦点间的距离|F1F2|称为椭圆的焦距
椭圆的性质
数学实验:画椭圆
你能根据椭圆的性质利用以下实验材料设计一个简单的数学实验来画出椭圆吗?
实验材料:木板、图钉、细绳、铅笔
推导椭圆方程
思考:怎样建系才能使椭圆的方程简单?
O
x
y
M
F11
F22
方案一
O
x
y
方案二
F11
F22
M
建 系:
O
x
y
M
F11
F22
设 点:
椭圆上的点满足P={M||MF1|+|MF2|=2a},则2a>2c>0
设 M( x,y ),
设|F1F2|=2c,则有F1(-c,0)、F2(c,0)
列式:
化简:
则:
推导椭圆方程:
思考:观察右图,你能从中找出表示 的线段吗?
O
x
y
F1
F2
P
则①式可化为:
②
令b=
①
②
从上述推导过程中可以看到:
(1)椭圆上任意一点的坐标都满足方程②;
(2)以方程②的解为坐标的点都在椭圆上;
故称②为椭圆的标准方程.
检验:
思考:焦点在y轴上的椭圆标准方程是什么?
O
x
y
焦点在y轴
F11
F22
M
O
x
y
M
F11
F22
焦点在x轴
xy互换
椭圆的截线定义
椭圆的轨迹定义
椭圆的标准方程
旦德林球
椭圆的应用
建系推导
用代数的方法研究椭圆的几何性质
课堂小结:
在此过程中你有哪些收获和感悟?
中国国家大剧院
椭圆在建筑生活中的应用
开普勒第一定律:每一个行星沿各自的椭圆轨道环绕太阳,而太阳则处在椭圆的一个焦点上.
椭圆在天体运动中的应用
1. 教材第42页练习1、2、3、4.
2. 思考:
如果是“平面斜截圆柱”所得到的椭圆,能否类比圆锥中的“旦德林球法”说明椭圆上任意一点到两个定点的距离之和为常数?
作业:
圆锥曲线起始课
——椭圆及其标准方程
椭圆的定义是什么?
椭圆有哪些性质?
椭圆又有哪些应用?
思考:在生活中我们可以通过什么方式得到椭圆?
思考:从立体几何的角度,这三个得到椭圆的方式共同点是什么?
平面斜截圆柱得到的交线为椭圆
阿波罗尼奥斯发现通过改变平面的倾斜角度去截圆锥能得到不同的曲线,并把它们命名为椭圆、双曲线、抛物线,这些曲线被统称为圆锥曲线.
阿波罗尼奥斯 (公元前262-190)
阿波罗尼奥斯用纯几何的方法研究了圆锥曲线的性质,著有《圆锥曲线论》,将圆锥曲线的几何性质几乎网罗殆尽,以致于以后的两千多年几何学裹足不前.
直到17世纪,解析几何的诞生为研究几何问题开启了一个新的思路.
笛卡尔
1596——1650
费马
1601——1665
解析几何的两位创始人
平面解析几何
借助平面直角坐标系建立了几何与代数之间的联系,并通过代数的方法研究几何图形的性质.
点 ——
求曲线方程的一般步骤:
1.建系:建立适当的直角坐标系
2.设点:设曲线上任意一点为(x, y)
3.列式:根据曲线上点所满足的数量关系条件写出等式
4.化简:用坐标(x, y)表示这个等式,并化简
椭圆上的点满足怎样的数量关系呢?
曲线 ——
坐标
方程
5.检验:方程的解构成的坐标与曲线上的点是否一一对应
椭圆上的任意一个点到到两个定点的距离之和为常数。
两个定点F1和F2称为椭圆的焦点
焦点间的距离|F1F2|称为椭圆的焦距
椭圆的性质
数学实验:画椭圆
你能根据椭圆的性质利用以下实验材料设计一个简单的数学实验来画出椭圆吗?
实验材料:木板、图钉、细绳、铅笔
推导椭圆方程
思考:怎样建系才能使椭圆的方程简单?
O
x
y
M
F11
F22
方案一
O
x
y
方案二
F11
F22
M
建 系:
O
x
y
M
F11
F22
设 点:
椭圆上的点满足P={M||MF1|+|MF2|=2a},则2a>2c>0
设 M( x,y ),
设|F1F2|=2c,则有F1(-c,0)、F2(c,0)
列式:
化简:
则:
推导椭圆方程:
思考:观察右图,你能从中找出表示 的线段吗?
O
x
y
F1
F2
P
则①式可化为:
②
令b=
①
②
从上述推导过程中可以看到:
(1)椭圆上任意一点的坐标都满足方程②;
(2)以方程②的解为坐标的点都在椭圆上;
故称②为椭圆的标准方程.
检验:
思考:焦点在y轴上的椭圆标准方程是什么?
O
x
y
焦点在y轴
F11
F22
M
O
x
y
M
F11
F22
焦点在x轴
xy互换
椭圆的截线定义
椭圆的轨迹定义
椭圆的标准方程
旦德林球
椭圆的应用
建系推导
用代数的方法研究椭圆的几何性质
课堂小结:
在此过程中你有哪些收获和感悟?
中国国家大剧院
椭圆在建筑生活中的应用
开普勒第一定律:每一个行星沿各自的椭圆轨道环绕太阳,而太阳则处在椭圆的一个焦点上.
椭圆在天体运动中的应用
1. 教材第42页练习1、2、3、4.
2. 思考:
如果是“平面斜截圆柱”所得到的椭圆,能否类比圆锥中的“旦德林球法”说明椭圆上任意一点到两个定点的距离之和为常数?
作业:
同课章节目录
