鲁科版(2019)必修 第二册2.1 运动的合成与分解 课件(18张PPT)
文档属性
| 名称 | 鲁科版(2019)必修 第二册2.1 运动的合成与分解 课件(18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 23.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-04-23 16:10:25 | ||
图片预览






文档简介
(共18张PPT)
5.2 运动的合成与分解
一、运动的合成与分解
运动1:一个蜡块,放在玻璃管底,玻璃管水平匀速向右移动,蜡块的运动是什么样的?
运动2:一个蜡块,放在装满水的玻璃管底,蜡块的运动又是怎么样的?
运动3:一个蜡块,放在装满水的玻璃管底,同时玻璃管水平匀速向右移动蜡块的运动又是什么样的?
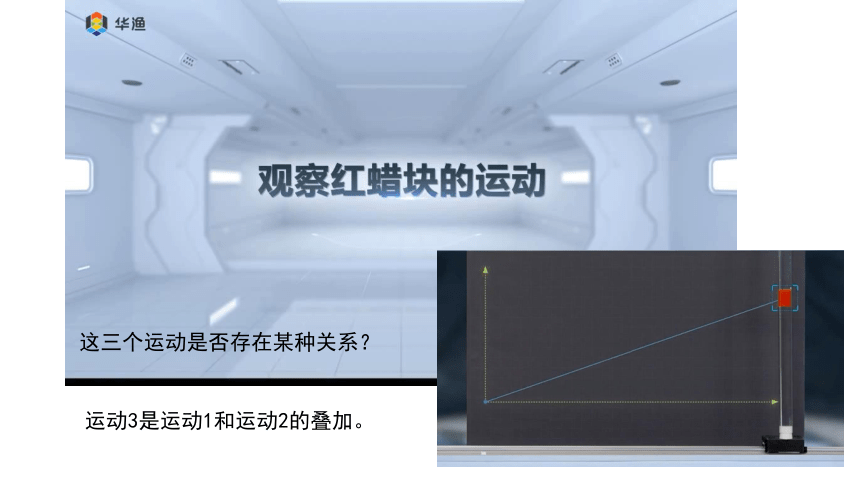
这三个运动是否存在某种关系?
这三个运动是否存在某种关系?
运动3是运动1和运动2的叠加。
如何分解?
——按照实际的运动效果来分
注意:运动(速度)的分解仍然满足平行四边形定则和三角形法则。
一个复杂的运动
两个简单的运动
二、小船渡河问题
题型特点 解题思路
①船从河岸到河对岸; ②存在水流的运动和船相对静水的运动; ③一般提问与“如何渡河时间最短”以及“如何渡河位移最短”有关。 1、以船为研究对象,画出船的运动分析图(类似于受力分析图),一般为水流的运动(确定)和船相对静水的运动(待定)两个分运动;
2、如果求“如何渡船时间最短”,则船头方向应垂直于河岸;
3、如果求“如何渡河位移最短”,则考虑两种情况:
①如果,能使船垂直过河,那么此时位移最短,根据合速度(方向垂直与河岸)确定船头方向;
②如果,合速度方向无法垂直于河岸,在这种情况下,当船头方向与合速度方向垂直时,渡河位移最短。
4、确定船相对静水的运动方向后,根据题目要求求得待求量。
【例1】一小船渡河,河宽d=180m,水流速度v1=2.5m/s.
(1)若船在静水中的速度为v2=5m/s,欲使船在最短的时间内渡河,船头应朝什么方向?用多长时间?位移是多少?
(2)若船在静水中的速度为v2=5m/s,欲使船渡河的航程最短,船头应朝什么方向?用多长时间?位移是多少?
(3)若船在静水中的速度为v2=1.5m/s,欲使船渡河的航程最短,船头应朝什么方向?用多长时间?位移是多少?
答案:(1)船头垂直于河岸;36s;
(2)船头与上游河岸成60°角;;180m
(3)船头与上游河岸成53°角;150 s;300m
【例2】河宽60m,水流速度各处相同且恒定不变,均为6m/s,小船在静水中的速度为3m/s,则:
(1)此船渡河的最短时间是多少?
(2)调整航向,可使此船渡河的航程最短,最短航程是多少?
答案:(1)20s (2)120m
【例3】如图所示,河的宽度为L,河水流速为,甲、乙两船均以相同的静水中速度同时渡河。出发时两船相距,甲、乙船头均与岸边成60°角,且乙船恰好能直达正对岸的A点。则下列判断正确的是( )
A.甲船正好也在A点靠岸
B.甲船在A点左侧靠岸
C.甲、乙两船同时到达对岸
D.甲、乙两船可能在未到达对岸前相遇
AC
三、“绳+物”问题
题型特点 解题策略
①物体由绳连接; ②物体的运动一般由绳控制; ③问题一般与物体的速度有关。 1、对物体运动进行分析,准确判断出物体的合运动(即实际运动);
2、根据运动效果合理寻找物体的分运动,一般情况下,我们这么分解运动:
①沿绳的方向——运动效果为绳的伸长或收缩
②垂直于绳的方向——运动效果为以一个点的旋转
3、画出合运动的正交分解图,并标出合运动、分运动的速度大小;
4、根据题目要求进行求解。
注:如果遇到多个用绳连接的物体系统,要牢记在绳的方向上的速度大小相等。
注:此类运动还经常用到微元法求解。
【例1】如图所示,纤绳以恒定速率v沿水平方向通过定滑轮牵引小船靠岸,当纤绳与水面夹角为时,船靠岸的速度是__________,若使船匀速靠岸,则纤绳的速度是__________(填:匀速、加速、减速)。
减速
【例2】如图所示,悬线一端固定在天花板上的O点,另一端穿过一张CD光盘的中央小孔后拴着一个橡胶球,橡胶球静止时,竖直悬线刚好挨着水平桌面的边缘。现将CD光盘按在桌面上,并沿桌面边缘以速度v匀速移动,移动过程中,CD光盘中央小孔始终紧挨桌面边线,当悬线与竖直方向的夹角为θ时,小球上升的速度大小为( )
A.
B.
C.
D.
A
【例3】如图所示,以速度v沿竖直杆匀速下滑的物体A,用细绳通过定滑轮拉动物体B在水平桌面上运动,当绳与水平面夹角为时,物体B的速率为__________。
四、“杆+物”问题
题型特点 解题策略
①物体由杆连接; ②物体的运动一般由杆控制; ③问题一般与物体的速度有关。 1、对物体运动进行分析,准确判断出物体的合运动(即实际运动);
2、根据运动效果合理寻找物体的分运动,一般情况下,我们这么分解运动:
①沿杆方向的运动
②垂直于杆方向的旋转运动
3、画出合运动的正交分解图,并标出合运动、分运动的速度大小;
4、根据题目要求进行求解。
注:如果遇到多个用杆连接的物体系统,要牢记在杆上各点沿杆的方向上的速度大小相等。
注:此类运动还经常用到微元法求解。
【例1】如图所示,滑块B以速度vB向左运动时,触电P的沿杆移动的速度如何?
【例2】一轻杆两端分别固定质量为mA和mB的两个小球A和B(可视为质点),将其放在一个光滑球形容器中从位置1开始下滑,如图所示,当轻杆到达位置2时球A与球形容器球心等高,其速度大小为v1,已知此时轻杆与水平方向成角,B球的速度大小为v2,则( )
C
【例3】如图所示,一根长直轻杆AB在墙角沿竖直墙和水平地面滑动,当AB杆和墙的夹角为θ时,杆的A端沿墙下滑的速度大小为v1,B端沿地面的速度大小为v2.则v1、v2的关系是( )
A.v1=v2
B.v1=v2cosθ
C.v1=v2tanθ
D.v1=v2sinθ
C
《练习册》P4
13、(多选)如图L5-2-9甲所示,在杂技表演中,猴子沿竖直杆向上运动,其v-t图像如图乙所示,同时人顶杆沿水平地面运动的x-t图像如图丙所示。若以地面为参考系,则下列说法中正确的是( )
A. 猴子的运动轨迹为直线
B. 猴子在前2 s内做匀变速曲线运动
C. t=0时猴子的速度大小为8 m/s
D. t=2 s时猴子的加速度大小为4 m/s2
《练习册》P4
15、如图L5-2-11所示,甲、乙两同学从河中O点出发,分别沿直线游到A点和B点后,立即沿原路线返回到O点,OA、OB分别与水流方向平行和垂直,且OA=OB。若水流速度不变,两人在静水中游速相等,则他们所用时间t甲、t乙的大小关系为 ( )
A.t甲B.t甲=t乙
C.t甲>t乙
D.无法确定
《练习册》P4
16、有一小船欲从A处渡河,如图L5-2-12所示,已知河宽为400m,其下游300m处是暗礁浅滩的危险水域,水流速度恒为5m/s,欲使小船能安全到达对岸,则船相对静水的最小速度应是多少?此时船头的指向与河岸的夹角又是多大?(sin 37°=0.6,cos 37°=0.8)
5.2 运动的合成与分解
一、运动的合成与分解
运动1:一个蜡块,放在玻璃管底,玻璃管水平匀速向右移动,蜡块的运动是什么样的?
运动2:一个蜡块,放在装满水的玻璃管底,蜡块的运动又是怎么样的?
运动3:一个蜡块,放在装满水的玻璃管底,同时玻璃管水平匀速向右移动蜡块的运动又是什么样的?
这三个运动是否存在某种关系?
这三个运动是否存在某种关系?
运动3是运动1和运动2的叠加。
如何分解?
——按照实际的运动效果来分
注意:运动(速度)的分解仍然满足平行四边形定则和三角形法则。
一个复杂的运动
两个简单的运动
二、小船渡河问题
题型特点 解题思路
①船从河岸到河对岸; ②存在水流的运动和船相对静水的运动; ③一般提问与“如何渡河时间最短”以及“如何渡河位移最短”有关。 1、以船为研究对象,画出船的运动分析图(类似于受力分析图),一般为水流的运动(确定)和船相对静水的运动(待定)两个分运动;
2、如果求“如何渡船时间最短”,则船头方向应垂直于河岸;
3、如果求“如何渡河位移最短”,则考虑两种情况:
①如果,能使船垂直过河,那么此时位移最短,根据合速度(方向垂直与河岸)确定船头方向;
②如果,合速度方向无法垂直于河岸,在这种情况下,当船头方向与合速度方向垂直时,渡河位移最短。
4、确定船相对静水的运动方向后,根据题目要求求得待求量。
【例1】一小船渡河,河宽d=180m,水流速度v1=2.5m/s.
(1)若船在静水中的速度为v2=5m/s,欲使船在最短的时间内渡河,船头应朝什么方向?用多长时间?位移是多少?
(2)若船在静水中的速度为v2=5m/s,欲使船渡河的航程最短,船头应朝什么方向?用多长时间?位移是多少?
(3)若船在静水中的速度为v2=1.5m/s,欲使船渡河的航程最短,船头应朝什么方向?用多长时间?位移是多少?
答案:(1)船头垂直于河岸;36s;
(2)船头与上游河岸成60°角;;180m
(3)船头与上游河岸成53°角;150 s;300m
【例2】河宽60m,水流速度各处相同且恒定不变,均为6m/s,小船在静水中的速度为3m/s,则:
(1)此船渡河的最短时间是多少?
(2)调整航向,可使此船渡河的航程最短,最短航程是多少?
答案:(1)20s (2)120m
【例3】如图所示,河的宽度为L,河水流速为,甲、乙两船均以相同的静水中速度同时渡河。出发时两船相距,甲、乙船头均与岸边成60°角,且乙船恰好能直达正对岸的A点。则下列判断正确的是( )
A.甲船正好也在A点靠岸
B.甲船在A点左侧靠岸
C.甲、乙两船同时到达对岸
D.甲、乙两船可能在未到达对岸前相遇
AC
三、“绳+物”问题
题型特点 解题策略
①物体由绳连接; ②物体的运动一般由绳控制; ③问题一般与物体的速度有关。 1、对物体运动进行分析,准确判断出物体的合运动(即实际运动);
2、根据运动效果合理寻找物体的分运动,一般情况下,我们这么分解运动:
①沿绳的方向——运动效果为绳的伸长或收缩
②垂直于绳的方向——运动效果为以一个点的旋转
3、画出合运动的正交分解图,并标出合运动、分运动的速度大小;
4、根据题目要求进行求解。
注:如果遇到多个用绳连接的物体系统,要牢记在绳的方向上的速度大小相等。
注:此类运动还经常用到微元法求解。
【例1】如图所示,纤绳以恒定速率v沿水平方向通过定滑轮牵引小船靠岸,当纤绳与水面夹角为时,船靠岸的速度是__________,若使船匀速靠岸,则纤绳的速度是__________(填:匀速、加速、减速)。
减速
【例2】如图所示,悬线一端固定在天花板上的O点,另一端穿过一张CD光盘的中央小孔后拴着一个橡胶球,橡胶球静止时,竖直悬线刚好挨着水平桌面的边缘。现将CD光盘按在桌面上,并沿桌面边缘以速度v匀速移动,移动过程中,CD光盘中央小孔始终紧挨桌面边线,当悬线与竖直方向的夹角为θ时,小球上升的速度大小为( )
A.
B.
C.
D.
A
【例3】如图所示,以速度v沿竖直杆匀速下滑的物体A,用细绳通过定滑轮拉动物体B在水平桌面上运动,当绳与水平面夹角为时,物体B的速率为__________。
四、“杆+物”问题
题型特点 解题策略
①物体由杆连接; ②物体的运动一般由杆控制; ③问题一般与物体的速度有关。 1、对物体运动进行分析,准确判断出物体的合运动(即实际运动);
2、根据运动效果合理寻找物体的分运动,一般情况下,我们这么分解运动:
①沿杆方向的运动
②垂直于杆方向的旋转运动
3、画出合运动的正交分解图,并标出合运动、分运动的速度大小;
4、根据题目要求进行求解。
注:如果遇到多个用杆连接的物体系统,要牢记在杆上各点沿杆的方向上的速度大小相等。
注:此类运动还经常用到微元法求解。
【例1】如图所示,滑块B以速度vB向左运动时,触电P的沿杆移动的速度如何?
【例2】一轻杆两端分别固定质量为mA和mB的两个小球A和B(可视为质点),将其放在一个光滑球形容器中从位置1开始下滑,如图所示,当轻杆到达位置2时球A与球形容器球心等高,其速度大小为v1,已知此时轻杆与水平方向成角,B球的速度大小为v2,则( )
C
【例3】如图所示,一根长直轻杆AB在墙角沿竖直墙和水平地面滑动,当AB杆和墙的夹角为θ时,杆的A端沿墙下滑的速度大小为v1,B端沿地面的速度大小为v2.则v1、v2的关系是( )
A.v1=v2
B.v1=v2cosθ
C.v1=v2tanθ
D.v1=v2sinθ
C
《练习册》P4
13、(多选)如图L5-2-9甲所示,在杂技表演中,猴子沿竖直杆向上运动,其v-t图像如图乙所示,同时人顶杆沿水平地面运动的x-t图像如图丙所示。若以地面为参考系,则下列说法中正确的是( )
A. 猴子的运动轨迹为直线
B. 猴子在前2 s内做匀变速曲线运动
C. t=0时猴子的速度大小为8 m/s
D. t=2 s时猴子的加速度大小为4 m/s2
《练习册》P4
15、如图L5-2-11所示,甲、乙两同学从河中O点出发,分别沿直线游到A点和B点后,立即沿原路线返回到O点,OA、OB分别与水流方向平行和垂直,且OA=OB。若水流速度不变,两人在静水中游速相等,则他们所用时间t甲、t乙的大小关系为 ( )
A.t甲
C.t甲>t乙
D.无法确定
《练习册》P4
16、有一小船欲从A处渡河,如图L5-2-12所示,已知河宽为400m,其下游300m处是暗礁浅滩的危险水域,水流速度恒为5m/s,欲使小船能安全到达对岸,则船相对静水的最小速度应是多少?此时船头的指向与河岸的夹角又是多大?(sin 37°=0.6,cos 37°=0.8)
同课章节目录
- 第1章 功和机械能
- 导入 神奇之能
- 第1节 机械功
- 第2节 功率
- 第3节 动能和动能定理
- 第4节 势能及其改变
- 第5节 科学验证:机械能守恒定律
- 第2章 抛体运动
- 导入 更准、更远
- 第1节 运动的合成与分解
- 第2节 平抛运动
- 第3节 科学探究:平抛运动的特点
- 第4节 生活中的抛体运动
- 第3章 圆周运动
- 导入 生活中的圆周运动
- 第1节 匀速圆周运动快慢的描述
- 第2节 科学探究:向心力
- 第3节 离心现象
- 第4章 万有引力定律及航天
- 导入 从嫦娥奔月到“阿波罗”上天
- 第2节 万有引力定律的应用
- 第3节 人类对太空的不懈探索
- 第5章 科学进步无止境
- 导入 再次跨越时空的对话
- 第1节 初识相对论
- 第2节 相对论中的神奇时空
- 第3节 探索宇宙的奥秘
