人教版六年级下学期数学数与代数—数的认识课件(共53张PPT)
文档属性
| 名称 | 人教版六年级下学期数学数与代数—数的认识课件(共53张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 13.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-23 00:00:00 | ||
图片预览











文档简介
(共53张PPT)
北师大版小学数学六年级下册
数与代数总复习
(一)数的认识
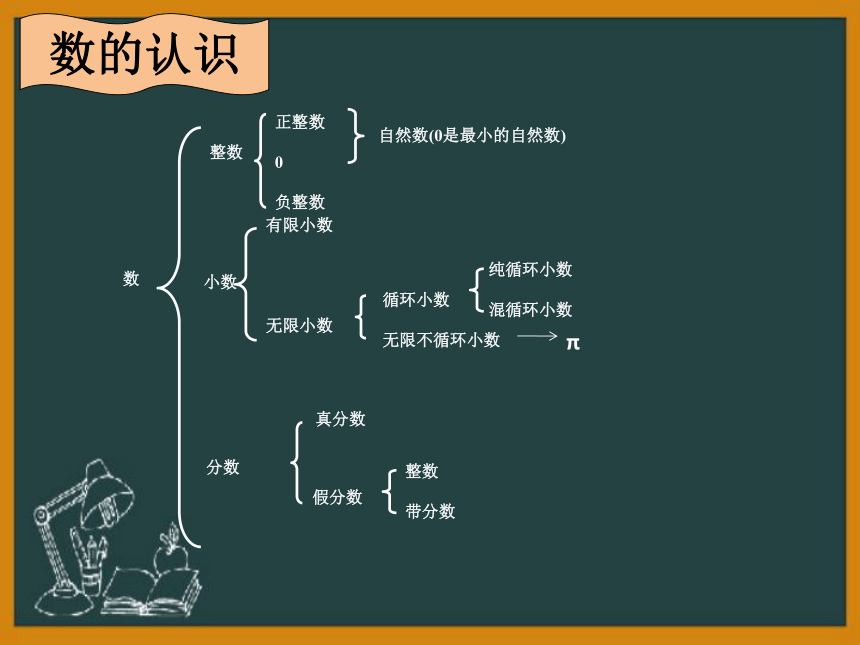
数的认识
小数,分数,百分数
整 数
因数和倍数
数的认识
正整数
0
负整数
自然数(0是最小的自然数)
有限小数
无限小数
循环小数
无限不循环小数
纯循环小数
混循环小数
假分数
整数
带分数
真分数
小数
分数
整数
数
π
你能说出下面数轴上面的数吗?你还能在数轴上表示出其他的数吗?
1、请你找出—0.5。
2、请你找出1.3。
3、请问+32是否在数轴上?
你能说一说,下图都涉及了哪一些我们学习过的知识点吗?
正整数
零
分数
正负数
1、填空。
(1)-9,5,0,1,-2,+10都是整数,其中自然数有( )个,最小的自然数是( )。
(2)像1,+2,5,6,2.5这样的数叫作( ) 数;像-3,-5,-12,-1.8这样的数叫作( )数,( )既不是正数也不是负数。
(3) 0,3,2012,176,321这些都是( )数,也是( )数。
(4)-5,-3.8,-3 ,-2,- 0, ,2,3.2,4 ,5以上各数中,整数有( )个,分数有( ),自然数有( ),正数有( ),负数有( ),正整数有( )。
1
3
3
4
1
4
1
2
4
0
正
负
0
整
自然
5
4
3
5
5
2
2、判断。
(1)“12℃”和-12℃”是表示意义相反的两个量。( )
(2)如果把向南的数记作负数,那么向西走的数就记作正数。 ( )
(3)自然数就是整数,整数就是自然数。 ( )
(4)比2小的自然数只有1个。 ( )
(5)整数包括正整数和负整数。( )
√
×
×
×
×
整 数
1、整数的意义:像-3,-2,-1,0,1,2, ……这样的数称为整数。整数中大于零的数称为正整数,小于零的数称为负整数。正整数、零和负整数统称为整数。
2、自然数的定义:我们在数物体的时候,用来表示物体个数的0,1,2,3,4,5,…叫作自然数,0也是自然数,表示一个物体也没有。
3、自然数的基本单位:任何非“0”自然数都是由若干个“一”组成的,所以“一”是自然数的基本单位。
4、“0”的含义:一个物体也没有,用“0”表示。“0”还有多方面的含义,比如在表示温度时,它是零上温度和零下温度的分界线;在刻度尺上,它是起点;在数轴上,它是正数和负数的分界点;在计数中,“0”起占位作用;还可以从运算的角度认识“0”,如任何数加0都等于原数;0和任何数相乘都得0;0 不能作除数……
注:“0”是最小的自然数,但不是最小的一位数,在自然数中,最小的一位数是“1”
5、基数与序数:表示物体有多少个的数叫基数,表示物体位于第几个(排序)的数叫序数。例如:6个小朋友赛跑,淘气跑了第6名。第一个“6”是基数,表示6个;第二个“6”是序数,表示第6。
6、整数的读法:从高位起,一级一级地读,每一级末尾的0都不读,其他数位有一个0或连续几个0,都只读一个零。读数前通常先把这个数分级,再按照各数级来读。
7、 整数的写法:从高位起,一级一级地写,哪一个数位上一个计数单位也没有就在那个数位上写0占位。
8、整数的大小比较:比较两个数的大小,先看位数,位数多的那个数就大;位数相同,从最高位比起,最高位上的数大的那个数就大,如果最高位的数相同,就比较下一位上的数……以此类推,直到比较出两个数的大小为止。
9、整数的改写:为了读写方便,常把一些较大的数改写成用“万”或“亿”作单位的数。改写时,如果是整万或整亿数,只省略万位或亿位后面的0,换一个万”或“亿”字;如果不是整万或整亿要在万位或亿位的右边点上小数点,去掉小数末尾的0,在数的后面加上“万”或“亿”字,改写后的数与原数相等,用“=”连接。
10、求整数的近似数:可以用“四舍五入”法。是“舍”还是“入”,要看省略的尾数部分的最高位上的数是小于5还是等于或大于5。省略尾数后的数与原数不相等,用 “≈”连接。
11、 一(个)、十、百、千、万……都叫做计数单位.其中“一”是计数的基本单位.
12、 10个一是十,10个十是百……10个一百亿是一千亿……每相邻两个计数单位之间的进率都是十.这种计数方法叫做十进制计数法.
1、下面的信息中有哪些数,你知道它们的具体意义吗 与同伴交流一下。
(1)第1届奥运会于1896年在希腊雅典举行,2008年在北京举行的是第29届奥运会。
(2)长江是中国第一大河,流经11个省、市、自治区。全长因6300km,流域面积因180万km。
(3)拉萨的区号为0891,面积因为31662km。历史最高气温29.6℃,最低气温零下16.5℃。2010年,常住人口因为56万。
2、填空。
(1)736054000是( )位数,它由( )个亿、( )个千万、 ( )个百万、 ( )个万、和( )个千组成。
(2) 一个九位数,最高位是最大的一位数,千万位和千 位上是8,万位和十位上是最小的质数,其余各位都是0,这个数写作( ),读作( ),改写成用 “万”作单位的数是( ),省略万位后面的尾数因 是( )
(3) 用2、7、9、6和三个0按要求组数。
①组成一个零都不读出的最大七位数。
②组成只读出一个零的最小七位数。
③组成读出两个零的七位数。
九
7
3
6
5
4
980028020
九亿八千零二万八千零二十
9800.802万
98003万
9762 000
2.000679
2070096
说一说你对0的认识
因数和倍数
公因数——最大公因数
偶数
奇数
2、3、5的倍数的特征
公倍数——最小公倍数
倍数
因数
因数和倍数
质数
合数
1
1. 整除与除尽
整除:
整数a除以整数b(b≠0),除得的商是整数而没有余数,
我们就说数a能被数b整除,或数b能整除a。
除尽:
数a除以数b(b≠0),除得的商是整数或是有限小数,
这就叫做除尽。
整除是除尽的一种特殊情况,整除也可以说是除尽,
但除尽不一定是整除。
区别:
整除
除尽
因数和倍数
2. 因数和倍数
如果数a能被数b整除(b≠0),a就叫做b的倍数,b就叫做a的因数.
因数 一个数的因数的个数是有限的,其中最小的因数是1,最大的因数是它本身。 因数和倍数是相互依存的
倍数 一个数的倍数的个数是无限的,其中最小的倍数是它本身,没有最大的倍数。
3. 能被2.3.5整除的数的特征
能被2整除的数的特征:
能被5整除的数的特征:
能被3整除的数的特征:
个位上是0,2,4,6,8,
个位上是0或5
各个位上的数字的和能被3整除
能同时被2,5整除的数的特征:
个位是0
能同时被2,3,5整除的数的特征:
个位是0,而且各个位上的
数字的和能被3整除.
注意:有一些数能被7,9,11,13整除,但是不容易看出来,
这是大家在因分中容易忽略的.
4. 偶数和奇数
一个自然数,不是奇数就是偶数
偶数:
能被2整除的数叫做偶数
奇数:
不能被2整除的数叫做奇数
偶数±偶数=( ) 奇数±奇数=( ) 偶数±奇数=( )
偶数×偶数=( ) 奇数×奇数=( ) 偶数×奇数=( )
偶数
偶数
偶数
偶数
奇数
奇数
最小的偶数是:
最小的奇数是:
0
1
5. 质数和合数
质数:
(素数)
只有1和它本身两个因数
合数:
除了1和它本身还有别的因数
1: 不是质数也不是合数
最小的质数是:
最小的合数是:
2
4
6. 质因数和分解质因数
质因数:
分解质因数:
每一个合数都可以写成几个质数相乘的形式,
这几个质数叫做这个合数的质因数.
把一个合数用几个质因数相乘的形式表示出来.
叫做分解质因数.
30
2
15
3
5
30=2×3×5
把30分解质因数正确的做法是( )
A.30=1×2 ×3 ×5
B.2 ×3 ×5=30
C.30=2×3×5
C
1不是质数
书写格式不符
把30分解质因数
分解质因数的方法:短除法
7. 最大公因数和最小公倍数
公因数,最大公因数:
几个数公有的因数,叫做这几个数的公因数;
其中最大的一个叫做这几个数的最大公因数。
例:( )是8和12的公因数,( )是8和12的最大公因数。
1,2,4
4
公倍数,最小公倍数:
几个数公有的倍数,叫做这几个数的公倍数,其中最小的一个叫做这几个数的最小公倍数。
例:( …)都是4和6的公倍数,( )是4和6的最小公倍数。
12,24,36
12
互质数:
公因数只有1的两个数叫做互质数。
⑴、两个数都是质数,这两个数一定互质。
⑵、相邻的两个数互质。
⑶、1和任何数都互质。
互质数的几种特殊情况
求最大公因数和最小公倍数
4和28 最大公因数是( );最小公倍数是( )
⑴、如果较小数是较大数的因数,那么较小数
就是这两个数的最大公因数;较大数就是这
两个数的最小公倍数。
4和15 最大公因数是( );最小公倍数是( )
⑵、如果两个数互质,它们的最大公因数就是1;
最小公倍数就是它们的积。
4
28
1
60
⑶.短除法
求24和36的最大公因数和最小公倍数
24 36
2
12
18
2
6
9
3
2
3
24和36的最大公因数是:2×2×3=12
24和36的最小公倍数是: 2×2×3×2×3=72
商互质
除数相乘
所有的除数和商相乘
分解质因数的方法如下:
(1)分解质因数法
(2)短除法
40
5
8
2
4
2
2
40
5
2
2
2
8
4
用短除法求下面数的最大公因数和最小公倍数:
45和72 32和30
45 72
3
15
24
3
5
8
24 30
2
12
15
3
4
5
二千三百零八万五千一百
2308.51
22053300
2205.33
二千四百五十四万八千二百
2454.82
50668000
5066.8
九千九百二十六万三千七百
9926.37
一、填空。
1.一个数的最小公倍数是24,这个数的因数有( )。
2.按要求在方框里填数。
(1) 两个数位上的数一样,并且是5的倍数。
(2)35 既是2的倍数,又是5的倍数。
(3)既是2的倍数,又是5的倍数的最小三位数是
3.a=2x3x5,b=2x5x11,a和b的最大公因数是( ),a和b的最小公倍数是( )。
4.两个不同质数的和是13,积是22,那么它们的差是( )。
5.(易错题)两个自然数的最大公因数是12,最小公倍数是72,这两个数是( )和( )。
二、判断。(对的画“√”,错的画“×”
1、一个数既是8的倍数,又是48的因数,这个数一定是24。 ( )
2、 两个素数的和必为合数。( )
3、 两个质数一定是互质数。( )
4、1既不是质数,也不是合数。( )
5、用2、3、0、7四个数字组成的所有四位数都能被3整除。 ( )
×
×
×
√
√
5.(1)在430097800这个数中,“3”在( )位上,万位上的数是( ),四舍五入到万位是 ( )。
(2)最小的五位数是( ),减去1是( ) ,最大的三位数加上1是( ) 。
(3)10以内的质数有( ) ,合数有( ) 。
(4)5和25的最大公因数是( ) ,5和7的最小公倍数是( ) 。
6、用 三张数字卡片按要求摆数。
(1)任意取两张数字卡片,可以摆出的2的倍数有( );可以摆出的3的倍数有( );可以摆出的5的倍数有( )。
(2)任意取两张数字卡片摆出的数中,既有因数3又有因数5的数有( )。
(3)摆出的所有三位数中,最大的是( ),最小的是( )。
7、在下面的圈里填上适当的数。
2
7
5
8、按要求填空。
9和21 11和7 28和12
最大公因数
最小公倍数
9、用短除法分解质因数。
120 68
120
5
2
2
6
24
12
2
3
68
2
2
34
17
小数,分数,百分数
1.小数
把整数“1”平均分成10份,100份……这样的一份或几份分别是十分之几,百分之几……可以用小数表示.
小数点右边第一位是十分位,计数单位是十分之一;第二位是百分位,计数单位是百分之一……
小数部分的最大计数单位是十分之一,没有最小的计数单位.
小数部分有几个数位,就叫做几位小数.
如: 记作:0.1 记作:0.08
1
1 0
8
100
2.小数的读法和写法
读小数时,小数的整数部分按整数的读法来读,小数点读作“点”,小数部分按照顺序读出每一个数位上的数字.
写小数时,整数部分按照整数的写法来写,小数点写在个位右下角,小数部分顺次写出每一个数位上的数字.
如 45.469 读作:
四十五点四六九
3.小数的性质
小数的末尾添上0或者去掉0,小数的大小不变.
运用小数的性质,可以在小数末尾添上0.
3.5=3.50
也可以把小数化简.
3.500=3.5
4.小数点数位移动引起小数大小的变化
小数点向右(左)移动一位、两位、三位……原来的数就扩大(缩小)10倍、100倍、1000倍……
如果要把一个数扩大或缩小10倍、100倍……只需要移动小数点,数位不够时用0补足.
5.循环小数
一个小数的小数部分,从某一位起,有一个或几个数字依次不断重复出现,这样的数叫做循环小数.
如 0.5555…… 7.23838……
依次不断重复出现的数字叫做循环节.
循环小数的简便记法
0.5555…… 记作:0.5
7.23838……记作:7.238
.
..
6.小数数位顺序表
整 数 部 分 小数点 小 数 部 分
…… 亿级 万级 个级
数位 …… 亿位 万位 十位 个位 . 十分位 百分位 千分位 万分位
……
计数单位 …… 亿 万 一 或个 十分之一 百分之一 千分之一 万分之一
……
一、填空
1、0.33的计数单位是( ),它有( )个这样的计数单位。
2、将0.38亿改写成用“1”作单位的数是( )。
3、甲、乙两数之和是424.2,乙数的小数点向右移动两位数就等于甲数,甲数是( )。
二、判断。(对的画“√”,错的画“x”)
1.所有的小数都比整数小。 ( )
2.因为0.58=0.580,所以它们的计数单位和意义都相同。 ( )
3. 12.3795保留三位小数是12.380。( )
4. 在5.9,6.1,6.01,5.99,6.001 中与6 最接近的数是6.001。 ( )
5.读小数和读整数一样,连续的几个0可以只读1个0。 ( )
三、解决问题
1.一个油桶可以装油100千克,装425千克油需要多少个这样的油桶?
2.制造一台机器需要1.2吨钢材,现有39吨钢材,可以制造多少台机器?
3.甲、乙两数的和是3.52,如果把甲数的小数点向右移动一位,则加、乙两数相等。甲数是多少?
1.分数的意义和分数单位
单位“1”----
一个物体,一个计量单位或是许多物体组成的一个整体,都可以用自然数1来表示,通常我们把它叫做单位“1”
分 数 ----
分数各部分的名称:
分数单位----
把单位“1”平均分成若干份,表示其中的一份的数.
7
4
分数线
分子
分母
(表示平均分的份数)
(表示所取的份数)
把单位“1”平均分成若干份,表示这样的一份或者几份的数,叫做分数.
2.分数与除法
分数与除法的关系:
被除数÷除数=
被除数
除数
(除数≠0)
a÷b=
a
b
(b≠0)
5
9
表示:
5
9
米表示:
把单位“1”平均分成9份,取其中的5份.
把5米平均分成9份,每份是( ),
每份是( )米.
1
9
5
9
3.分数大小的比较
★分母相同的两个分数,分子大的分数比较大.
★分子相同的两个分数,分母小的分数比较大.
9
1 1
1 0
1 1
8
1 5
7
1 5
4
9
4
7
11
12
5
12
<
>
<
>
★通分:先求出原来几个分母的最小公倍数,然后把各个
分数分别化成用这个最小公倍数作分母的分数.
4
6 9
1
6
=
1×9
6×9
=
9
4
9
=
4×6
9×6
=
24
<
5 4
5 4
4.分数的分类
真分数----
假分数----
分子比分母小的分数.
分子比分母大或者分子和分母相等的分数.
真分数<1
假分数≥1
5.分数的基本性质
分数的分子和分母同时乘以或者除以相同的数(零除外),分数的大小不变.
一个分数的分母不变,分子乘以3,则这个分数( )
如果分子不变,分母除以5,则这个分数( )
扩大3倍
扩大5倍
6.最简分数
*计算的结果,能因分的要因成最简分数;假分数的,一般要化成带分数或整数.
*判断一个最简分数能不能化成有限小数:
分母中除了2和5以外,不含有其他的质因数,就能化成有限小数.
4
2 5
3
4 0
7
2 0
3
8
6
13
9
1 2
2
√
√
×
√
√
√
7.约分
约分------把一个分数化成和它相等,但分子和分母都比较小的分数.
约分的方法:
1.用分子分母的公因数(1除外)逐次去除分子和分母,直到得到最简分数为止.
2.用分子和分母的最大公因数去除分子和分母.
1.一个分数约分后等于 ,已知原分数的分子、分母之差为63。求原来的分数。
2.甲用 分钟做了3个零件,乙做1个零件要 分钟,丙用1分钟做了5个零件,谁的工作效率最高
3.一个分数的分数值等于 ,分子加3,这个分数就等于自然数1,求这个分数。
4.要使 ﹤ ﹤ 成立,a可以为哪些整数
4
11
3
4
1
6
12
13
6
23
15
a
5
18
一、解决问题。
1.百分数的意义
表示一个数是另一个数的百分之几的数叫百分数.百分数又叫百分率或百分比.
百分数后面不能带单位名称。
2.百分数的读法
百分数的读法与分数相同,先读分母,再读分子。一个百分数,百分号前面的数是几,我们就把这个百分数读作“百分之几”。
3.分数、小数、百分数的互化
小数
分数
百分数
0.25=( )
小数点向右移动两位,添上%
0.35%=( )
去掉%,小数点向左移动两位
先化成小数,再化成百分数
先写成分数,再因分
先用分数表示,再因分
分子除以分母
40
100
=
40%=
2
5
1
6
≈0.167=16.7%
1
4
=0.25=25%
1.2=
25%
0.0035
2
10
1
5
1 =1
一、填空。
1.一件商品标价500元,优惠活动是“满300减100元”,这个商品实际是打( )折出售。
2.一种商品因滞销降价 20%,后来转为畅销,要恢复原价,应提价( ) %。
3.某学校植树节植树500棵,有5棵未成活,成活率是( ),读作( );死亡率是( ),读作( )。
二、判断。(对的画“√”,错的画“x”)
1.一根绳长80%米。 ( )
2.99 件商品全部合格,合格率是99%。( )
3.甲车的速度比乙车快25%,乙车的速度比甲车慢20%。 ( )
4.一种商品先打八折出售,就是现价比原价降低了80%。 ( )
三、解决问题。
1.一种商品,原价80元,现在提价10元,求售价提高了百分之几。
2. 一种电饭锅,原价100元,先提价20%出售,销量不好,又降价20%出售,电饭锅现价是多少元
3.有800克小麦,烘干后是680克,求小麦的含水率。
4.一桶汽油,第一次用去总数的30% ,第二次用去总数的 ,还剩50L,这桶汽油原来有多少升
1
5
1、读一读。(解释下面数据的具体意义)
2010年全国总用水量6022亿m,其中生活用水占12.7%,工业用水占24.0%,农业用水占61.3%,生态与环境补水(仅包括人为措施供给的城镇环境用水和部分河湖、湿地补水)占 2.0%。与2009 年比较,全国总用水量增加 56.8亿m,其中生活用水增加17.7亿㎡,工业用水增加56.4亿m,农业用水减少34.1亿m,生态与环境补水增加16.8亿㎡。
2、用分数表示图形中不同颜色的部分占整个图形的几分之几。
北师大版小学数学六年级下册
数与代数总复习
(一)数的认识
数的认识
小数,分数,百分数
整 数
因数和倍数
数的认识
正整数
0
负整数
自然数(0是最小的自然数)
有限小数
无限小数
循环小数
无限不循环小数
纯循环小数
混循环小数
假分数
整数
带分数
真分数
小数
分数
整数
数
π
你能说出下面数轴上面的数吗?你还能在数轴上表示出其他的数吗?
1、请你找出—0.5。
2、请你找出1.3。
3、请问+32是否在数轴上?
你能说一说,下图都涉及了哪一些我们学习过的知识点吗?
正整数
零
分数
正负数
1、填空。
(1)-9,5,0,1,-2,+10都是整数,其中自然数有( )个,最小的自然数是( )。
(2)像1,+2,5,6,2.5这样的数叫作( ) 数;像-3,-5,-12,-1.8这样的数叫作( )数,( )既不是正数也不是负数。
(3) 0,3,2012,176,321这些都是( )数,也是( )数。
(4)-5,-3.8,-3 ,-2,- 0, ,2,3.2,4 ,5以上各数中,整数有( )个,分数有( ),自然数有( ),正数有( ),负数有( ),正整数有( )。
1
3
3
4
1
4
1
2
4
0
正
负
0
整
自然
5
4
3
5
5
2
2、判断。
(1)“12℃”和-12℃”是表示意义相反的两个量。( )
(2)如果把向南的数记作负数,那么向西走的数就记作正数。 ( )
(3)自然数就是整数,整数就是自然数。 ( )
(4)比2小的自然数只有1个。 ( )
(5)整数包括正整数和负整数。( )
√
×
×
×
×
整 数
1、整数的意义:像-3,-2,-1,0,1,2, ……这样的数称为整数。整数中大于零的数称为正整数,小于零的数称为负整数。正整数、零和负整数统称为整数。
2、自然数的定义:我们在数物体的时候,用来表示物体个数的0,1,2,3,4,5,…叫作自然数,0也是自然数,表示一个物体也没有。
3、自然数的基本单位:任何非“0”自然数都是由若干个“一”组成的,所以“一”是自然数的基本单位。
4、“0”的含义:一个物体也没有,用“0”表示。“0”还有多方面的含义,比如在表示温度时,它是零上温度和零下温度的分界线;在刻度尺上,它是起点;在数轴上,它是正数和负数的分界点;在计数中,“0”起占位作用;还可以从运算的角度认识“0”,如任何数加0都等于原数;0和任何数相乘都得0;0 不能作除数……
注:“0”是最小的自然数,但不是最小的一位数,在自然数中,最小的一位数是“1”
5、基数与序数:表示物体有多少个的数叫基数,表示物体位于第几个(排序)的数叫序数。例如:6个小朋友赛跑,淘气跑了第6名。第一个“6”是基数,表示6个;第二个“6”是序数,表示第6。
6、整数的读法:从高位起,一级一级地读,每一级末尾的0都不读,其他数位有一个0或连续几个0,都只读一个零。读数前通常先把这个数分级,再按照各数级来读。
7、 整数的写法:从高位起,一级一级地写,哪一个数位上一个计数单位也没有就在那个数位上写0占位。
8、整数的大小比较:比较两个数的大小,先看位数,位数多的那个数就大;位数相同,从最高位比起,最高位上的数大的那个数就大,如果最高位的数相同,就比较下一位上的数……以此类推,直到比较出两个数的大小为止。
9、整数的改写:为了读写方便,常把一些较大的数改写成用“万”或“亿”作单位的数。改写时,如果是整万或整亿数,只省略万位或亿位后面的0,换一个万”或“亿”字;如果不是整万或整亿要在万位或亿位的右边点上小数点,去掉小数末尾的0,在数的后面加上“万”或“亿”字,改写后的数与原数相等,用“=”连接。
10、求整数的近似数:可以用“四舍五入”法。是“舍”还是“入”,要看省略的尾数部分的最高位上的数是小于5还是等于或大于5。省略尾数后的数与原数不相等,用 “≈”连接。
11、 一(个)、十、百、千、万……都叫做计数单位.其中“一”是计数的基本单位.
12、 10个一是十,10个十是百……10个一百亿是一千亿……每相邻两个计数单位之间的进率都是十.这种计数方法叫做十进制计数法.
1、下面的信息中有哪些数,你知道它们的具体意义吗 与同伴交流一下。
(1)第1届奥运会于1896年在希腊雅典举行,2008年在北京举行的是第29届奥运会。
(2)长江是中国第一大河,流经11个省、市、自治区。全长因6300km,流域面积因180万km。
(3)拉萨的区号为0891,面积因为31662km。历史最高气温29.6℃,最低气温零下16.5℃。2010年,常住人口因为56万。
2、填空。
(1)736054000是( )位数,它由( )个亿、( )个千万、 ( )个百万、 ( )个万、和( )个千组成。
(2) 一个九位数,最高位是最大的一位数,千万位和千 位上是8,万位和十位上是最小的质数,其余各位都是0,这个数写作( ),读作( ),改写成用 “万”作单位的数是( ),省略万位后面的尾数因 是( )
(3) 用2、7、9、6和三个0按要求组数。
①组成一个零都不读出的最大七位数。
②组成只读出一个零的最小七位数。
③组成读出两个零的七位数。
九
7
3
6
5
4
980028020
九亿八千零二万八千零二十
9800.802万
98003万
9762 000
2.000679
2070096
说一说你对0的认识
因数和倍数
公因数——最大公因数
偶数
奇数
2、3、5的倍数的特征
公倍数——最小公倍数
倍数
因数
因数和倍数
质数
合数
1
1. 整除与除尽
整除:
整数a除以整数b(b≠0),除得的商是整数而没有余数,
我们就说数a能被数b整除,或数b能整除a。
除尽:
数a除以数b(b≠0),除得的商是整数或是有限小数,
这就叫做除尽。
整除是除尽的一种特殊情况,整除也可以说是除尽,
但除尽不一定是整除。
区别:
整除
除尽
因数和倍数
2. 因数和倍数
如果数a能被数b整除(b≠0),a就叫做b的倍数,b就叫做a的因数.
因数 一个数的因数的个数是有限的,其中最小的因数是1,最大的因数是它本身。 因数和倍数是相互依存的
倍数 一个数的倍数的个数是无限的,其中最小的倍数是它本身,没有最大的倍数。
3. 能被2.3.5整除的数的特征
能被2整除的数的特征:
能被5整除的数的特征:
能被3整除的数的特征:
个位上是0,2,4,6,8,
个位上是0或5
各个位上的数字的和能被3整除
能同时被2,5整除的数的特征:
个位是0
能同时被2,3,5整除的数的特征:
个位是0,而且各个位上的
数字的和能被3整除.
注意:有一些数能被7,9,11,13整除,但是不容易看出来,
这是大家在因分中容易忽略的.
4. 偶数和奇数
一个自然数,不是奇数就是偶数
偶数:
能被2整除的数叫做偶数
奇数:
不能被2整除的数叫做奇数
偶数±偶数=( ) 奇数±奇数=( ) 偶数±奇数=( )
偶数×偶数=( ) 奇数×奇数=( ) 偶数×奇数=( )
偶数
偶数
偶数
偶数
奇数
奇数
最小的偶数是:
最小的奇数是:
0
1
5. 质数和合数
质数:
(素数)
只有1和它本身两个因数
合数:
除了1和它本身还有别的因数
1: 不是质数也不是合数
最小的质数是:
最小的合数是:
2
4
6. 质因数和分解质因数
质因数:
分解质因数:
每一个合数都可以写成几个质数相乘的形式,
这几个质数叫做这个合数的质因数.
把一个合数用几个质因数相乘的形式表示出来.
叫做分解质因数.
30
2
15
3
5
30=2×3×5
把30分解质因数正确的做法是( )
A.30=1×2 ×3 ×5
B.2 ×3 ×5=30
C.30=2×3×5
C
1不是质数
书写格式不符
把30分解质因数
分解质因数的方法:短除法
7. 最大公因数和最小公倍数
公因数,最大公因数:
几个数公有的因数,叫做这几个数的公因数;
其中最大的一个叫做这几个数的最大公因数。
例:( )是8和12的公因数,( )是8和12的最大公因数。
1,2,4
4
公倍数,最小公倍数:
几个数公有的倍数,叫做这几个数的公倍数,其中最小的一个叫做这几个数的最小公倍数。
例:( …)都是4和6的公倍数,( )是4和6的最小公倍数。
12,24,36
12
互质数:
公因数只有1的两个数叫做互质数。
⑴、两个数都是质数,这两个数一定互质。
⑵、相邻的两个数互质。
⑶、1和任何数都互质。
互质数的几种特殊情况
求最大公因数和最小公倍数
4和28 最大公因数是( );最小公倍数是( )
⑴、如果较小数是较大数的因数,那么较小数
就是这两个数的最大公因数;较大数就是这
两个数的最小公倍数。
4和15 最大公因数是( );最小公倍数是( )
⑵、如果两个数互质,它们的最大公因数就是1;
最小公倍数就是它们的积。
4
28
1
60
⑶.短除法
求24和36的最大公因数和最小公倍数
24 36
2
12
18
2
6
9
3
2
3
24和36的最大公因数是:2×2×3=12
24和36的最小公倍数是: 2×2×3×2×3=72
商互质
除数相乘
所有的除数和商相乘
分解质因数的方法如下:
(1)分解质因数法
(2)短除法
40
5
8
2
4
2
2
40
5
2
2
2
8
4
用短除法求下面数的最大公因数和最小公倍数:
45和72 32和30
45 72
3
15
24
3
5
8
24 30
2
12
15
3
4
5
二千三百零八万五千一百
2308.51
22053300
2205.33
二千四百五十四万八千二百
2454.82
50668000
5066.8
九千九百二十六万三千七百
9926.37
一、填空。
1.一个数的最小公倍数是24,这个数的因数有( )。
2.按要求在方框里填数。
(1) 两个数位上的数一样,并且是5的倍数。
(2)35 既是2的倍数,又是5的倍数。
(3)既是2的倍数,又是5的倍数的最小三位数是
3.a=2x3x5,b=2x5x11,a和b的最大公因数是( ),a和b的最小公倍数是( )。
4.两个不同质数的和是13,积是22,那么它们的差是( )。
5.(易错题)两个自然数的最大公因数是12,最小公倍数是72,这两个数是( )和( )。
二、判断。(对的画“√”,错的画“×”
1、一个数既是8的倍数,又是48的因数,这个数一定是24。 ( )
2、 两个素数的和必为合数。( )
3、 两个质数一定是互质数。( )
4、1既不是质数,也不是合数。( )
5、用2、3、0、7四个数字组成的所有四位数都能被3整除。 ( )
×
×
×
√
√
5.(1)在430097800这个数中,“3”在( )位上,万位上的数是( ),四舍五入到万位是 ( )。
(2)最小的五位数是( ),减去1是( ) ,最大的三位数加上1是( ) 。
(3)10以内的质数有( ) ,合数有( ) 。
(4)5和25的最大公因数是( ) ,5和7的最小公倍数是( ) 。
6、用 三张数字卡片按要求摆数。
(1)任意取两张数字卡片,可以摆出的2的倍数有( );可以摆出的3的倍数有( );可以摆出的5的倍数有( )。
(2)任意取两张数字卡片摆出的数中,既有因数3又有因数5的数有( )。
(3)摆出的所有三位数中,最大的是( ),最小的是( )。
7、在下面的圈里填上适当的数。
2
7
5
8、按要求填空。
9和21 11和7 28和12
最大公因数
最小公倍数
9、用短除法分解质因数。
120 68
120
5
2
2
6
24
12
2
3
68
2
2
34
17
小数,分数,百分数
1.小数
把整数“1”平均分成10份,100份……这样的一份或几份分别是十分之几,百分之几……可以用小数表示.
小数点右边第一位是十分位,计数单位是十分之一;第二位是百分位,计数单位是百分之一……
小数部分的最大计数单位是十分之一,没有最小的计数单位.
小数部分有几个数位,就叫做几位小数.
如: 记作:0.1 记作:0.08
1
1 0
8
100
2.小数的读法和写法
读小数时,小数的整数部分按整数的读法来读,小数点读作“点”,小数部分按照顺序读出每一个数位上的数字.
写小数时,整数部分按照整数的写法来写,小数点写在个位右下角,小数部分顺次写出每一个数位上的数字.
如 45.469 读作:
四十五点四六九
3.小数的性质
小数的末尾添上0或者去掉0,小数的大小不变.
运用小数的性质,可以在小数末尾添上0.
3.5=3.50
也可以把小数化简.
3.500=3.5
4.小数点数位移动引起小数大小的变化
小数点向右(左)移动一位、两位、三位……原来的数就扩大(缩小)10倍、100倍、1000倍……
如果要把一个数扩大或缩小10倍、100倍……只需要移动小数点,数位不够时用0补足.
5.循环小数
一个小数的小数部分,从某一位起,有一个或几个数字依次不断重复出现,这样的数叫做循环小数.
如 0.5555…… 7.23838……
依次不断重复出现的数字叫做循环节.
循环小数的简便记法
0.5555…… 记作:0.5
7.23838……记作:7.238
.
..
6.小数数位顺序表
整 数 部 分 小数点 小 数 部 分
…… 亿级 万级 个级
数位 …… 亿位 万位 十位 个位 . 十分位 百分位 千分位 万分位
……
计数单位 …… 亿 万 一 或个 十分之一 百分之一 千分之一 万分之一
……
一、填空
1、0.33的计数单位是( ),它有( )个这样的计数单位。
2、将0.38亿改写成用“1”作单位的数是( )。
3、甲、乙两数之和是424.2,乙数的小数点向右移动两位数就等于甲数,甲数是( )。
二、判断。(对的画“√”,错的画“x”)
1.所有的小数都比整数小。 ( )
2.因为0.58=0.580,所以它们的计数单位和意义都相同。 ( )
3. 12.3795保留三位小数是12.380。( )
4. 在5.9,6.1,6.01,5.99,6.001 中与6 最接近的数是6.001。 ( )
5.读小数和读整数一样,连续的几个0可以只读1个0。 ( )
三、解决问题
1.一个油桶可以装油100千克,装425千克油需要多少个这样的油桶?
2.制造一台机器需要1.2吨钢材,现有39吨钢材,可以制造多少台机器?
3.甲、乙两数的和是3.52,如果把甲数的小数点向右移动一位,则加、乙两数相等。甲数是多少?
1.分数的意义和分数单位
单位“1”----
一个物体,一个计量单位或是许多物体组成的一个整体,都可以用自然数1来表示,通常我们把它叫做单位“1”
分 数 ----
分数各部分的名称:
分数单位----
把单位“1”平均分成若干份,表示其中的一份的数.
7
4
分数线
分子
分母
(表示平均分的份数)
(表示所取的份数)
把单位“1”平均分成若干份,表示这样的一份或者几份的数,叫做分数.
2.分数与除法
分数与除法的关系:
被除数÷除数=
被除数
除数
(除数≠0)
a÷b=
a
b
(b≠0)
5
9
表示:
5
9
米表示:
把单位“1”平均分成9份,取其中的5份.
把5米平均分成9份,每份是( ),
每份是( )米.
1
9
5
9
3.分数大小的比较
★分母相同的两个分数,分子大的分数比较大.
★分子相同的两个分数,分母小的分数比较大.
9
1 1
1 0
1 1
8
1 5
7
1 5
4
9
4
7
11
12
5
12
<
>
<
>
★通分:先求出原来几个分母的最小公倍数,然后把各个
分数分别化成用这个最小公倍数作分母的分数.
4
6 9
1
6
=
1×9
6×9
=
9
4
9
=
4×6
9×6
=
24
<
5 4
5 4
4.分数的分类
真分数----
假分数----
分子比分母小的分数.
分子比分母大或者分子和分母相等的分数.
真分数<1
假分数≥1
5.分数的基本性质
分数的分子和分母同时乘以或者除以相同的数(零除外),分数的大小不变.
一个分数的分母不变,分子乘以3,则这个分数( )
如果分子不变,分母除以5,则这个分数( )
扩大3倍
扩大5倍
6.最简分数
*计算的结果,能因分的要因成最简分数;假分数的,一般要化成带分数或整数.
*判断一个最简分数能不能化成有限小数:
分母中除了2和5以外,不含有其他的质因数,就能化成有限小数.
4
2 5
3
4 0
7
2 0
3
8
6
13
9
1 2
2
√
√
×
√
√
√
7.约分
约分------把一个分数化成和它相等,但分子和分母都比较小的分数.
约分的方法:
1.用分子分母的公因数(1除外)逐次去除分子和分母,直到得到最简分数为止.
2.用分子和分母的最大公因数去除分子和分母.
1.一个分数约分后等于 ,已知原分数的分子、分母之差为63。求原来的分数。
2.甲用 分钟做了3个零件,乙做1个零件要 分钟,丙用1分钟做了5个零件,谁的工作效率最高
3.一个分数的分数值等于 ,分子加3,这个分数就等于自然数1,求这个分数。
4.要使 ﹤ ﹤ 成立,a可以为哪些整数
4
11
3
4
1
6
12
13
6
23
15
a
5
18
一、解决问题。
1.百分数的意义
表示一个数是另一个数的百分之几的数叫百分数.百分数又叫百分率或百分比.
百分数后面不能带单位名称。
2.百分数的读法
百分数的读法与分数相同,先读分母,再读分子。一个百分数,百分号前面的数是几,我们就把这个百分数读作“百分之几”。
3.分数、小数、百分数的互化
小数
分数
百分数
0.25=( )
小数点向右移动两位,添上%
0.35%=( )
去掉%,小数点向左移动两位
先化成小数,再化成百分数
先写成分数,再因分
先用分数表示,再因分
分子除以分母
40
100
=
40%=
2
5
1
6
≈0.167=16.7%
1
4
=0.25=25%
1.2=
25%
0.0035
2
10
1
5
1 =1
一、填空。
1.一件商品标价500元,优惠活动是“满300减100元”,这个商品实际是打( )折出售。
2.一种商品因滞销降价 20%,后来转为畅销,要恢复原价,应提价( ) %。
3.某学校植树节植树500棵,有5棵未成活,成活率是( ),读作( );死亡率是( ),读作( )。
二、判断。(对的画“√”,错的画“x”)
1.一根绳长80%米。 ( )
2.99 件商品全部合格,合格率是99%。( )
3.甲车的速度比乙车快25%,乙车的速度比甲车慢20%。 ( )
4.一种商品先打八折出售,就是现价比原价降低了80%。 ( )
三、解决问题。
1.一种商品,原价80元,现在提价10元,求售价提高了百分之几。
2. 一种电饭锅,原价100元,先提价20%出售,销量不好,又降价20%出售,电饭锅现价是多少元
3.有800克小麦,烘干后是680克,求小麦的含水率。
4.一桶汽油,第一次用去总数的30% ,第二次用去总数的 ,还剩50L,这桶汽油原来有多少升
1
5
1、读一读。(解释下面数据的具体意义)
2010年全国总用水量6022亿m,其中生活用水占12.7%,工业用水占24.0%,农业用水占61.3%,生态与环境补水(仅包括人为措施供给的城镇环境用水和部分河湖、湿地补水)占 2.0%。与2009 年比较,全国总用水量增加 56.8亿m,其中生活用水增加17.7亿㎡,工业用水增加56.4亿m,农业用水减少34.1亿m,生态与环境补水增加16.8亿㎡。
2、用分数表示图形中不同颜色的部分占整个图形的几分之几。
