沪科版数学七年级下册 6.1 平方根 、立方根 课件(共19张PPT)
文档属性
| 名称 | 沪科版数学七年级下册 6.1 平方根 、立方根 课件(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-24 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
6.1 平 方 根
不去耕耘,不去播种,再肥的沃土也长不出庄稼;
不去奋斗,不去创造,再美的青春也结不出硕果。
美国作家杰克伦敦成名后,曾收到过一位女士的求爱信:“你有一个出众的名声,我有一个高贵的地位.这两者加起来,再乘上万能的黄金,足以使我们建立起一个天堂都不能比拟的美满家庭.”
开平方的爱情公式
从这个故事中你发现哪些新的名词?
数学趣事
杰克伦敦连忙回信,他答得很妙:“根据你列出的那道爱情公式,我看还要开平方!不过这个平方根却是负数”.
为了趣味接力比赛,要在运动场上圈出一个面积为100平
方米的正方形场地,这个正方
形场地的边长为多少
10米
身边小事
因为 =100
10
2
?
小明是小学五年级的学生,他非常喜欢画画,这不学校要举行美术作品比赛,小明很高兴,但要求画布面积为50cm 的正方形。可是小明怎么也求不出画布的边长,小明非常着急,只好向上七年级的邻居小娟请教?
身边小事
小娟也犯难了,哪个数的平方是50呢?
小娟想:我还是去学校问老师吧,我一定要认真听讲,
不然不能解决小明的问题,那也太丢面子了。
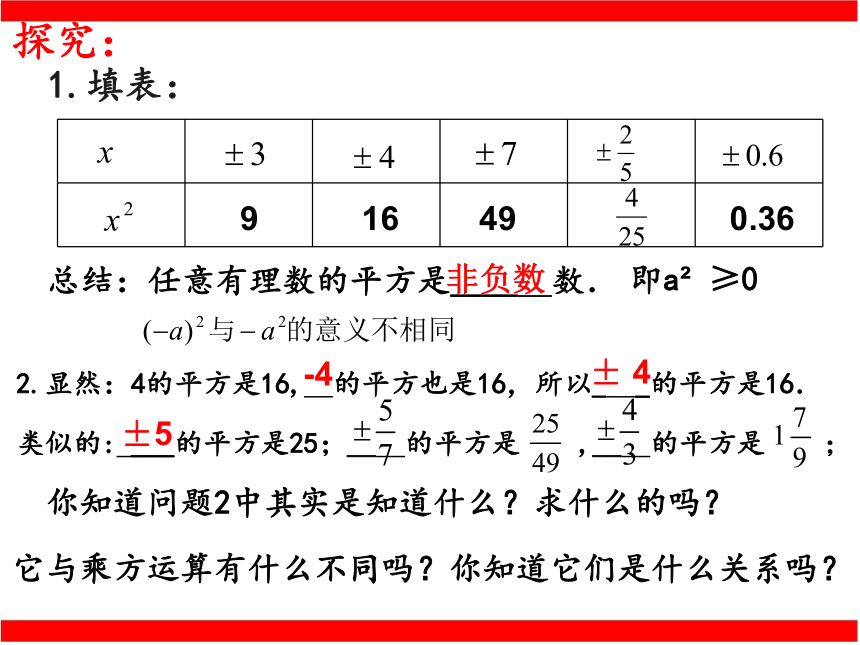
1.填表:
9
16
49
0.36
总结:任意有理数的平方是____ 数.
即a ≥0
你知道问题2中其实是知道什么?求什么的吗?
它与乘方运算有什么不同吗?你知道它们是什么关系吗?
2.显然:4的平方是16, 的平方也是16,所以_ _的平方是16.
类似的: ___的平方是25;__ 的平方是 ,__ 的平方是 ;
探究:
非负数
-4
± 4
±5
例如:
∵ (±1.2)2=1.44
∴ ±1.2叫做1.44的平方根
一般地,如果一个数X的平方等于a,那么这个数X
叫做a的平方根,也叫做a的二次方根。(a≥0)
平方根的概念
符号语言:
∵ x = a
∴ x叫做a的平方根
∵ (±2)2=4 ∴ ±2叫做4的平方根
我们把求一个非负数平方根的运算,叫开平方运算。
它与乘方互为逆运算。
记作:
根指数
被开方数
读作:正负
二次根号a
根号
你知道它们分别是知道什么求什么的吗?
一个非负数a平方根的表示:
±
± =±7
3的平方根是:
±
如:49 的平方根是
则:
其中+ 是a的正的平方根,简记为: ,读作:二次根号a
- 是a的负的平方根,读作:负二次根号a
你能再举出一些数并表示出它们的平方根吗?试试看。
通过举例你有何体会呢?
∵ ( )2 = 0 , ∴ 0的平方根是( )
∵ ( )2等于 -4 , ∴ -4 ( )平方根
∵ (±1.2)2=1.44 ∴ 1.44的平方根是( )
∵ (±2)2=4 ∴ 4的平方根是( )
0
0
不存在
±1.2
±2
没有
得出:
请同学们概括一个数的平方根的性质:
一个正数有两个平方根,它们互为相反数;
零有一个平方根,它是零本身;
负数没有平方根。
平方根的性质:
1.如果 a 的一个平方根是 4,则它的另一个平方根是 .
若a+1平方根是 0,则a= ;
若a+1没有平方根,则a ;
3.判断:下列叙述正确的打“√” ,错误的打“×”:
① 4是16的平方根; ( )
② 16的平方根是4; ( )
③ (-3) 的平方根是3. ( )
④ 1的平方根是1; ( )
⑤ 9的平方根是3; ( )
⑥ 只有一个平方根的数是0;( )
2.若a+1平方根是 ±5 ,则a=_______
小试牛刀:
-4
24
-1
< -1
×
×
×
×
√
√
(1) 9 (2) (3) 0.36 (4)
例1 求下列各数的平方根:
求一个数的平方根的运算叫做开平方。开平方是平方的逆运算。
(1) ∵(±3) =9
(3) ∵(±0.6) =0.36
解:
(2) ∵(± ) =
(4) ∵(± ) =
练习:求下列各数的平方根:
(1)0.25; (2) (3)15 (4)(-2)
例3.求下列各式中的x的值:
(1) x =196 (2)5x -10=0
(3)4(x-3) -9=0
没有
±4
没有
±3
X=±14
X=±
x = 4.5 或 x = 1.5
例2.下列各数有平方根吗?若有,求出它们的平方根;若没有,请说明理由.
(1)-64 (2)(-4) (3) (4)
判断下列说法是否正确:
(1)-9的平方根是-3; ( )
(2)49的平方根是7 ; ( )
(3)(-2)2的平方根是±2 ;( )
(4)1 的平方根是 1 ; ( )
(5)-1 是 1的平方根; ( )
(6)7的平方根是±49. ( )
(7)若X2 = 16 则X = 4 ( )
×
×
√
×
√
×
×
考考你
4 0.01的平方根是 ( )
(A)0.1 (B)±0.1 (C)0.0001 (D)±0.0001
B
C
1.表示121的平方根的数学表达式是( )
A.
B
C.
D.
2.能使x-5有平方根的是( )
A x ≥0 B x >0 C x >5 D x ≥5
3.一个数如果有两个平方根,那么这两个平方根的和是( )
A 大于0 B 等于0 C 小于0 D 大于或等于0
D
D
B
5. ∵ (0.3)2 = 0.09 ∴ ( )
(A)0.09 是 0.3的平方根. (B)0.09是0.3的3倍.
(C)0.3 是0.09 的平方根. (D)0.3不是0.09的平方根.
考考你
选一选
填一填
(1)
(2)
(3)
∵( ) =1
( ) =64
∵ ( ) =0.04
(4)
∵( ) =
即 的平方根是 。
考考你
1、一个数的平方根是-7,则它的另一个平方根
是 , 这个数是 。
2、 的平方根是它本身。
7
49
0
=-0.4
4、 = 。
5、 。
9
6、36的平方根记作( ),值是( )。
3、 。
7、若15是m的一个平方根,则m的另一个平方根是________.
考考你
-15
填一填
9.若5x-1的平方根是±3,4x+2y+1的平方根是
±1,求4x-2y的平方根.
10.求下列各式中的x的值:
(1)x =49 (2)(x-1) =25
(3)4(2x+1) -9=0
8、若某正数x的平方根分别是a+1和a-3,求a的、
值及x的值
考考你
a = 1, x = 4
±4
x=±7
X = 6 或 x = -4
做一做
2.加上开方运算我们已学习了几种基本运算?
①平方根的概念及其表示方法.
课堂小结
加、减、乘、除、乘方、开方六种基本代数运算,这对今后
代数内容学习有着重要的意义。
1.本节主要学习了那些内容?
作业:1.教材P5 练习1.
2.预习学案“自测题”。
②平方根的性质:一个正数有两个平方根,它们互为相反数,
0的平方根是0,负数没有平方根.
③求一个数的平方根的运算—开平方,开方和乘方互为逆运算,
应分清平方运算与开平方运算的区别与联系.
目前为止,我们已学过的表示非负数的式子有那些?
1.若|a+3|=0 则a= ,若
则m= ,若
若|a-3|+
的值为 。
则 a=____
,则代数式
-3
7
5
-1
2.已知:|x+2y|+
求x-3y+4z的值.
拓展提高:
≥0
a≥0, |a|≥0
折纸游戏
如下图,是一个面积为4的正方形纸片.
(1)你能否利用此折出面积为1的小正方形
(2)你能折出面积为2的小正方形吗
(3)折出面积为2的小正方形的边长为多少
课后思考:
6.1 平 方 根
不去耕耘,不去播种,再肥的沃土也长不出庄稼;
不去奋斗,不去创造,再美的青春也结不出硕果。
美国作家杰克伦敦成名后,曾收到过一位女士的求爱信:“你有一个出众的名声,我有一个高贵的地位.这两者加起来,再乘上万能的黄金,足以使我们建立起一个天堂都不能比拟的美满家庭.”
开平方的爱情公式
从这个故事中你发现哪些新的名词?
数学趣事
杰克伦敦连忙回信,他答得很妙:“根据你列出的那道爱情公式,我看还要开平方!不过这个平方根却是负数”.
为了趣味接力比赛,要在运动场上圈出一个面积为100平
方米的正方形场地,这个正方
形场地的边长为多少
10米
身边小事
因为 =100
10
2
?
小明是小学五年级的学生,他非常喜欢画画,这不学校要举行美术作品比赛,小明很高兴,但要求画布面积为50cm 的正方形。可是小明怎么也求不出画布的边长,小明非常着急,只好向上七年级的邻居小娟请教?
身边小事
小娟也犯难了,哪个数的平方是50呢?
小娟想:我还是去学校问老师吧,我一定要认真听讲,
不然不能解决小明的问题,那也太丢面子了。
1.填表:
9
16
49
0.36
总结:任意有理数的平方是____ 数.
即a ≥0
你知道问题2中其实是知道什么?求什么的吗?
它与乘方运算有什么不同吗?你知道它们是什么关系吗?
2.显然:4的平方是16, 的平方也是16,所以_ _的平方是16.
类似的: ___的平方是25;__ 的平方是 ,__ 的平方是 ;
探究:
非负数
-4
± 4
±5
例如:
∵ (±1.2)2=1.44
∴ ±1.2叫做1.44的平方根
一般地,如果一个数X的平方等于a,那么这个数X
叫做a的平方根,也叫做a的二次方根。(a≥0)
平方根的概念
符号语言:
∵ x = a
∴ x叫做a的平方根
∵ (±2)2=4 ∴ ±2叫做4的平方根
我们把求一个非负数平方根的运算,叫开平方运算。
它与乘方互为逆运算。
记作:
根指数
被开方数
读作:正负
二次根号a
根号
你知道它们分别是知道什么求什么的吗?
一个非负数a平方根的表示:
±
± =±7
3的平方根是:
±
如:49 的平方根是
则:
其中+ 是a的正的平方根,简记为: ,读作:二次根号a
- 是a的负的平方根,读作:负二次根号a
你能再举出一些数并表示出它们的平方根吗?试试看。
通过举例你有何体会呢?
∵ ( )2 = 0 , ∴ 0的平方根是( )
∵ ( )2等于 -4 , ∴ -4 ( )平方根
∵ (±1.2)2=1.44 ∴ 1.44的平方根是( )
∵ (±2)2=4 ∴ 4的平方根是( )
0
0
不存在
±1.2
±2
没有
得出:
请同学们概括一个数的平方根的性质:
一个正数有两个平方根,它们互为相反数;
零有一个平方根,它是零本身;
负数没有平方根。
平方根的性质:
1.如果 a 的一个平方根是 4,则它的另一个平方根是 .
若a+1平方根是 0,则a= ;
若a+1没有平方根,则a ;
3.判断:下列叙述正确的打“√” ,错误的打“×”:
① 4是16的平方根; ( )
② 16的平方根是4; ( )
③ (-3) 的平方根是3. ( )
④ 1的平方根是1; ( )
⑤ 9的平方根是3; ( )
⑥ 只有一个平方根的数是0;( )
2.若a+1平方根是 ±5 ,则a=_______
小试牛刀:
-4
24
-1
< -1
×
×
×
×
√
√
(1) 9 (2) (3) 0.36 (4)
例1 求下列各数的平方根:
求一个数的平方根的运算叫做开平方。开平方是平方的逆运算。
(1) ∵(±3) =9
(3) ∵(±0.6) =0.36
解:
(2) ∵(± ) =
(4) ∵(± ) =
练习:求下列各数的平方根:
(1)0.25; (2) (3)15 (4)(-2)
例3.求下列各式中的x的值:
(1) x =196 (2)5x -10=0
(3)4(x-3) -9=0
没有
±4
没有
±3
X=±14
X=±
x = 4.5 或 x = 1.5
例2.下列各数有平方根吗?若有,求出它们的平方根;若没有,请说明理由.
(1)-64 (2)(-4) (3) (4)
判断下列说法是否正确:
(1)-9的平方根是-3; ( )
(2)49的平方根是7 ; ( )
(3)(-2)2的平方根是±2 ;( )
(4)1 的平方根是 1 ; ( )
(5)-1 是 1的平方根; ( )
(6)7的平方根是±49. ( )
(7)若X2 = 16 则X = 4 ( )
×
×
√
×
√
×
×
考考你
4 0.01的平方根是 ( )
(A)0.1 (B)±0.1 (C)0.0001 (D)±0.0001
B
C
1.表示121的平方根的数学表达式是( )
A.
B
C.
D.
2.能使x-5有平方根的是( )
A x ≥0 B x >0 C x >5 D x ≥5
3.一个数如果有两个平方根,那么这两个平方根的和是( )
A 大于0 B 等于0 C 小于0 D 大于或等于0
D
D
B
5. ∵ (0.3)2 = 0.09 ∴ ( )
(A)0.09 是 0.3的平方根. (B)0.09是0.3的3倍.
(C)0.3 是0.09 的平方根. (D)0.3不是0.09的平方根.
考考你
选一选
填一填
(1)
(2)
(3)
∵( ) =1
( ) =64
∵ ( ) =0.04
(4)
∵( ) =
即 的平方根是 。
考考你
1、一个数的平方根是-7,则它的另一个平方根
是 , 这个数是 。
2、 的平方根是它本身。
7
49
0
=-0.4
4、 = 。
5、 。
9
6、36的平方根记作( ),值是( )。
3、 。
7、若15是m的一个平方根,则m的另一个平方根是________.
考考你
-15
填一填
9.若5x-1的平方根是±3,4x+2y+1的平方根是
±1,求4x-2y的平方根.
10.求下列各式中的x的值:
(1)x =49 (2)(x-1) =25
(3)4(2x+1) -9=0
8、若某正数x的平方根分别是a+1和a-3,求a的、
值及x的值
考考你
a = 1, x = 4
±4
x=±7
X = 6 或 x = -4
做一做
2.加上开方运算我们已学习了几种基本运算?
①平方根的概念及其表示方法.
课堂小结
加、减、乘、除、乘方、开方六种基本代数运算,这对今后
代数内容学习有着重要的意义。
1.本节主要学习了那些内容?
作业:1.教材P5 练习1.
2.预习学案“自测题”。
②平方根的性质:一个正数有两个平方根,它们互为相反数,
0的平方根是0,负数没有平方根.
③求一个数的平方根的运算—开平方,开方和乘方互为逆运算,
应分清平方运算与开平方运算的区别与联系.
目前为止,我们已学过的表示非负数的式子有那些?
1.若|a+3|=0 则a= ,若
则m= ,若
若|a-3|+
的值为 。
则 a=____
,则代数式
-3
7
5
-1
2.已知:|x+2y|+
求x-3y+4z的值.
拓展提高:
≥0
a≥0, |a|≥0
折纸游戏
如下图,是一个面积为4的正方形纸片.
(1)你能否利用此折出面积为1的小正方形
(2)你能折出面积为2的小正方形吗
(3)折出面积为2的小正方形的边长为多少
课后思考:
