平行四边形
图片预览

文档简介
平行四边形的性质及判定
名师精讲 1.平行四边形是一种特殊的四边形,它除了具有四边形的性质外,还具有特殊的性质: (1)边:平行四边形两组对边分别平行且相等; (2)角:平行四边形两组对角分别相等,相邻内角互补; (3)对角线:平行四边形对角线互相平分。 (4)推论:夹在两条平行线间的平行线段相等。 平行四边形的定义和性质是今后证明线段相等、两角相等、两直线平行或垂直的重要依据。 2.平行四边形的判定方法:从边上看 从对角线上看:对角线互相平分的四边形是平行四边形。 从角上看:两组对角分别相等的四边形是平行四边形。 注意:平行四边形的定义既是它的一个性质,又可用来判定平行四边形;另外,平行四边形是中心对称图形,两条对角线的交点是它的对称中心。 中考典例 1.(广东省)如图,□ABCD的对角线AC、BD相交于点O,则图中的全等三角形共有 。
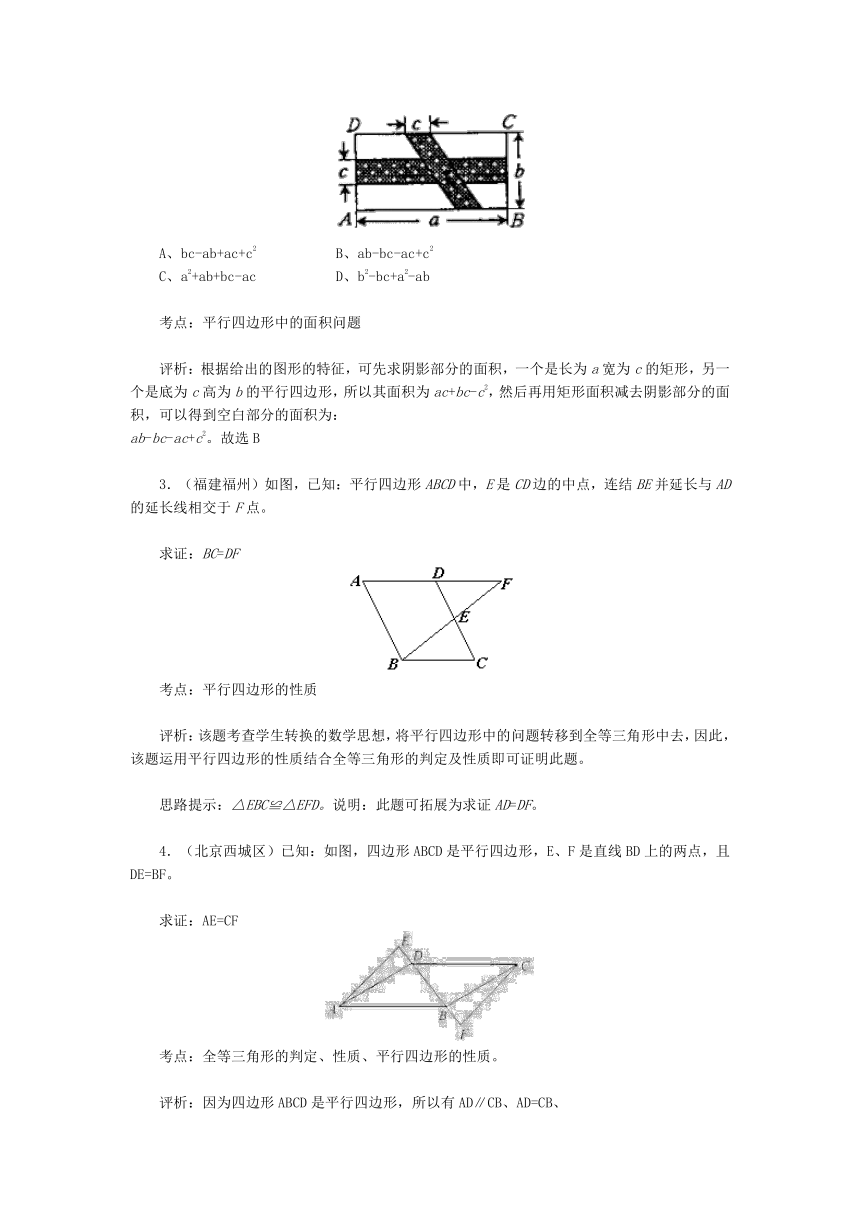
考点:平行四边形的性质 评析:该题考查由平行四边形的性质判定三角形全等,因为平行四边形两组对边分别相等,对角线互相平分,所以图中共有4对全等三角形.分别是△AOB≌△COD,△ABC≌△CDA,△AOD≌△COB,△ABD≌△CDB。 2.(河北省)如图,在矩形ABCD中,横向阴影部分是矩形,另一阴影部分是平行四边形,依照图中标注的数据,计算图中空白部分的面积,其面积是 ( )
A、bc-ab+ac+c2 B、ab-bc-ac+c2 C、a2+ab+bc-ac D、b2-bc+a2-ab 考点:平行四边形中的面积问题 评析:根据给出的图形的特征,可先求阴影部分的面积,一个是长为a宽为c的矩形,另一个是底为c高为b的平行四边形,所以其面积为ac+bc-c2,然后再用矩形面积减去阴影部分的面积,可以得到空白部分的面积为: ab-bc-ac+c2。故选B 3.(福建福州)如图,已知:平行四边形ABCD中,E是CD边的中点,连结BE并延长与AD的延长线相交于F点。 求证:BC=DF
考点:平行四边形的性质 评析:该题考查学生转换的数学思想,将平行四边形中的问题转移到全等三角形中去,因此,该题运用平行四边形的性质结合全等三角形的判定及性质即可证明此题。 思路提示:△EBC≌△EFD。说明:此题可拓展为求证AD=DF。 4.(北京西城区)已知:如图,四边形ABCD是平行四边形,E、F是直线BD上的两点,且DE=BF。 求证:AE=CF
考点:全等三角形的判定、性质、平行四边形的性质。 评析:因为四边形ABCD是平行四边形,所以有AD∥CB、AD=CB、 ∠ADB=∠CBD的结论,又E、D、B、F在同一直线上,所以∠ADE=∠CBF.然后再运用边角边公理证明△ADE≌△CBF,则AE=CF。 说明:一般证线段相等往往证明含两条线段的两个三角形全等.或运用平行四边形的性质.解题过程如下:
证明:∵ 四边形ABCD是平行四边形, ∴ AD∥BC,AD=BC. ∴ ∠1=∠2. ∵ BD是直线, ∴ ∠3=∠4. 在△ADE与△CBF中, ∴ △ADE≌△CBF. ∴ AE=CF. 5.(广东省)如图,在□ABCD中,P1、P2、P3、P4、P5、P6、P7是对角线BD的八等分点.你是否可以从这七个分点中选取两个点,使得以这两点及点A、点C为顶点的四边形是平行四边形?如果可以,请写出一个这样的平行四边形,并给予证明;如果不可以,请说明理由。
考点:平行四边形的判定 评析:运用两组对边分别相等或对角线互相平分的四边形是平行四边形的方法即可判定。因为给的是对角线上的等分点,所以选P1、P7;P2、P6;P3、P5;都可以构成平行四边形。具体解题过程如下: 答:可以,例如四边形AP1CP7就是平行四边形。 证明:∵ 四边形ABCD是平行四边形,
∴ ABDC. ∴ ∠ABP1=∠CDP7. ∵ BP1=DP7=BD, ∴ △ABP1≌△CDP7, ∴ AP1=CP7. 同理可证AP7=CP1. ∴ 四边形AP1CP7是平行四边形
名师精讲 1.平行四边形是一种特殊的四边形,它除了具有四边形的性质外,还具有特殊的性质: (1)边:平行四边形两组对边分别平行且相等; (2)角:平行四边形两组对角分别相等,相邻内角互补; (3)对角线:平行四边形对角线互相平分。 (4)推论:夹在两条平行线间的平行线段相等。 平行四边形的定义和性质是今后证明线段相等、两角相等、两直线平行或垂直的重要依据。 2.平行四边形的判定方法:从边上看 从对角线上看:对角线互相平分的四边形是平行四边形。 从角上看:两组对角分别相等的四边形是平行四边形。 注意:平行四边形的定义既是它的一个性质,又可用来判定平行四边形;另外,平行四边形是中心对称图形,两条对角线的交点是它的对称中心。 中考典例 1.(广东省)如图,□ABCD的对角线AC、BD相交于点O,则图中的全等三角形共有 。
考点:平行四边形的性质 评析:该题考查由平行四边形的性质判定三角形全等,因为平行四边形两组对边分别相等,对角线互相平分,所以图中共有4对全等三角形.分别是△AOB≌△COD,△ABC≌△CDA,△AOD≌△COB,△ABD≌△CDB。 2.(河北省)如图,在矩形ABCD中,横向阴影部分是矩形,另一阴影部分是平行四边形,依照图中标注的数据,计算图中空白部分的面积,其面积是 ( )
A、bc-ab+ac+c2 B、ab-bc-ac+c2 C、a2+ab+bc-ac D、b2-bc+a2-ab 考点:平行四边形中的面积问题 评析:根据给出的图形的特征,可先求阴影部分的面积,一个是长为a宽为c的矩形,另一个是底为c高为b的平行四边形,所以其面积为ac+bc-c2,然后再用矩形面积减去阴影部分的面积,可以得到空白部分的面积为: ab-bc-ac+c2。故选B 3.(福建福州)如图,已知:平行四边形ABCD中,E是CD边的中点,连结BE并延长与AD的延长线相交于F点。 求证:BC=DF
考点:平行四边形的性质 评析:该题考查学生转换的数学思想,将平行四边形中的问题转移到全等三角形中去,因此,该题运用平行四边形的性质结合全等三角形的判定及性质即可证明此题。 思路提示:△EBC≌△EFD。说明:此题可拓展为求证AD=DF。 4.(北京西城区)已知:如图,四边形ABCD是平行四边形,E、F是直线BD上的两点,且DE=BF。 求证:AE=CF
考点:全等三角形的判定、性质、平行四边形的性质。 评析:因为四边形ABCD是平行四边形,所以有AD∥CB、AD=CB、 ∠ADB=∠CBD的结论,又E、D、B、F在同一直线上,所以∠ADE=∠CBF.然后再运用边角边公理证明△ADE≌△CBF,则AE=CF。 说明:一般证线段相等往往证明含两条线段的两个三角形全等.或运用平行四边形的性质.解题过程如下:
证明:∵ 四边形ABCD是平行四边形, ∴ AD∥BC,AD=BC. ∴ ∠1=∠2. ∵ BD是直线, ∴ ∠3=∠4. 在△ADE与△CBF中, ∴ △ADE≌△CBF. ∴ AE=CF. 5.(广东省)如图,在□ABCD中,P1、P2、P3、P4、P5、P6、P7是对角线BD的八等分点.你是否可以从这七个分点中选取两个点,使得以这两点及点A、点C为顶点的四边形是平行四边形?如果可以,请写出一个这样的平行四边形,并给予证明;如果不可以,请说明理由。
考点:平行四边形的判定 评析:运用两组对边分别相等或对角线互相平分的四边形是平行四边形的方法即可判定。因为给的是对角线上的等分点,所以选P1、P7;P2、P6;P3、P5;都可以构成平行四边形。具体解题过程如下: 答:可以,例如四边形AP1CP7就是平行四边形。 证明:∵ 四边形ABCD是平行四边形,
∴ ABDC. ∴ ∠ABP1=∠CDP7. ∵ BP1=DP7=BD, ∴ △ABP1≌△CDP7, ∴ AP1=CP7. 同理可证AP7=CP1. ∴ 四边形AP1CP7是平行四边形
同课章节目录
