北师大版数学七年级下册 第五章生活中的轴对称过关训练 习题课件(共27张PPT)
文档属性
| 名称 | 北师大版数学七年级下册 第五章生活中的轴对称过关训练 习题课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 735.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-24 17:03:21 | ||
图片预览






文档简介
(共27张PPT)
第五章生活中的轴对称过关训练
一、选择题(本大题12小题,每小题3分,共36分)
1.下列轴对称图形中,对称轴最多的是( )
B
2.如图S5-1是小亮在某时从镜子里看到镜子对面
电子钟的像,则这个时刻是( )
A. 10∶21 B. 10∶51 C. 21∶10 D. 12∶01
B
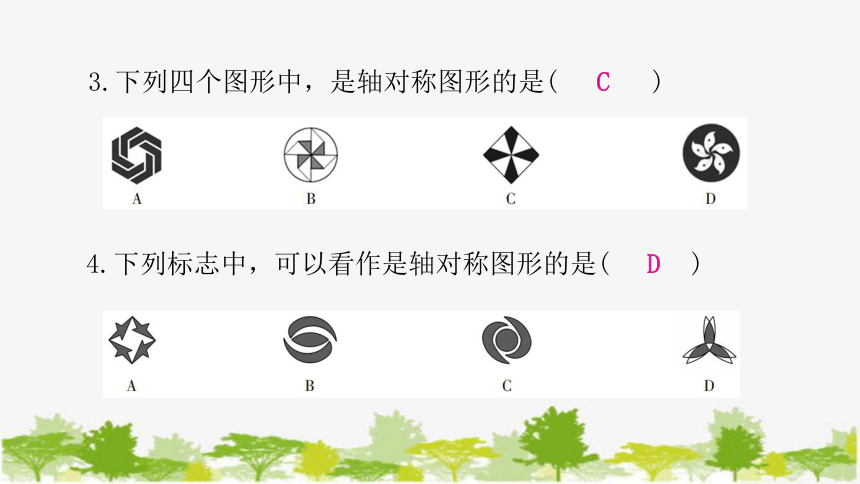
3.下列四个图形中,是轴对称图形的是( )
C
4.下列标志中,可以看作是轴对称图形的是( )
D
5.观察下列作图痕迹,所作线段CD为△ABC的角平分线的是( )
C
6.如图S5-2,已知直线MN 是线段 AB 的垂直平分线,垂足为 N,AM=5 cm,△MAB 的周长为 16 cm,那么 AN等于( )
A. 3 cm B. 4 cm C. 5 cm D. 6 cm
A
7. 下列说法正确的是( )
A. 等腰三角形的高、中线、角平分线互相重合
B. 顶角相等的两个等腰三角形全等
C. 等腰三角形的一边长不可以是另一边长的2倍
D. 等腰三角形的两个底角相等
D
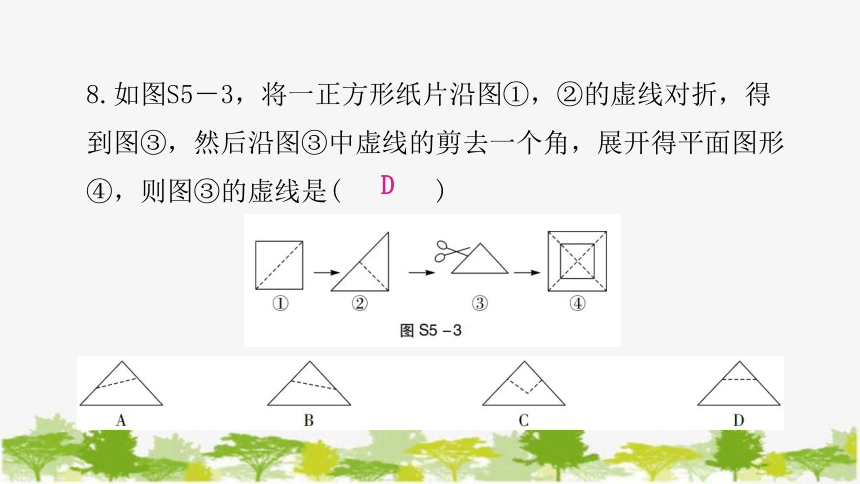
8.如图S5-3,将一正方形纸片沿图①,②的虚线对折,得到图③,然后沿图③中虚线的剪去一个角,展开得平面图形④,则图③的虚线是( )
D
9.剪纸是我国传统的民间艺术.将一张纸片按图S5-4①,②的方式沿虚线依次对折后,再沿图S5-4③中的虚线裁剪,最后将图S5-4④中的纸片打开铺平,所得图案应该是( )
A
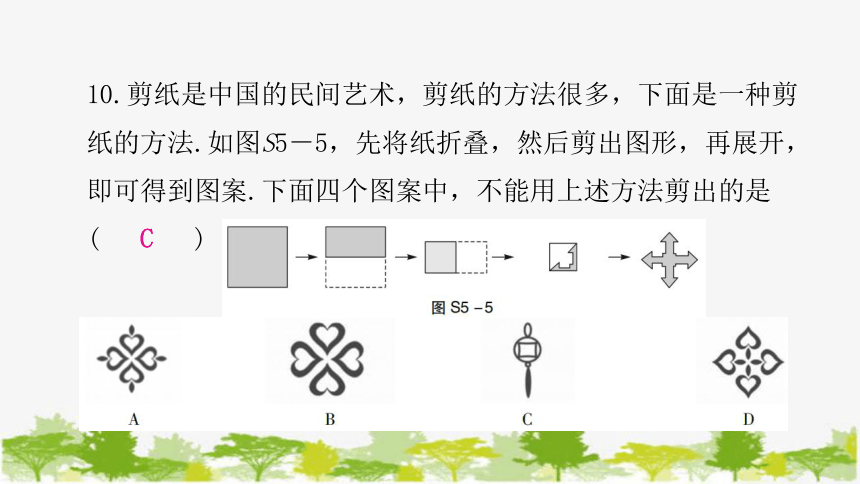
10.剪纸是中国的民间艺术,剪纸的方法很多,下面是一种剪纸的方法.如图S5-5,先将纸折叠,然后剪出图形,再展开,即可得到图案.下面四个图案中,不能用上述方法剪出的是( )
C
11.如图S5-6,在△ABC 中,AD 是 BC 的垂直平分线,若 BC=8,AD=6,则图中阴影部分的面积是( )
A. 48 B. 24 C. 12 D. 6
C
12.如图S5-7,在矩形纸片ABCD中,E,G为AB边上两点,且AE=EG=GB;F,H为CD边上两点,且DF=FH=HC.沿虚线EF折叠,使点A落在点G上,点D落在点H上;然后再沿虚线GH折叠,使B落在点E上,点C落在点F上.叠完后,剪一个直径在EF上的半圆,再展开,则展开后的图形为( )
B
二、填空题(本大题6小题,每小题4分,共24分)
13.一个正五边形的对称轴共有 条.
14.如图S5-8,∠A=30°,∠C′=60°,△ABC与△A′B′C′
关于直线l对称,则∠B= .
5
90°
15.如图S5-9,在△ABC中,∠C=90°,AB=8,BD平分∠ABC.若CD=2,则△ABD的面积为 .
8
16.如图S5-10,在3×3的正方形网格中有两个小正方形被涂灰,再将图中其余小正方形任意一个涂灰,使得整个图形(包括网格)构成一个轴对称图形,那么涂法共有 种.
5
17.如图S5-11,在四边形ABCD中,∠A=100°,∠C=70°,点M,N分别在AB,BC上,将△BMN沿MN翻折后得到△FMN. 若MF∥AD,FN∥DC,则∠B= .
95°
18.如图S5-12,点P为∠AOB内一点,分别作出点P关于OA,OB的对称点P1,P2,连接P1P2交OA于点M,交OB于点N,P1P2=15,则△PMN的周长为 .
15
三、解答题(一)(本大题2小题,每小题8分,共16分)
19.如图S5-13,在方格纸中画出 △ABC 关于直线 MN 对称的 △A1B1C1.
解: 如答图S5-1,△A1B1C1即为所求.
20. 在如图S5-14,等腰三角形ABC中,AB=AC,BC=8,∠BAC=100°,AD是∠BAC的平分线,交BC于点D,AD=4,点E是AB的中点,连接DE.
(1)求∠B的度数;
(2)求△BDE的面积.
解:(1)因为AB=AC,∠BAC=100°,
所以∠B=∠C= (180°-∠BAC)=40°.
(2)因为AB=AC,AD是∠BAC的平分线,
所以AD⊥BC,BD= BC=4.
所以S△ABD= BD·AD= ×4×4=8.
因为点E是AB的中点,所以S△BDE= S△ABD=4.
四、解答题(二)(本大题2小题,每小题10分,共20分)
21.如图S5-15,在 10×10 的方格中有一个四边形和两个三角形(所有顶点都在方格的格点上).
(1)请你画出三个图形关于直线MN 的对称图形;
(2)将(1)中画出的图形与原图形看成一个整体
图形,请写出这个整体图形对称轴的条数.
解:(1) 所画图形如答图S5-2所示.
(2) 这个整体图形共有4 条对称轴.
22.如图S5-16,已知牧马营地在 P 处,每天牧马人要赶着马群先到河边饮水,再带到草地吃草,然后回到营地,请你替牧马人设计出最短的放牧路线.
解:如答图S5-3,作点P
关于河岸的对称点C,作
点P关于草地的对称点 D,
连接 CD,分别与河岸、
草地相交于点 A,B,则最短的放牧路线为 P→A→B→P.
五、解答题(三)(本大题2小题,每小题12分,共24分)
23.如图S5-17,方格纸中每个小正方形的边长均为 1,四边形 ABCD 的四个顶点都在小正方形的顶点上,点 E 在 BC 边上,且点 E 在小正方形的顶点上,连接 AE.
(1)在图中画出△AEF,使 △AEF 与
△AEB 关于直线 AE 对称,点 F 与
点 B 是对称点;
(2)请直接写出△AEF 与四边形 ABCD
重叠部分的面积.
解:(1) 如答图S5-4,△AEF即为所求.
(2)△AEF 与四边形 ABCD 重叠部分的面积为 S=S平行四边形ADCE-S△CEG=2×4- ×2×2=6.
24. 如图S5-18,在△ABC中,AB=AC,D,E是BC边上的点,连接AD,AE,以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,连接D′C,若BD=CD′.
(1)试说明:△ABD≌△ACD′;
(2)若∠BAC=120°,求∠DAE的度数.
解:(1)因为以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,所以AD=AD′.
在△ABD和△ACD′中,
所以△ABD≌△ACD′(SSS).
(2)因为△ABD≌△ACD′,
所以∠BAD=∠CAD′.
所以∠DAC+∠CAD′=∠DAC+∠BAD,即∠DAD′=∠BAC=120°.
因为以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,
所以∠DAE= ∠DAD′=60°.
谢 谢
第五章生活中的轴对称过关训练
一、选择题(本大题12小题,每小题3分,共36分)
1.下列轴对称图形中,对称轴最多的是( )
B
2.如图S5-1是小亮在某时从镜子里看到镜子对面
电子钟的像,则这个时刻是( )
A. 10∶21 B. 10∶51 C. 21∶10 D. 12∶01
B
3.下列四个图形中,是轴对称图形的是( )
C
4.下列标志中,可以看作是轴对称图形的是( )
D
5.观察下列作图痕迹,所作线段CD为△ABC的角平分线的是( )
C
6.如图S5-2,已知直线MN 是线段 AB 的垂直平分线,垂足为 N,AM=5 cm,△MAB 的周长为 16 cm,那么 AN等于( )
A. 3 cm B. 4 cm C. 5 cm D. 6 cm
A
7. 下列说法正确的是( )
A. 等腰三角形的高、中线、角平分线互相重合
B. 顶角相等的两个等腰三角形全等
C. 等腰三角形的一边长不可以是另一边长的2倍
D. 等腰三角形的两个底角相等
D
8.如图S5-3,将一正方形纸片沿图①,②的虚线对折,得到图③,然后沿图③中虚线的剪去一个角,展开得平面图形④,则图③的虚线是( )
D
9.剪纸是我国传统的民间艺术.将一张纸片按图S5-4①,②的方式沿虚线依次对折后,再沿图S5-4③中的虚线裁剪,最后将图S5-4④中的纸片打开铺平,所得图案应该是( )
A
10.剪纸是中国的民间艺术,剪纸的方法很多,下面是一种剪纸的方法.如图S5-5,先将纸折叠,然后剪出图形,再展开,即可得到图案.下面四个图案中,不能用上述方法剪出的是( )
C
11.如图S5-6,在△ABC 中,AD 是 BC 的垂直平分线,若 BC=8,AD=6,则图中阴影部分的面积是( )
A. 48 B. 24 C. 12 D. 6
C
12.如图S5-7,在矩形纸片ABCD中,E,G为AB边上两点,且AE=EG=GB;F,H为CD边上两点,且DF=FH=HC.沿虚线EF折叠,使点A落在点G上,点D落在点H上;然后再沿虚线GH折叠,使B落在点E上,点C落在点F上.叠完后,剪一个直径在EF上的半圆,再展开,则展开后的图形为( )
B
二、填空题(本大题6小题,每小题4分,共24分)
13.一个正五边形的对称轴共有 条.
14.如图S5-8,∠A=30°,∠C′=60°,△ABC与△A′B′C′
关于直线l对称,则∠B= .
5
90°
15.如图S5-9,在△ABC中,∠C=90°,AB=8,BD平分∠ABC.若CD=2,则△ABD的面积为 .
8
16.如图S5-10,在3×3的正方形网格中有两个小正方形被涂灰,再将图中其余小正方形任意一个涂灰,使得整个图形(包括网格)构成一个轴对称图形,那么涂法共有 种.
5
17.如图S5-11,在四边形ABCD中,∠A=100°,∠C=70°,点M,N分别在AB,BC上,将△BMN沿MN翻折后得到△FMN. 若MF∥AD,FN∥DC,则∠B= .
95°
18.如图S5-12,点P为∠AOB内一点,分别作出点P关于OA,OB的对称点P1,P2,连接P1P2交OA于点M,交OB于点N,P1P2=15,则△PMN的周长为 .
15
三、解答题(一)(本大题2小题,每小题8分,共16分)
19.如图S5-13,在方格纸中画出 △ABC 关于直线 MN 对称的 △A1B1C1.
解: 如答图S5-1,△A1B1C1即为所求.
20. 在如图S5-14,等腰三角形ABC中,AB=AC,BC=8,∠BAC=100°,AD是∠BAC的平分线,交BC于点D,AD=4,点E是AB的中点,连接DE.
(1)求∠B的度数;
(2)求△BDE的面积.
解:(1)因为AB=AC,∠BAC=100°,
所以∠B=∠C= (180°-∠BAC)=40°.
(2)因为AB=AC,AD是∠BAC的平分线,
所以AD⊥BC,BD= BC=4.
所以S△ABD= BD·AD= ×4×4=8.
因为点E是AB的中点,所以S△BDE= S△ABD=4.
四、解答题(二)(本大题2小题,每小题10分,共20分)
21.如图S5-15,在 10×10 的方格中有一个四边形和两个三角形(所有顶点都在方格的格点上).
(1)请你画出三个图形关于直线MN 的对称图形;
(2)将(1)中画出的图形与原图形看成一个整体
图形,请写出这个整体图形对称轴的条数.
解:(1) 所画图形如答图S5-2所示.
(2) 这个整体图形共有4 条对称轴.
22.如图S5-16,已知牧马营地在 P 处,每天牧马人要赶着马群先到河边饮水,再带到草地吃草,然后回到营地,请你替牧马人设计出最短的放牧路线.
解:如答图S5-3,作点P
关于河岸的对称点C,作
点P关于草地的对称点 D,
连接 CD,分别与河岸、
草地相交于点 A,B,则最短的放牧路线为 P→A→B→P.
五、解答题(三)(本大题2小题,每小题12分,共24分)
23.如图S5-17,方格纸中每个小正方形的边长均为 1,四边形 ABCD 的四个顶点都在小正方形的顶点上,点 E 在 BC 边上,且点 E 在小正方形的顶点上,连接 AE.
(1)在图中画出△AEF,使 △AEF 与
△AEB 关于直线 AE 对称,点 F 与
点 B 是对称点;
(2)请直接写出△AEF 与四边形 ABCD
重叠部分的面积.
解:(1) 如答图S5-4,△AEF即为所求.
(2)△AEF 与四边形 ABCD 重叠部分的面积为 S=S平行四边形ADCE-S△CEG=2×4- ×2×2=6.
24. 如图S5-18,在△ABC中,AB=AC,D,E是BC边上的点,连接AD,AE,以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,连接D′C,若BD=CD′.
(1)试说明:△ABD≌△ACD′;
(2)若∠BAC=120°,求∠DAE的度数.
解:(1)因为以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,所以AD=AD′.
在△ABD和△ACD′中,
所以△ABD≌△ACD′(SSS).
(2)因为△ABD≌△ACD′,
所以∠BAD=∠CAD′.
所以∠DAC+∠CAD′=∠DAC+∠BAD,即∠DAD′=∠BAC=120°.
因为以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,
所以∠DAE= ∠DAD′=60°.
谢 谢
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
