山东省聊城市2012-2013学年高二上学期“七校联考”期末检测数学文试题
文档属性
| 名称 | 山东省聊城市2012-2013学年高二上学期“七校联考”期末检测数学文试题 |  | |
| 格式 | zip | ||
| 文件大小 | 323.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-07 12:06:02 | ||
图片预览


文档简介
绝密★启用前
山东省聊城市2012-2013学年高二上学期“七校联考”期末检测
文科数学试题
考试时间:100分钟;
题号
一
二
三
总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
评卷人
得分
一、选择题
1.函数f(x)=的零点的个数是( )
A.3个 B.2个 C.1个 D.0个
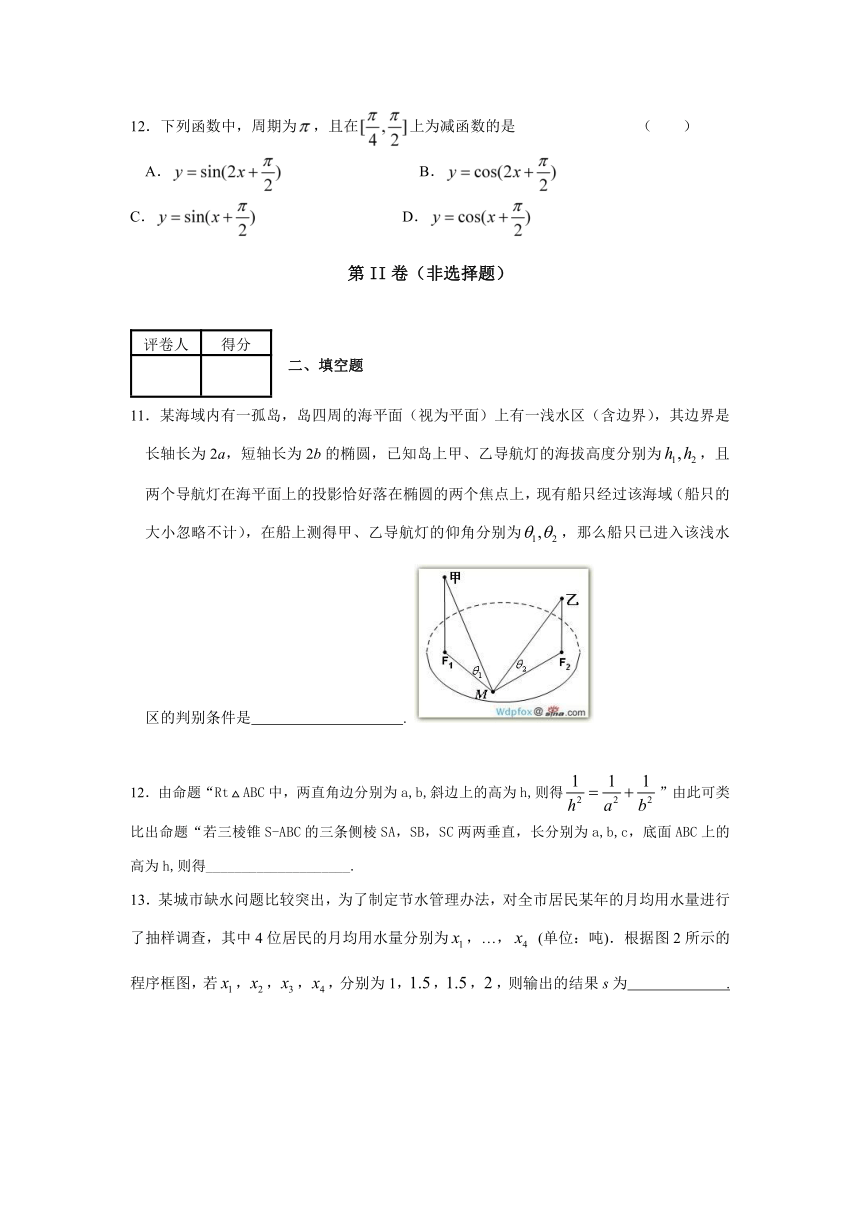
2.(2010年江西理12)如图,一个正五角星薄片(其对称轴与水面垂直)匀速地升出水面,记t时刻五角星露出水面部分的图形面积为,则导函数的图像大致为( )
A.B.C.D.
3.将函数的图象向左平移一个单位,得到图象 ,再将向上平移一个单位得到图象,作出 关于直线 的对称图象 ,则的解析式为( )
A. B.
C. D.
4.已知函数是上的遇函数,若对于,都有,且当时, 的值为 ( )
A.-2 B.-1 C.1 D.2
5.曲线y=x5+3x2+4x在x=-1处的切线的倾斜角是 ( )
A.- B. C. D.
6.·等于( )
A.- B.- C. D.
7.已知集合 ,,
,则的关系 ( )
A. B. C. D.
8.设f(x)=lg(10x+1)+ax是偶函数,g(x)=是奇函数,那么a+b的值为( )
A. 1 B.-1 C.- D.
9.用min{a,b,c}表示a,b,c三个数中的最小值
设f(x)=min{, x+2,10-x} (x 0),则f(x)的最大值为( )
A.4 B.5 C.6 D.7
10.双曲线(,)的左、右焦点分别是,过作倾斜角为的直线交双曲线右支于点,若垂直于轴,则双曲线的离心率为( )
A. B. C. D.
11.已知数列{}的前n项和=-1(a是不为0的常数),那么数列{} ( )
A.一定是等差数列 B.一定是等比数列
C.或者是等差数列或者是等比数列 D.既不是等差数列也不是等比数列
12.下列函数中,周期为,且在上为减函数的是 ( )
A. B.
C. D.
第II卷(非选择题)
评卷人
得分
二、填空题
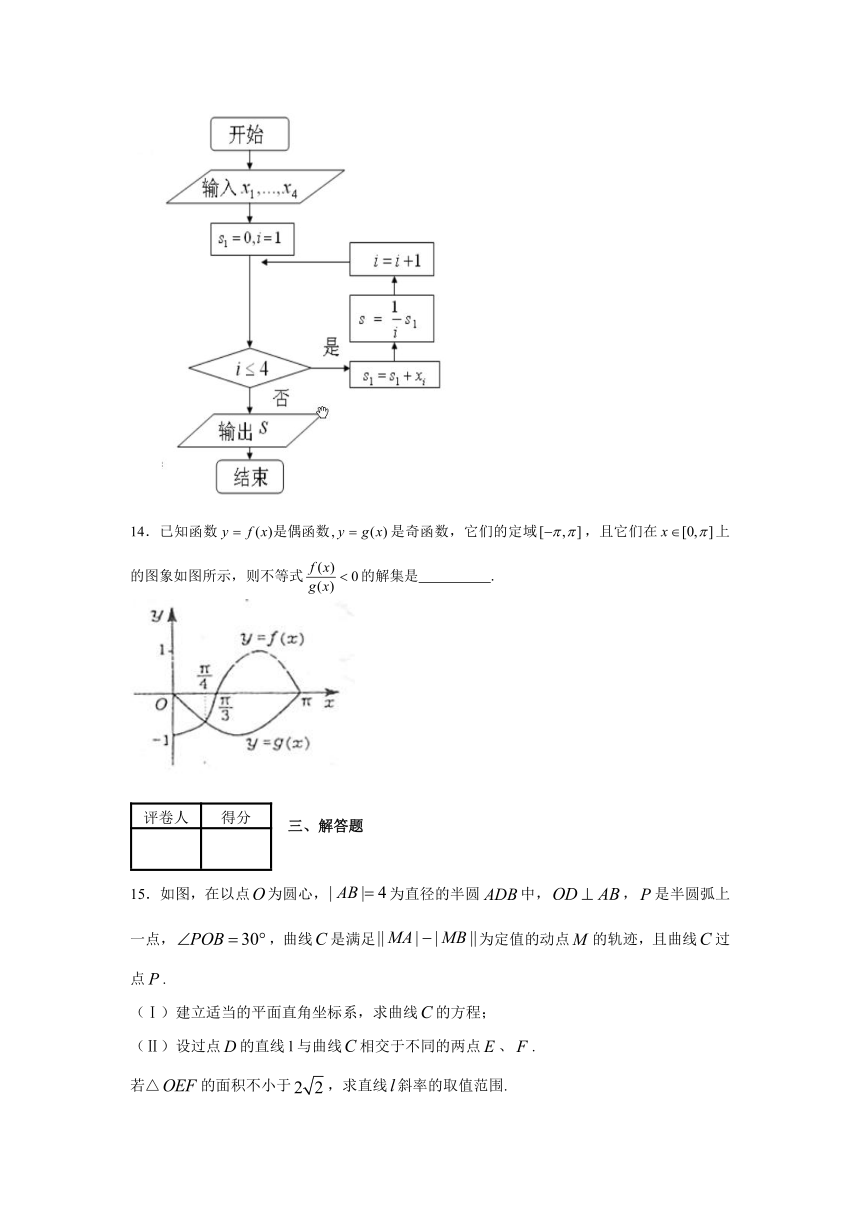
11.某海域内有一孤岛,岛四周的海平面(视为平面)上有一浅水区(含边界),其边界是长轴长为2a,短轴长为2b的椭圆,已知岛上甲、乙导航灯的海拔高度分别为,且两个导航灯在海平面上的投影恰好落在椭圆的两个焦点上,现有船只经过该海域(船只的大小忽略不计),在船上测得甲、乙导航灯的仰角分别为,那么船只已进入该浅水区的判别条件是 .
12.由命题“RtABC中,两直角边分别为a,b,斜边上的高为h,则得”由此可类比出命题“若三棱锥S-ABC的三条侧棱SA,SB,SC两两垂直,长分别为a,b,c,底面ABC上的高为h,则得____________________.
13.某城市缺水问题比较突出,为了制定节水管理办法,对全市居民某年的月均用水量进行了抽样调查,其中4位居民的月均用水量分别为,…, (单位:吨).根据图2所示的程序框图,若,,,,分别为1,,,,则输出的结果s为 .
14.已知函数是奇函数,它们的定域,且它们在上的图象如图所示,则不等式的解集是 .
评卷人
得分
三、解答题
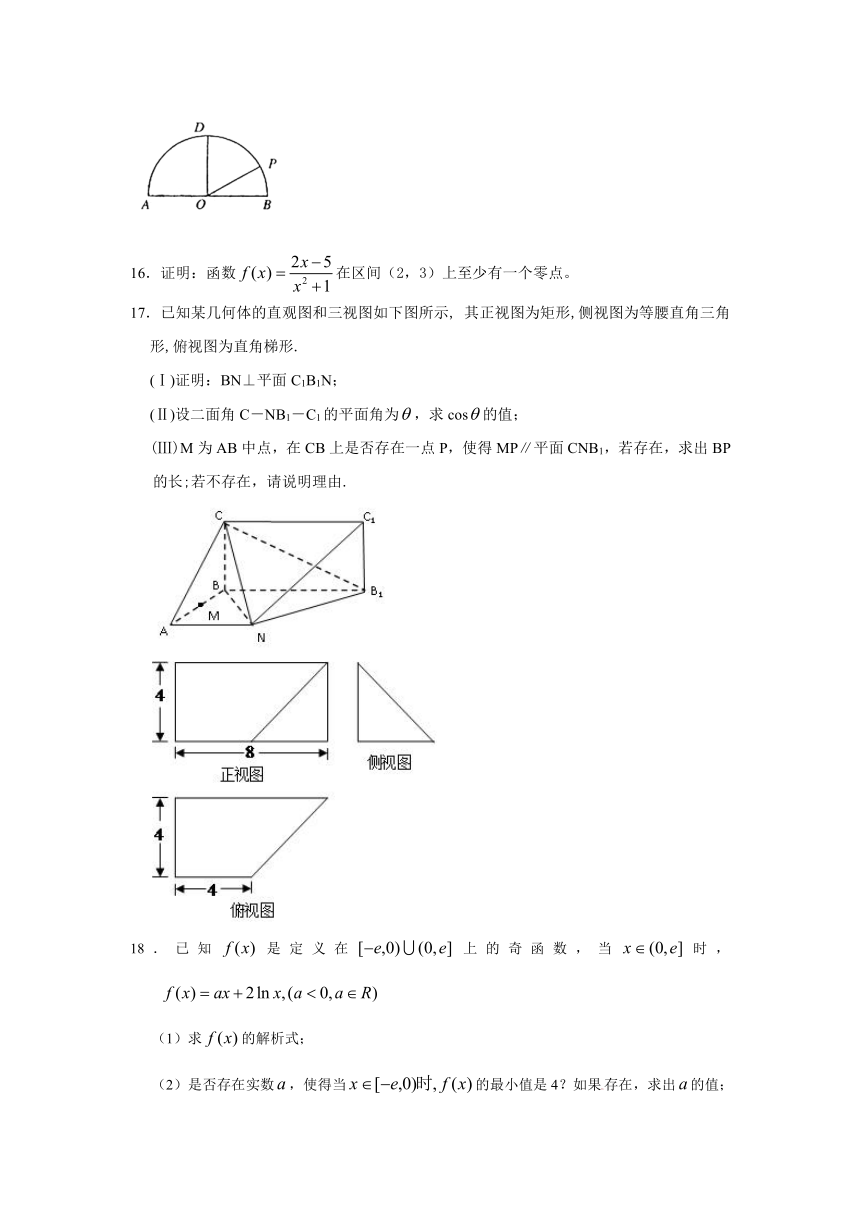
15.如图,在以点为圆心,为直径的半圆中,,是半圆弧上一点,,曲线是满足为定值的动点的轨迹,且曲线过点.
(Ⅰ)建立适当的平面直角坐标系,求曲线的方程;
(Ⅱ)设过点的直线l与曲线相交于不同的两点、.
若△的面积不小于,求直线斜率的取值范围.
16.证明:函数在区间(2,3)上至少有一个零点。
17.已知某几何体的直观图和三视图如下图所示, 其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.
(Ⅰ)证明:BN⊥平面C1B1N;
(Ⅱ)设二面角C-NB1-C1的平面角为,求cos的值;
(Ⅲ)M为AB中点,在CB上是否存在一点P,使得MP∥平面CNB1,若存在,求出BP的长;若不存在,请说明理由.
18.已知是定义在上的奇函数,当时,
(1)求的解析式;
(2)是否存在实数,使得当的最小值是4?如果存在,求出的值;如果不存在,请说明理由。
19.已知函数.
(Ⅰ)若,求曲线在点处的切线方程;
(Ⅱ)若且函数在其定义域内为增函数,求实数的取值范围;
(Ⅲ)若函数在存在极值,求实数的取值范围.
20.设函数f(x)=-ax,(a>0),试确定:当a取什么值时,函数f(x)在0,+∞)上为单调函数.
参考答案
一、选择题
1.B??????
解析:分别画y=lnx和y=的图象;如图。则容易看出,这两个函数有2个交点。即函数f(x)=的零点的个数是2。
2.A??????
解析:本题考查函数图像、导数图、导数的实际意义等知识,重点考查的是对数学的探究能力和应用能力。最初零时刻和最后终点时刻没有变化,导数取零,排除C;总面积一直保持增加,没有负的改变量,排除B;考察A、D的差异在于两肩位置的改变是否平滑,考虑到导数的意义,判断此时面积改变为突变,产生中断,选择A。
3.A??????4.C??????5.C??????6.A??????7.B??????8.D??????9.C??????
解析:画出y=2x ,y=x+2,y=10-x的图象,如右图, 观察图象可知,当0≤x≤2时,f(x)=2x ,当2≤x≤3时,f(x)=x+2,当x>4时,f(x)=10-x,f(x)的最大值在x=4时取得为6,故选C。
10.B??????
解析:如图在中,??? ?? , ?? ?11.C??????
解析:判断该数列是什么数列,可把通项公式求出,再进行判断
12.A??????
二、填空题
13.
14.
15.
16.()
三、解答题
17.(Ⅰ)解法1:以O为原点,AB、OD所在直线分别为x轴、y轴,建立平面直角坐标系,则A(-2,0),B(2,0),D(0,2),P(),依题意得 |MA|-|MB|=|PA|-|PB|= ∴曲线C是以原点为中心,A、B为焦点的双曲线. 设实平轴长为a,虚半轴长为b,半焦距为c, 则c=2,2a=2,∴a2=2,b2=c2-a2=2. ∴曲线C的方程为. 解法2:同解法1建立平面直角坐标系,则依题意可得|MA|-|MB|=|PA|-|PB| |AB|=4. ∴曲线C是以原点为中心,A、B为焦点的双曲线. 设双曲线的方程为>0,b>0). 则由 解得a2=b2=2, ∴曲线C的方程为 (Ⅱ)解法1:依题意,可设直线l的方程为y=kx+2,代入双曲线C的方程并整理得(1-k2)x2-4kx-6=0. ∵直线l与双曲线C相交于不同的两点E、F, ?????????????????????? ② 设E(x,y),F(x2,y2),则由①式得x1+x2=,于是 |EF|= = 而原点O到直线l的距离d=, ∴S△DEF= 若△OEF面积不小于2,即S△OEF,则有 ??????? ③ 综合②、③知,直线l的斜率的取值范围为? 解法2:依题意,可设直线l的方程为y=kx+2,代入双曲线C的方程并整理, 得(1-k2)x2-4kx-6=0. ∵直线l与双曲线C相交于不同的两点E、F, ∴. .????????????????????????????????????? ② 设E(x1,y1),F(x2,y2),则由①式得 |x1-x2|=?????????? ③ 当E、F在同一去上时(如图1所示), S△OEF= 当E、F在不同支上时(如图2所示). S△ODE= 综上得S△OEF=于是 由|OD|=2及③式,得S△OEF= 若△OEF面积不小于2 ???? ④ 综合②、④知,直线l的斜率的取值范围为
18.证明:函数的定义域为R,函数f(x)的图像灾区间(2,3)上是连续的。 又,,f(2)f(3)<0,函数f(x)在区间(2,3)上至少有一个零点。
19.法一:(Ⅰ)证明∵该几何体的正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形, ∴BA,BC,BB1 两两垂直. 以BA,BC,BB1 分别为x,y,z轴建立空间直角坐标系, 则N(4,4,0),B1 (0,8,0),C1 (0,8,4),C(0,0,4) ∵=(4,4,0)·(-4,4,0)=-16+16=0 =(4,4,0)·(0,0,4)=0??? ∴BN⊥NB1 , BN⊥B1 C1 且NB1 与B1 C1 相交于B1 , ∴BN⊥平面C1 B1 N;????????????? (Ⅱ)∵BN⊥平面C1 B1 N, 是平面C1 B1 N的一个法向量=(4,4,0),? 设=(x,y,z)为平面NCB1 的一个法向量, 则,取=(1,1,2),?? 则cosθ===;??? (Ⅲ)∵M(2,0,0).设P(0,0,a)为BC上一点,则=(-2,0,a),∵MP∥平面CNB1 , ∴⊥·=(-2,0,a) ·(1,1,2)=-2+2 a =0 a =1.? 又MP平面CNB1 , ∴MP∥平面CNB1 , ∴当BP=1时MP∥平面CNB1 . 法二:(Ⅰ)证明:由已知得B1 C1 ⊥平面BNB1 ,∴B1 C1 ⊥BN, BN=4= B1 N,BB1 =8, ∴BB1 2 = BN2 + B1 N2 , ∴BN⊥B1 N 又B1 C1 与B1 N交于B1 , ∴BN⊥平面C1 B1 N; (Ⅱ)过N作NQB1 C1 ,则BCQN,又BN⊥平面C1 B1 N, ∴CQ⊥平面C1 B1 N,则CQ⊥B1 N, QN⊥B1 N ,∴∠CNQ是二面角C-B1 N-Q的平面角θ, 在Rt△CNQ中,NQ=4,CQ=4, ∴CN=4,cosθ==; (Ⅲ)延长BA、B1 N交于R,连结CR,∵MP∥平面CNB1 , MP平面CBR, 平面CBR∩平面CRN于CR, ∴MP∥CR, △RB1 B中ANBB1 ,∴A为RB中点, ∴==,∴BP=1,因此存在P点使MP∥平面CNB1 .
20.(1)设????????????? 上的奇函数, ????????????? 故函数的解析式为: ?? (2)假设存在实数,使得当 ????????????? 有最小值是3。 ????????????? ①当时, ????????????? 由于故函数上的增函数。 ????????????? 解得(舍去) ????????????? ②当
x
—
+
↘
↗
????????????? 解得 ????????????? 综上所知,存在实数,使得当最小值4。
21. ????????????? (Ⅱ), ????????????? 要使在定义域内是增函数,只需在内恒成立 ????????????? 即在上恒成立, ????????????? (法一)即在上恒成立 ????????????? ∴,设 ????????????? 则 ????????????? ∵,∴ ,当且仅当时取等号 ????????????? ∴ ,即,∴ ????????????? 所以实数的取值范围是 (法二)令, 要使在定义域内是增函数,只需在内恒成立. 由题意,的图象为开口向上的抛物线, 对称轴方程为,∴, ∴, 解得 ∴实数的取值范围是.(Ⅲ)∵,令,即 设 当时,方程()的解为,此时在无极值, 所以; 当时,的对称轴方程为 ①若在恰好有一个极值 则 ,解得 ????????????? 此时在存在一个极大值;????????????? ????????????? ②若在恰好两个极值,即在有两个不等实根 ????????????? 则 或 ,解得????????????? ????????????? . ????????????? 综上所述,当时,在存在极值.
22.任取x1 、x2 ∈0,+且x1 2 ,则 f(x1 )-f(x2 )=--a(x1 -x2 )=-a(x1 -x2 ) =(x1 -x2 )(-a) (1)当a≥1时,∵ 又∵x1 -x2 1 )-f(x2 )>0,即f(x1 )>f(x2 ) ∴a≥1时,函数f(x)在区间[0,+∞)上为减函数. (2)当01 =0,x2 =,满足f(x1 )=f(x2 )=1 ∴0上不是单调函数 注: ①判断单调性常规思路为定义法; ②变形过程中>|x1 |≥x1 ;>x2 ; ③从a的范围看还须讨论0
山东省聊城市2012-2013学年高二上学期“七校联考”期末检测
文科数学试题
考试时间:100分钟;
题号
一
二
三
总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
评卷人
得分
一、选择题
1.函数f(x)=的零点的个数是( )
A.3个 B.2个 C.1个 D.0个
2.(2010年江西理12)如图,一个正五角星薄片(其对称轴与水面垂直)匀速地升出水面,记t时刻五角星露出水面部分的图形面积为,则导函数的图像大致为( )
A.B.C.D.
3.将函数的图象向左平移一个单位,得到图象 ,再将向上平移一个单位得到图象,作出 关于直线 的对称图象 ,则的解析式为( )
A. B.
C. D.
4.已知函数是上的遇函数,若对于,都有,且当时, 的值为 ( )
A.-2 B.-1 C.1 D.2
5.曲线y=x5+3x2+4x在x=-1处的切线的倾斜角是 ( )
A.- B. C. D.
6.·等于( )
A.- B.- C. D.
7.已知集合 ,,
,则的关系 ( )
A. B. C. D.
8.设f(x)=lg(10x+1)+ax是偶函数,g(x)=是奇函数,那么a+b的值为( )
A. 1 B.-1 C.- D.
9.用min{a,b,c}表示a,b,c三个数中的最小值
设f(x)=min{, x+2,10-x} (x 0),则f(x)的最大值为( )
A.4 B.5 C.6 D.7
10.双曲线(,)的左、右焦点分别是,过作倾斜角为的直线交双曲线右支于点,若垂直于轴,则双曲线的离心率为( )
A. B. C. D.
11.已知数列{}的前n项和=-1(a是不为0的常数),那么数列{} ( )
A.一定是等差数列 B.一定是等比数列
C.或者是等差数列或者是等比数列 D.既不是等差数列也不是等比数列
12.下列函数中,周期为,且在上为减函数的是 ( )
A. B.
C. D.
第II卷(非选择题)
评卷人
得分
二、填空题
11.某海域内有一孤岛,岛四周的海平面(视为平面)上有一浅水区(含边界),其边界是长轴长为2a,短轴长为2b的椭圆,已知岛上甲、乙导航灯的海拔高度分别为,且两个导航灯在海平面上的投影恰好落在椭圆的两个焦点上,现有船只经过该海域(船只的大小忽略不计),在船上测得甲、乙导航灯的仰角分别为,那么船只已进入该浅水区的判别条件是 .
12.由命题“RtABC中,两直角边分别为a,b,斜边上的高为h,则得”由此可类比出命题“若三棱锥S-ABC的三条侧棱SA,SB,SC两两垂直,长分别为a,b,c,底面ABC上的高为h,则得____________________.
13.某城市缺水问题比较突出,为了制定节水管理办法,对全市居民某年的月均用水量进行了抽样调查,其中4位居民的月均用水量分别为,…, (单位:吨).根据图2所示的程序框图,若,,,,分别为1,,,,则输出的结果s为 .
14.已知函数是奇函数,它们的定域,且它们在上的图象如图所示,则不等式的解集是 .
评卷人
得分
三、解答题
15.如图,在以点为圆心,为直径的半圆中,,是半圆弧上一点,,曲线是满足为定值的动点的轨迹,且曲线过点.
(Ⅰ)建立适当的平面直角坐标系,求曲线的方程;
(Ⅱ)设过点的直线l与曲线相交于不同的两点、.
若△的面积不小于,求直线斜率的取值范围.
16.证明:函数在区间(2,3)上至少有一个零点。
17.已知某几何体的直观图和三视图如下图所示, 其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.
(Ⅰ)证明:BN⊥平面C1B1N;
(Ⅱ)设二面角C-NB1-C1的平面角为,求cos的值;
(Ⅲ)M为AB中点,在CB上是否存在一点P,使得MP∥平面CNB1,若存在,求出BP的长;若不存在,请说明理由.
18.已知是定义在上的奇函数,当时,
(1)求的解析式;
(2)是否存在实数,使得当的最小值是4?如果存在,求出的值;如果不存在,请说明理由。
19.已知函数.
(Ⅰ)若,求曲线在点处的切线方程;
(Ⅱ)若且函数在其定义域内为增函数,求实数的取值范围;
(Ⅲ)若函数在存在极值,求实数的取值范围.
20.设函数f(x)=-ax,(a>0),试确定:当a取什么值时,函数f(x)在0,+∞)上为单调函数.
参考答案
一、选择题
1.B??????
解析:分别画y=lnx和y=的图象;如图。则容易看出,这两个函数有2个交点。即函数f(x)=的零点的个数是2。
2.A??????
解析:本题考查函数图像、导数图、导数的实际意义等知识,重点考查的是对数学的探究能力和应用能力。最初零时刻和最后终点时刻没有变化,导数取零,排除C;总面积一直保持增加,没有负的改变量,排除B;考察A、D的差异在于两肩位置的改变是否平滑,考虑到导数的意义,判断此时面积改变为突变,产生中断,选择A。
3.A??????4.C??????5.C??????6.A??????7.B??????8.D??????9.C??????
解析:画出y=2x ,y=x+2,y=10-x的图象,如右图, 观察图象可知,当0≤x≤2时,f(x)=2x ,当2≤x≤3时,f(x)=x+2,当x>4时,f(x)=10-x,f(x)的最大值在x=4时取得为6,故选C。
10.B??????
解析:如图在中,??? ?? , ?? ?11.C??????
解析:判断该数列是什么数列,可把通项公式求出,再进行判断
12.A??????
二、填空题
13.
14.
15.
16.()
三、解答题
17.(Ⅰ)解法1:以O为原点,AB、OD所在直线分别为x轴、y轴,建立平面直角坐标系,则A(-2,0),B(2,0),D(0,2),P(),依题意得 |MA|-|MB|=|PA|-|PB|= ∴曲线C是以原点为中心,A、B为焦点的双曲线. 设实平轴长为a,虚半轴长为b,半焦距为c, 则c=2,2a=2,∴a2=2,b2=c2-a2=2. ∴曲线C的方程为. 解法2:同解法1建立平面直角坐标系,则依题意可得|MA|-|MB|=|PA|-|PB| |AB|=4. ∴曲线C是以原点为中心,A、B为焦点的双曲线. 设双曲线的方程为>0,b>0). 则由 解得a2=b2=2, ∴曲线C的方程为 (Ⅱ)解法1:依题意,可设直线l的方程为y=kx+2,代入双曲线C的方程并整理得(1-k2)x2-4kx-6=0. ∵直线l与双曲线C相交于不同的两点E、F, ?????????????????????? ② 设E(x,y),F(x2,y2),则由①式得x1+x2=,于是 |EF|= = 而原点O到直线l的距离d=, ∴S△DEF= 若△OEF面积不小于2,即S△OEF,则有 ??????? ③ 综合②、③知,直线l的斜率的取值范围为? 解法2:依题意,可设直线l的方程为y=kx+2,代入双曲线C的方程并整理, 得(1-k2)x2-4kx-6=0. ∵直线l与双曲线C相交于不同的两点E、F, ∴. .????????????????????????????????????? ② 设E(x1,y1),F(x2,y2),则由①式得 |x1-x2|=?????????? ③ 当E、F在同一去上时(如图1所示), S△OEF= 当E、F在不同支上时(如图2所示). S△ODE= 综上得S△OEF=于是 由|OD|=2及③式,得S△OEF= 若△OEF面积不小于2 ???? ④ 综合②、④知,直线l的斜率的取值范围为
18.证明:函数的定义域为R,函数f(x)的图像灾区间(2,3)上是连续的。 又,,f(2)f(3)<0,函数f(x)在区间(2,3)上至少有一个零点。
19.法一:(Ⅰ)证明∵该几何体的正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形, ∴BA,BC,BB1 两两垂直. 以BA,BC,BB1 分别为x,y,z轴建立空间直角坐标系, 则N(4,4,0),B1 (0,8,0),C1 (0,8,4),C(0,0,4) ∵=(4,4,0)·(-4,4,0)=-16+16=0 =(4,4,0)·(0,0,4)=0??? ∴BN⊥NB1 , BN⊥B1 C1 且NB1 与B1 C1 相交于B1 , ∴BN⊥平面C1 B1 N;????????????? (Ⅱ)∵BN⊥平面C1 B1 N, 是平面C1 B1 N的一个法向量=(4,4,0),? 设=(x,y,z)为平面NCB1 的一个法向量, 则,取=(1,1,2),?? 则cosθ===;??? (Ⅲ)∵M(2,0,0).设P(0,0,a)为BC上一点,则=(-2,0,a),∵MP∥平面CNB1 , ∴⊥·=(-2,0,a) ·(1,1,2)=-2+2 a =0 a =1.? 又MP平面CNB1 , ∴MP∥平面CNB1 , ∴当BP=1时MP∥平面CNB1 . 法二:(Ⅰ)证明:由已知得B1 C1 ⊥平面BNB1 ,∴B1 C1 ⊥BN, BN=4= B1 N,BB1 =8, ∴BB1 2 = BN2 + B1 N2 , ∴BN⊥B1 N 又B1 C1 与B1 N交于B1 , ∴BN⊥平面C1 B1 N; (Ⅱ)过N作NQB1 C1 ,则BCQN,又BN⊥平面C1 B1 N, ∴CQ⊥平面C1 B1 N,则CQ⊥B1 N, QN⊥B1 N ,∴∠CNQ是二面角C-B1 N-Q的平面角θ, 在Rt△CNQ中,NQ=4,CQ=4, ∴CN=4,cosθ==; (Ⅲ)延长BA、B1 N交于R,连结CR,∵MP∥平面CNB1 , MP平面CBR, 平面CBR∩平面CRN于CR, ∴MP∥CR, △RB1 B中ANBB1 ,∴A为RB中点, ∴==,∴BP=1,因此存在P点使MP∥平面CNB1 .
20.(1)设????????????? 上的奇函数, ????????????? 故函数的解析式为: ?? (2)假设存在实数,使得当 ????????????? 有最小值是3。 ????????????? ①当时, ????????????? 由于故函数上的增函数。 ????????????? 解得(舍去) ????????????? ②当
x
—
+
↘
↗
????????????? 解得 ????????????? 综上所知,存在实数,使得当最小值4。
21. ????????????? (Ⅱ), ????????????? 要使在定义域内是增函数,只需在内恒成立 ????????????? 即在上恒成立, ????????????? (法一)即在上恒成立 ????????????? ∴,设 ????????????? 则 ????????????? ∵,∴ ,当且仅当时取等号 ????????????? ∴ ,即,∴ ????????????? 所以实数的取值范围是 (法二)令, 要使在定义域内是增函数,只需在内恒成立. 由题意,的图象为开口向上的抛物线, 对称轴方程为,∴, ∴, 解得 ∴实数的取值范围是.(Ⅲ)∵,令,即 设 当时,方程()的解为,此时在无极值, 所以; 当时,的对称轴方程为 ①若在恰好有一个极值 则 ,解得 ????????????? 此时在存在一个极大值;????????????? ????????????? ②若在恰好两个极值,即在有两个不等实根 ????????????? 则 或 ,解得????????????? ????????????? . ????????????? 综上所述,当时,在存在极值.
22.任取x1 、x2 ∈0,+且x1 2 ,则 f(x1 )-f(x2 )=--a(x1 -x2 )=-a(x1 -x2 ) =(x1 -x2 )(-a) (1)当a≥1时,∵ 又∵x1 -x2 1 )-f(x2 )>0,即f(x1 )>f(x2 ) ∴a≥1时,函数f(x)在区间[0,+∞)上为减函数. (2)当01 =0,x2 =,满足f(x1 )=f(x2 )=1 ∴0上不是单调函数 注: ①判断单调性常规思路为定义法; ②变形过程中>|x1 |≥x1 ;>x2 ; ③从a的范围看还须讨论0
同课章节目录
