山东省聊城市2012-2013学年高二上学期“七校联考”期末检测数学理试题
文档属性
| 名称 | 山东省聊城市2012-2013学年高二上学期“七校联考”期末检测数学理试题 | 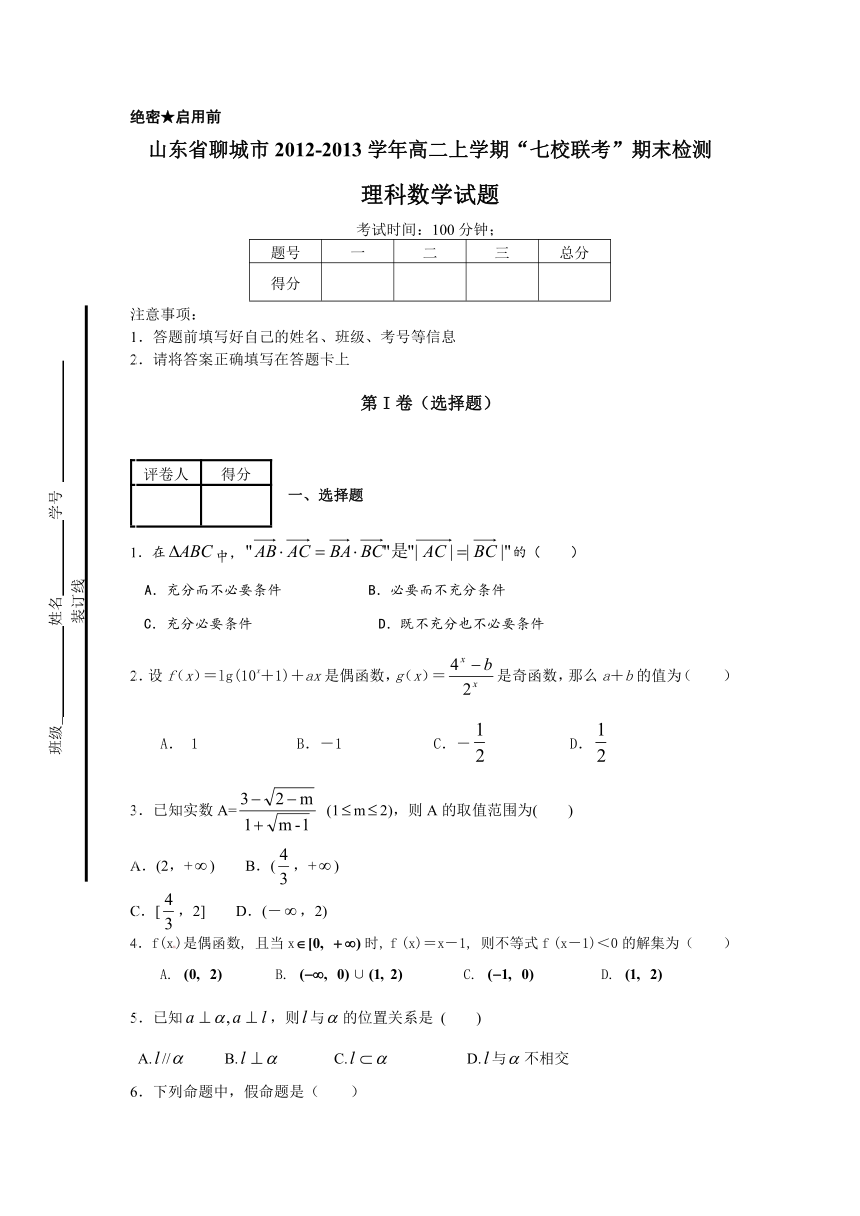 | |
| 格式 | zip | ||
| 文件大小 | 180.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-07 12:06:28 | ||
图片预览




文档简介
绝密★启用前
山东省聊城市2012-2013学年高二上学期“七校联考”期末检测
理科数学试题
考试时间:100分钟;
题号
一
二
三
总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
评卷人
得分
一、选择题
1.在中,的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
2.设f(x)=lg(10x+1)+ax是偶函数,g(x)=是奇函数,那么a+b的值为( )
A. 1 B.-1 C.- D.
3.已知实数A= (1m2),则A的取值范围为( )
A.(2,+) B.(,+)
C.[,2] D.(-,2)
4.f(x)是偶函数, 且当x时, f (x)=x-1, 则不等式f (x-1)<0的解集为( )
A. B. ∪ C. D.
5.已知,则与的位置关系是 ( )
A.// B. C. D.与不相交
6.下列命题中,假命题是( )
A.以矩形的一边所在的直线为旋转轴,其余三边旋转形成的曲面所围成的几何体叫圆柱
B.以直角三角形的一边所在直线为旋转轴,其余两边旋转形成的曲面围成的几何体叫圆锥
C.以直角三角形一条直角边所在直线为旋转轴,其余两边旋转形成的曲面围成的几何体叫圆锥
D.以等腰三角形的底边上的高所在直线为旋转轴,其余各边旋转形成曲面围成的几何体叫圆锥
7.正四面体的4个面上分别写着1、2、3、4,将3个这样均匀的正四面体同时投掷于桌面上,与桌面接触的3个面上的3个数的乘积能被4整除的概率是 ( )
A. B. C. D.
8.拟定从甲地到乙地通话m分钟的电话费由f(m)=1.06×(0.5·[m]+1)(元)决定,其中m>0,[m]是大于或等于m的最小整数,则从甲地到乙地通话时间为5.5分钟的电话费为( )
A.3.71元 B.3.97元 C.4.24元 D.4.77元
9.如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点,将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则三棱锥P-DCE的外接球的体积为( )
A. B. C. D.
10.设,集合,则( )
A.1 B. C.2 D.
11.设S是至少含有两个元素的集合,在S上定义了一个二元运算“*”(即对任意的,对于有序元素对,在S中有唯一确定的元素与之对应)。若对于任意的,有,则对任意的,下列等式中不恒成立的是( )
A. B.
C. D.
12.下列函数中,周期为,且在上为减函数的是 ( )
A. B.
C. D.
第II卷(非选择题)
评卷人
得分
二、填空题
13.已知,则
14.设F为抛物线的焦点,A、B为该抛物线上的两点,若,则 。
15.设P是一个数集,且至少含有两个数,若对任意,都有(除数),则称P是一个数域.例如有理数集Q是数域;数集也是数域.有下列命题:
①整数集是数域; ②若有理数集,则数集M必为数域;
③数域必为无限集; ④存在无穷多个数域.
其中正确的命题的序号是 .(把你认为正确的命题的序号填填上)
16.函数对一切实数都满足,并且方程有三个实根,则这三个实根的和为
评卷人
得分
三、解答题
17.如图,直角梯形ABCD中,∠,AD∥BC,AB=2,AD=,BC=
椭圆F以A、B为焦点,且经过点D,
(Ⅰ)建立适当的直角坐标系,求椭圆F的方程;
(Ⅱ)是否存在直线与两点,且线段,若存在,求直线的方程;若不存在,说明理由。
18.
已知集合对于,,定义A与B的差为 与之间的距离为
(Ⅰ)当n=5时,设,求,;
(Ⅱ)证明:,且;
(Ⅲ) 证明:三个数中至少有一个是偶数
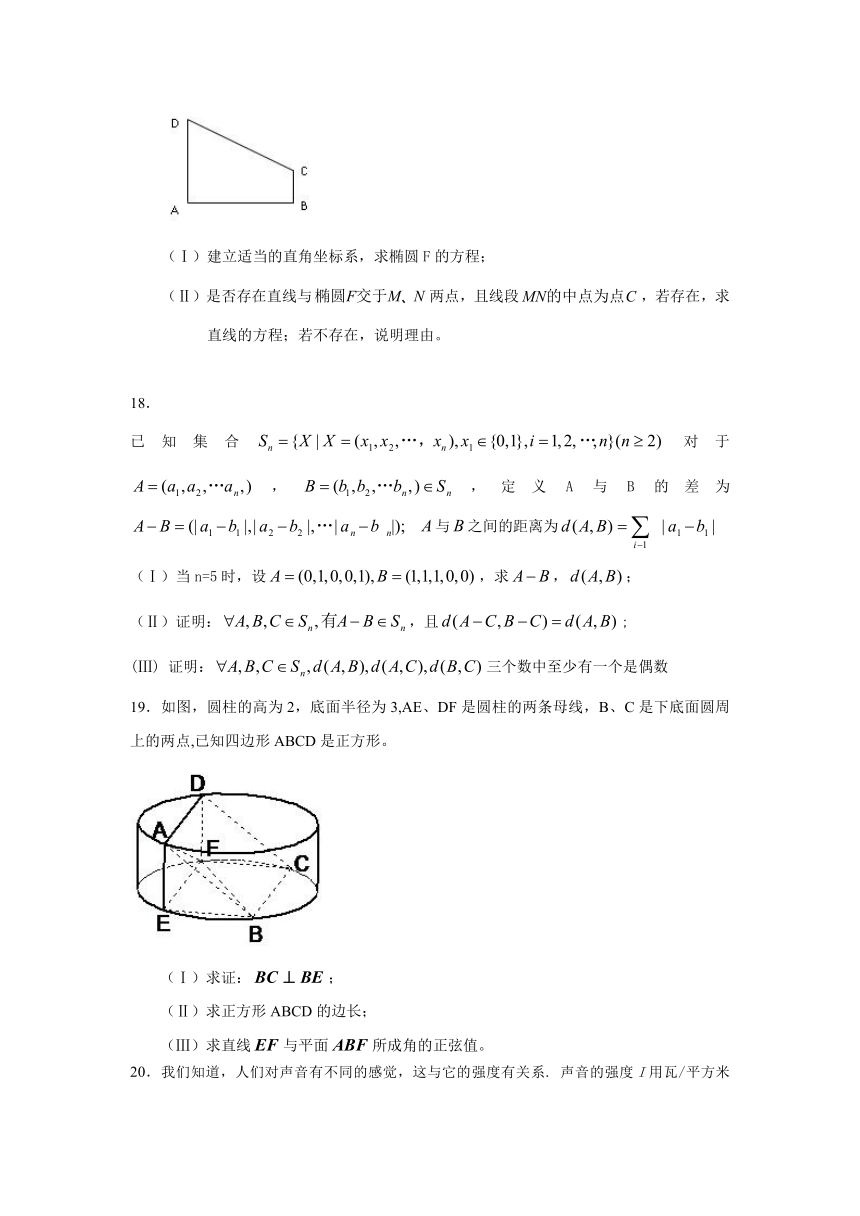
19.如图,圆柱的高为2,底面半径为3,AE、DF是圆柱的两条母线,B、C是下底面圆周上的两点,已知四边形ABCD是正方形。
(Ⅰ)求证:;
(Ⅱ)求正方形ABCD的边长;
(Ⅲ)求直线与平面所成角的正弦值。
20.我们知道,人们对声音有不同的感觉,这与它的强度有关系. 声音的强度I用瓦/平方米 ()表示。但在实际测量中,常用声音的强度水平表示,它们满足以下公式: (单位为分贝),,其中,这是人们平均能听到的最小强度,是听觉的开端。回答以下问题:
(1)树叶沙沙声的强度是,耳语的强度是,恬静的无限电广播的强度为, 试分别求出它们的强度水平。(2)在某一新建的安静小区规定:小区内的公共场所声音的强度水平必须保持在50分贝以下,试求声音强度I的范围为多少?
21.某工厂生产一种仪器的元件,由于受生产能力和技术水平的限制,会产生一些次品,根据经验知道,其次品率与日产量(万件)之间大体满足关系:
(其中为小于6的正常数)
(注:次品率=次品数/生产量,如表示每生产10件产品,有1件为次品,其余为合格品)已知每生产1万件合格的仪器可以盈利2万元,但每生产1万件次品将亏损1万元,故厂方希望定出合适的日产量.
(1)试将生产这种仪器的元件每天的盈利额(万元)表示为日产量(万件)的函数;
(2)当日产量为多少时,可获得最大利润?
22.某种空气清洁剂在实验效果时,发现空气含剂量与时间之间存在函数关系,其变化的图像如下图所示。其中的曲线部分是某函数的图像(虚线部分为曲线的延展).图中表明,喷洒1小时后,空气含剂量最高,达到,以后逐步减小。
(1)求出空气含剂量关于时间的函数表达式及定义域.
(2)实验证明,当空气含剂量不低于时,空气清洁的效果最佳。求一次喷洒的“最佳效果”持续时间.
参考答案
一、选择题
1.C??????2.D??????3.C??????
解析:观察表达式的结构特征.可表示为两点的斜率,所以构造动点P(x.y),则,所以x2 +y2 =1.一1x0,0y1,所求即为过点M(1,3)的直线系与四分之一单位圆有交点的斜率的取值范围,画出草图(图略),注意特殊点B(0,1).kMB =2.利用直线y-3=k(x-1)和圆x2 +y2 =1,-1x0,0y1相切的条件,有,数形结合,得A的取值范围为[.2]
4.A??????5.D??????6.B??????7.B??????8.C??????9.C??????10.C??????11.A??????
12.A
二、填空题
13.-26
14.6
15.③④
16.
三、解答题
17.(Ⅰ)(Ⅰ)以AB中点为原点O,AB所在直线为x轴,建立直角坐标系,如图 ?????? 则A(-1,0)?? B(1,0)???? D(-1,)??????? ????? 设椭圆F的方程为?? ???? 得?????????????????? ?????????????????????????????? ???? 得 ???? 所求椭圆F方程
18.(Ⅰ)解:=(1,0,1,0,1) ???????? =3 (Ⅱ)证明:设 ???????? 因为,所以 从而 由题意知 当时, 当时, 所以 (Ⅲ)证明:设 记由(Ⅱ)可知 所以中1的个数为k,中1的个数为 设是使成立的的个数。则 由此可知,三个数不可能都是奇数 即三个数中至少有一个是偶数。
19.解:(1) AE是圆柱的母线底面BEFC, 又面BEFC?? ???? 又ABCD是正方形 又面ABE???? 又面ABE? ?? (2)四边形为矩形,且ABCD是正方形 EFBC?????????? 四边形EFBC为矩形? BF为圆柱下底面的直径????? 设正方形ABCD的边长为,则AD=EF=AB= 在直角中AE=2,AB=,且BE2 +AE2 = AB2 ,得BE2 =2 -4???????? 在直角中BF=6,EF=,且BE2 +EF2 = BF2 ,的BE2 =36-2??? 解得=,即正方形ABCD的边长为????? (3)解法一:如图以F为原点建立空间直角坐标系, 则A(,0,2),B(,4,0)????????????? ,E(,0,0), (,0, 2),(,4,0), (,0,0) 设面AEF的法向量为(,,),则 ? 令,则即(????????????? ,,) 设直线与平面所成角的大小为,则 所以直线与平面所成角的正弦值为。?? 如图以E为原点建立空间直角坐标系, 则A(0,0,2)????????????? ,B(4,0,0)????????????? ,F(0,,0)????????????? , (-4,,0), (0,,-2)????????????? , (0,,0)? 设面AEF的法向量为(,,)????????????? ,则 ??? 令,则即(????????????? ,,) 设直线与平面所成角的大小为,则 ? 所以直线与平面所成角的正弦值为。
20.解:(1)树叶沙沙声的强度水平:(分贝); 耳语的强度水平:(分贝); 恬静的无限电广播的强度水平:(分贝). (2)由,即,
21.解:(1)当时,,[来源 当时,, 综上,日盈利额(万元)与日产量(万件)的函数关系为: (2)由(1)知,当时,每天的盈利额为0 ??????? 当时, 当且仅当时取等号 所以当时,,此时 ??????????? 当时,由知 函数在上递增,,此时 综上,若,则当日产量为3万件时,可获得最大利润 ??????? 若,则当日产量为万件时,可获得最大利润
22.(1)当时,图像是一线段,得解析式为,将点坐标代入得,∴ 对于函数将点坐标代入得. ∴,令得 ∴函数的解析式为: (2)当时,在中令得 当时,在中,令得: ,从而 ,故最佳效果持续时间为小时.
山东省聊城市2012-2013学年高二上学期“七校联考”期末检测
理科数学试题
考试时间:100分钟;
题号
一
二
三
总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
评卷人
得分
一、选择题
1.在中,的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
2.设f(x)=lg(10x+1)+ax是偶函数,g(x)=是奇函数,那么a+b的值为( )
A. 1 B.-1 C.- D.
3.已知实数A= (1m2),则A的取值范围为( )
A.(2,+) B.(,+)
C.[,2] D.(-,2)
4.f(x)是偶函数, 且当x时, f (x)=x-1, 则不等式f (x-1)<0的解集为( )
A. B. ∪ C. D.
5.已知,则与的位置关系是 ( )
A.// B. C. D.与不相交
6.下列命题中,假命题是( )
A.以矩形的一边所在的直线为旋转轴,其余三边旋转形成的曲面所围成的几何体叫圆柱
B.以直角三角形的一边所在直线为旋转轴,其余两边旋转形成的曲面围成的几何体叫圆锥
C.以直角三角形一条直角边所在直线为旋转轴,其余两边旋转形成的曲面围成的几何体叫圆锥
D.以等腰三角形的底边上的高所在直线为旋转轴,其余各边旋转形成曲面围成的几何体叫圆锥
7.正四面体的4个面上分别写着1、2、3、4,将3个这样均匀的正四面体同时投掷于桌面上,与桌面接触的3个面上的3个数的乘积能被4整除的概率是 ( )
A. B. C. D.
8.拟定从甲地到乙地通话m分钟的电话费由f(m)=1.06×(0.5·[m]+1)(元)决定,其中m>0,[m]是大于或等于m的最小整数,则从甲地到乙地通话时间为5.5分钟的电话费为( )
A.3.71元 B.3.97元 C.4.24元 D.4.77元
9.如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点,将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则三棱锥P-DCE的外接球的体积为( )
A. B. C. D.
10.设,集合,则( )
A.1 B. C.2 D.
11.设S是至少含有两个元素的集合,在S上定义了一个二元运算“*”(即对任意的,对于有序元素对,在S中有唯一确定的元素与之对应)。若对于任意的,有,则对任意的,下列等式中不恒成立的是( )
A. B.
C. D.
12.下列函数中,周期为,且在上为减函数的是 ( )
A. B.
C. D.
第II卷(非选择题)
评卷人
得分
二、填空题
13.已知,则
14.设F为抛物线的焦点,A、B为该抛物线上的两点,若,则 。
15.设P是一个数集,且至少含有两个数,若对任意,都有(除数),则称P是一个数域.例如有理数集Q是数域;数集也是数域.有下列命题:
①整数集是数域; ②若有理数集,则数集M必为数域;
③数域必为无限集; ④存在无穷多个数域.
其中正确的命题的序号是 .(把你认为正确的命题的序号填填上)
16.函数对一切实数都满足,并且方程有三个实根,则这三个实根的和为
评卷人
得分
三、解答题
17.如图,直角梯形ABCD中,∠,AD∥BC,AB=2,AD=,BC=
椭圆F以A、B为焦点,且经过点D,
(Ⅰ)建立适当的直角坐标系,求椭圆F的方程;
(Ⅱ)是否存在直线与两点,且线段,若存在,求直线的方程;若不存在,说明理由。
18.
已知集合对于,,定义A与B的差为 与之间的距离为
(Ⅰ)当n=5时,设,求,;
(Ⅱ)证明:,且;
(Ⅲ) 证明:三个数中至少有一个是偶数
19.如图,圆柱的高为2,底面半径为3,AE、DF是圆柱的两条母线,B、C是下底面圆周上的两点,已知四边形ABCD是正方形。
(Ⅰ)求证:;
(Ⅱ)求正方形ABCD的边长;
(Ⅲ)求直线与平面所成角的正弦值。
20.我们知道,人们对声音有不同的感觉,这与它的强度有关系. 声音的强度I用瓦/平方米 ()表示。但在实际测量中,常用声音的强度水平表示,它们满足以下公式: (单位为分贝),,其中,这是人们平均能听到的最小强度,是听觉的开端。回答以下问题:
(1)树叶沙沙声的强度是,耳语的强度是,恬静的无限电广播的强度为, 试分别求出它们的强度水平。(2)在某一新建的安静小区规定:小区内的公共场所声音的强度水平必须保持在50分贝以下,试求声音强度I的范围为多少?
21.某工厂生产一种仪器的元件,由于受生产能力和技术水平的限制,会产生一些次品,根据经验知道,其次品率与日产量(万件)之间大体满足关系:
(其中为小于6的正常数)
(注:次品率=次品数/生产量,如表示每生产10件产品,有1件为次品,其余为合格品)已知每生产1万件合格的仪器可以盈利2万元,但每生产1万件次品将亏损1万元,故厂方希望定出合适的日产量.
(1)试将生产这种仪器的元件每天的盈利额(万元)表示为日产量(万件)的函数;
(2)当日产量为多少时,可获得最大利润?
22.某种空气清洁剂在实验效果时,发现空气含剂量与时间之间存在函数关系,其变化的图像如下图所示。其中的曲线部分是某函数的图像(虚线部分为曲线的延展).图中表明,喷洒1小时后,空气含剂量最高,达到,以后逐步减小。
(1)求出空气含剂量关于时间的函数表达式及定义域.
(2)实验证明,当空气含剂量不低于时,空气清洁的效果最佳。求一次喷洒的“最佳效果”持续时间.
参考答案
一、选择题
1.C??????2.D??????3.C??????
解析:观察表达式的结构特征.可表示为两点的斜率,所以构造动点P(x.y),则,所以x2 +y2 =1.一1x0,0y1,所求即为过点M(1,3)的直线系与四分之一单位圆有交点的斜率的取值范围,画出草图(图略),注意特殊点B(0,1).kMB =2.利用直线y-3=k(x-1)和圆x2 +y2 =1,-1x0,0y1相切的条件,有,数形结合,得A的取值范围为[.2]
4.A??????5.D??????6.B??????7.B??????8.C??????9.C??????10.C??????11.A??????
12.A
二、填空题
13.-26
14.6
15.③④
16.
三、解答题
17.(Ⅰ)(Ⅰ)以AB中点为原点O,AB所在直线为x轴,建立直角坐标系,如图 ?????? 则A(-1,0)?? B(1,0)???? D(-1,)??????? ????? 设椭圆F的方程为?? ???? 得?????????????????? ?????????????????????????????? ???? 得 ???? 所求椭圆F方程
18.(Ⅰ)解:=(1,0,1,0,1) ???????? =3 (Ⅱ)证明:设 ???????? 因为,所以 从而 由题意知 当时, 当时, 所以 (Ⅲ)证明:设 记由(Ⅱ)可知 所以中1的个数为k,中1的个数为 设是使成立的的个数。则 由此可知,三个数不可能都是奇数 即三个数中至少有一个是偶数。
19.解:(1) AE是圆柱的母线底面BEFC, 又面BEFC?? ???? 又ABCD是正方形 又面ABE???? 又面ABE? ?? (2)四边形为矩形,且ABCD是正方形 EFBC?????????? 四边形EFBC为矩形? BF为圆柱下底面的直径????? 设正方形ABCD的边长为,则AD=EF=AB= 在直角中AE=2,AB=,且BE2 +AE2 = AB2 ,得BE2 =2 -4???????? 在直角中BF=6,EF=,且BE2 +EF2 = BF2 ,的BE2 =36-2??? 解得=,即正方形ABCD的边长为????? (3)解法一:如图以F为原点建立空间直角坐标系, 则A(,0,2),B(,4,0)????????????? ,E(,0,0), (,0, 2),(,4,0), (,0,0) 设面AEF的法向量为(,,),则 ? 令,则即(????????????? ,,) 设直线与平面所成角的大小为,则 所以直线与平面所成角的正弦值为。?? 如图以E为原点建立空间直角坐标系, 则A(0,0,2)????????????? ,B(4,0,0)????????????? ,F(0,,0)????????????? , (-4,,0), (0,,-2)????????????? , (0,,0)? 设面AEF的法向量为(,,)????????????? ,则 ??? 令,则即(????????????? ,,) 设直线与平面所成角的大小为,则 ? 所以直线与平面所成角的正弦值为。
20.解:(1)树叶沙沙声的强度水平:(分贝); 耳语的强度水平:(分贝); 恬静的无限电广播的强度水平:(分贝). (2)由,即,
21.解:(1)当时,,[来源 当时,, 综上,日盈利额(万元)与日产量(万件)的函数关系为: (2)由(1)知,当时,每天的盈利额为0 ??????? 当时, 当且仅当时取等号 所以当时,,此时 ??????????? 当时,由知 函数在上递增,,此时 综上,若,则当日产量为3万件时,可获得最大利润 ??????? 若,则当日产量为万件时,可获得最大利润
22.(1)当时,图像是一线段,得解析式为,将点坐标代入得,∴ 对于函数将点坐标代入得. ∴,令得 ∴函数的解析式为: (2)当时,在中令得 当时,在中,令得: ,从而 ,故最佳效果持续时间为小时.
同课章节目录
