华师大版数学八下 19.1.1矩形的性质课件(共18张PPT)
文档属性
| 名称 | 华师大版数学八下 19.1.1矩形的性质课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 725.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-24 17:36:55 | ||
图片预览

文档简介
(共18张PPT)
19.1 矩 形
1 矩形的性质
第19章 矩形、菱形与正方形
华东师大·八年级数学下册
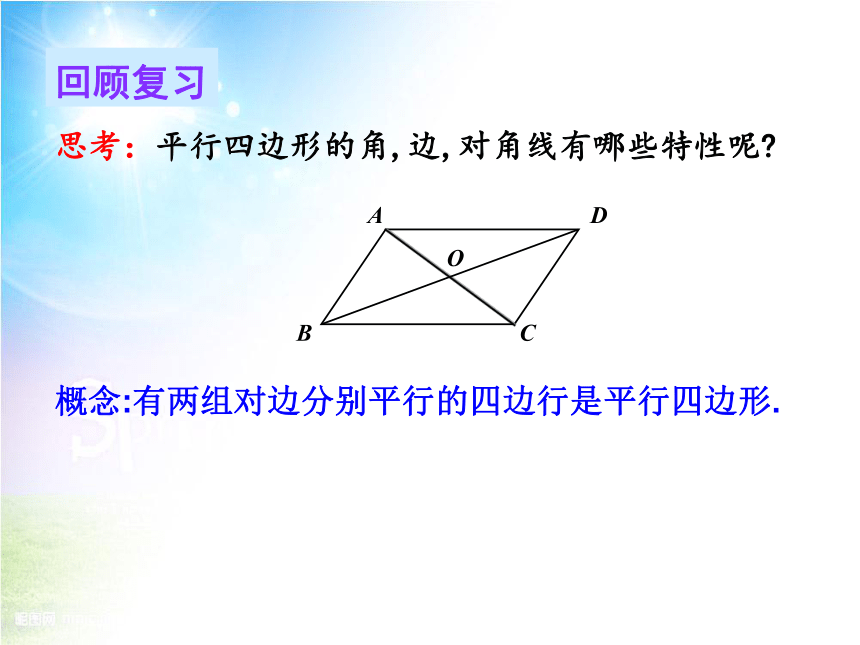
思考:平行四边形的角,边,对角线有哪些特性呢
A
B
C
D
O
概念:有两组对边分别平行的四边行是平行四边形.
回顾复习
进行新课
试
一
试
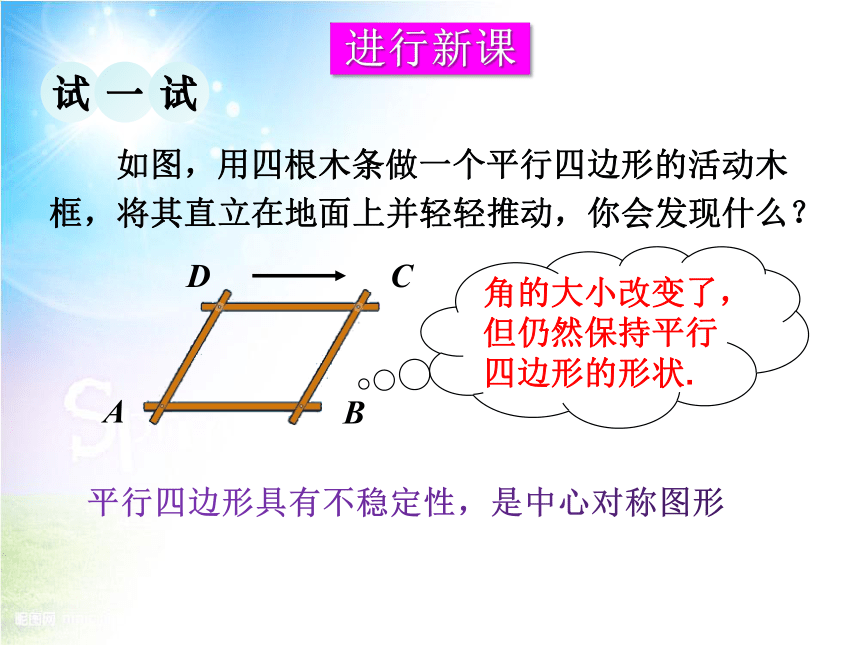
如图,用四根木条做一个平行四边形的活动木框,将其直立在地面上并轻轻推动,你会发现什么?
D
C
B
A
角的大小改变了,但仍然保持平行四边形的形状.
平行四边形具有不稳定性,是中心对称图形
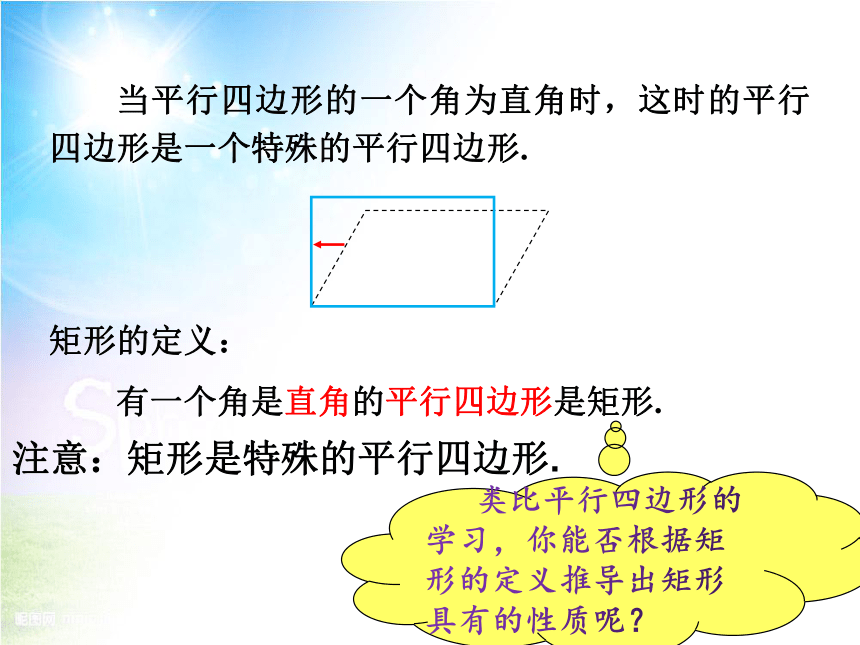
当平行四边形的一个角为直角时,这时的平行四边形是一个特殊的平行四边形.
有一个角是直角的平行四边形是矩形.
矩形的定义:
类比平行四边形的学习,你能否根据矩形的定义推导出矩形具有的性质呢?
注意:矩形是特殊的平行四边形.
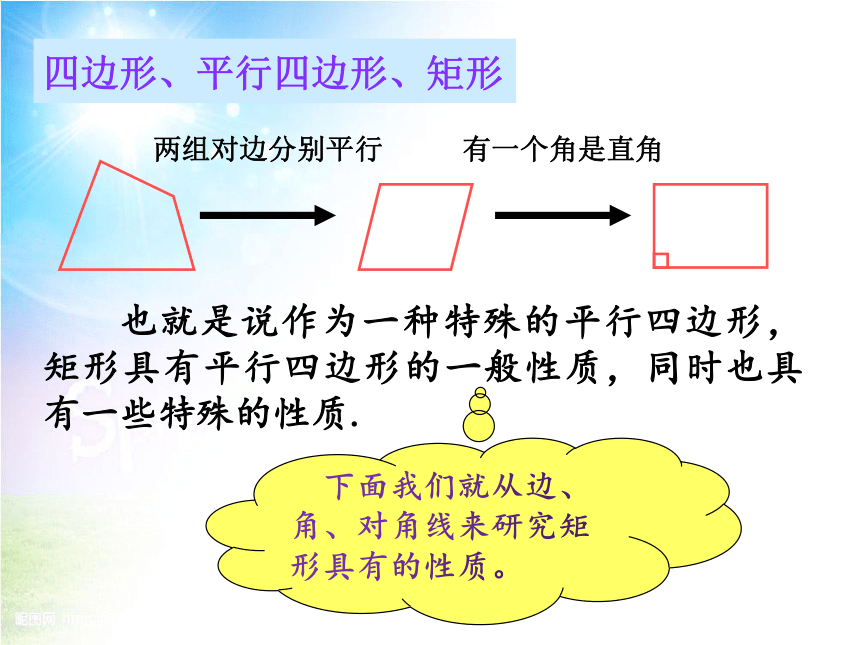
四边形、平行四边形、矩形
两组对边分别平行
有一个角是直角
也就是说作为一种特殊的平行四边形,矩形具有平行四边形的一般性质,同时也具有一些特殊的性质.
下面我们就从边、角、对角线来研究矩形具有的性质。
对称性 边 角 对角线
平行四边形的一般性质
矩形的特殊性质
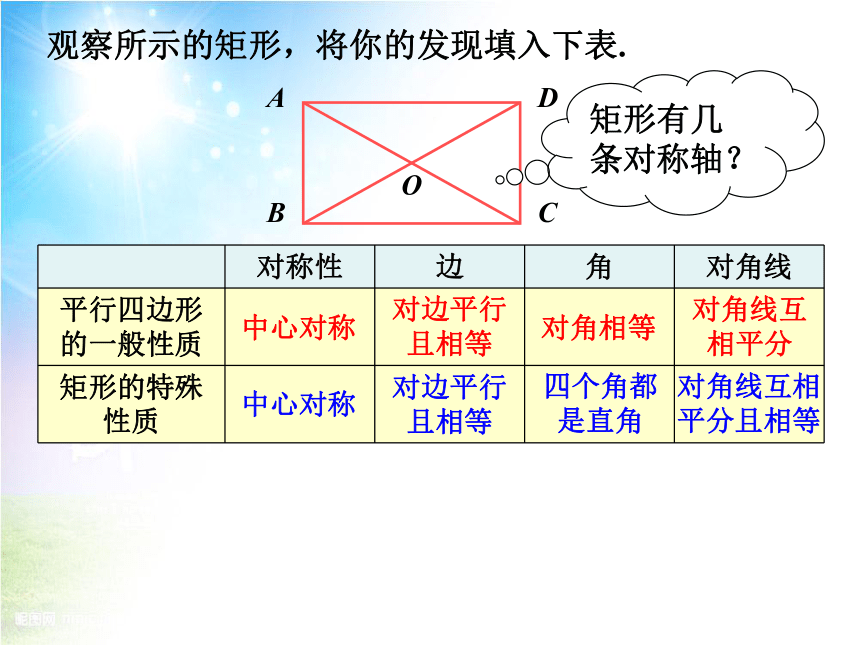
观察所示的矩形,将你的发现填入下表.
A
B
D
C
O
中心对称
对边平行且相等
对角相等
对角线互相平分
中心对称
对边平行且相等
四个角都是直角
对角线互相平分且相等
矩形有几条对称轴?
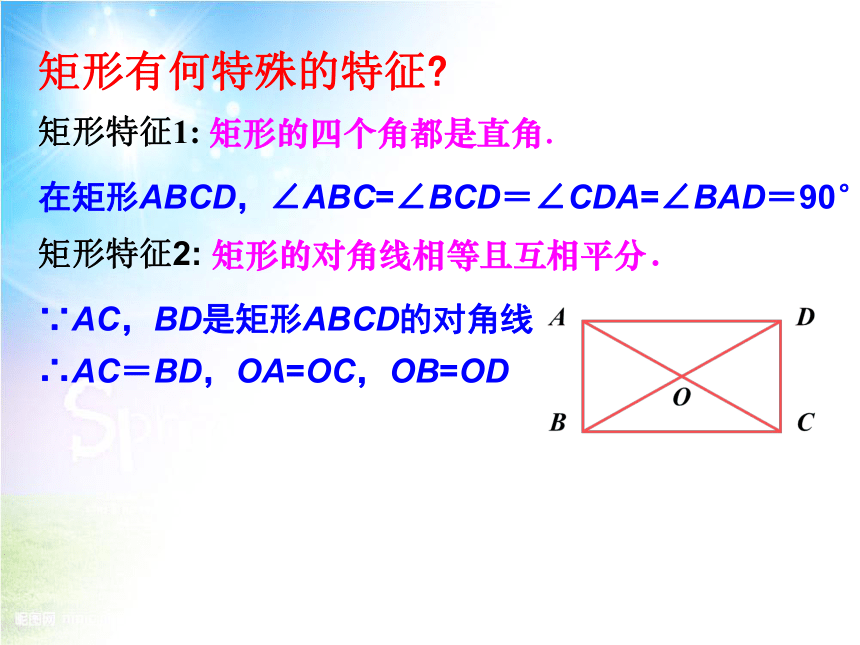
在矩形ABCD,∠ABC=∠BCD=∠CDA=∠BAD=90°
矩形特征2: 矩形的对角线相等且互相平分.
∵AC,BD是矩形ABCD的对角线
∴AC=BD,OA=OC,OB=OD
矩形有何特殊的特征
矩形特征1: 矩形的四个角都是直角.
猜想1:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°
A
B
C
D
证明:
∵四边形ABCD是矩形 ∴ ∠A=90°
又∵矩形ABCD是特殊的平行四边形
∴ ∠A=∠C,∠B = ∠D,∠A +∠B = 180°
∴ ∠A=∠B=∠C=∠D=90°
即矩形的四个角都是直角
已知:如图,四边形ABCD是矩形
求证:AC = BD
A
B
C
D
证明:在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC , BC = CB
∴△ABC≌△DCB (SAS)
∴AC = BD
即矩形的对角线相等
猜想2:矩形的对角线相等
矩形的四个角都是直角.
矩形的两条对角线相等.
从角上看:
从对角线上看:
A
B
C
D
A
B
C
D
符号语言
∵四边形ABCD是矩形
∴∠A=∠B=∠C=∠D=90°
符号语言
∵四边形ABCD是矩形
∴AC = BD
归纳:矩形特有的性质:
1、如图四边形ABCD是矩形
(1)若已知AB=8㎝,AD=6㎝,
则AC=________㎝,OB=________㎝
(2)若已知∠CAB=40°,则∠OCB= ________ ∠OBA=________∠AOB= ________∠AOD=_____.
(3)若已知AC=10㎝,BC=6㎝,则矩形的
周长=________㎝矩形的面积=________㎝2
(4)若已知 ∠DOC=120°,AD=6㎝,
则AC=________㎝
O
D
C
B
A
5
50°
10
100°
40°
12
48
28
80°
小试牛刀
2.矩形ABCD对角线AC,BD相交于点O,AB=5cm,BC=12cm,则△ABO的周长等于 ______ .
3.矩形的两条对角线的夹角为60°,较短的边长为4.5cm,求对角线长.
解:对角线长=2×4.5=9(cm).
小试牛刀
解 在矩形ABCD中,∠ABC=90°,AC= = =5.又∵S△ABC = AB·BC= AC·BE,
∴BE= .
例1 如下图,在矩形ABCD中,AB=3,BC=4,BE⊥AC,垂足为点E.试求BE的长.
A
B
D
C
E
典例讲解
例2 如下图,在矩形ABCD中,对角线AC与BD相交于点O,AE垂直且平分线段BO,垂足为点E,BD=15cm.求AC、AB的长.
典例讲解
A
B
D
C
E
O
解 ∵四边形ABCD是矩形,
∴ AC=BD=15(矩形对角线相等).
∴ AO = AC = 7.5.
∵AE垂直平分BO,∴AB=AO=7.5.
即AC的长为15cm,AB的长为7.5cm.
例3、矩形ABCD的对角线AC,BD相交于点O.
观察Rt△ABC,在Rt△ABC中,BO是斜边AC上
的________,BO与AC有什么关系?
证明:
∵四边形ABCD是矩形,
∴AC=BD,
中线
典例讲解
结论:
直角三角形斜边上的中线等于斜边的一半.
当堂小结
矩形的性质
A
B
C
D
矩形的对边平行且相等.
角
对角线
边
对角线互相平分且相等
四个角都是直角.
对角相等,邻角互补.
对称性
矩形是轴对称图形,
结论:
直角三角形斜边上的中线等于斜边的一半.
矩形问题
通过对角线
转化
直角三角形或等腰三角形
1.矩形ABCD的周长为56cm,对角线AC、BD交于O,△BOC和△AOB的周长差是4cm,那么矩形各边的
长是多少
A
B
C
D
O
解∵AB+BC+CD+DA = 56,
(BC+BO+CO)-(AB+AO+BO)= 4,
又∵四边形ABCD是矩形,
∴AB=CD,AD=BC(平行四边形的对边相等).
AO=CO,BO=DO(平行四边形的对角线互相平分).
∴ AB + BC =28,BC-AB = 4,
∴ AD = BC =16,AB = CD =12.
拓展提高
2.如图,在矩形ABCD中,AC与BD交于O点,BE⊥
AC于E,CF⊥BD于F,求证:BE = CF.
证明:∵AC、BD为矩形ABCD的对角线,∴OB=OC.
又∵∠BEO=∠CFO=90°,∠EOB=∠FOC.
∴Rt△EBO≌Rt△FCO,
∴BE=CF.
拓展提高
19.1 矩 形
1 矩形的性质
第19章 矩形、菱形与正方形
华东师大·八年级数学下册
思考:平行四边形的角,边,对角线有哪些特性呢
A
B
C
D
O
概念:有两组对边分别平行的四边行是平行四边形.
回顾复习
进行新课
试
一
试
如图,用四根木条做一个平行四边形的活动木框,将其直立在地面上并轻轻推动,你会发现什么?
D
C
B
A
角的大小改变了,但仍然保持平行四边形的形状.
平行四边形具有不稳定性,是中心对称图形
当平行四边形的一个角为直角时,这时的平行四边形是一个特殊的平行四边形.
有一个角是直角的平行四边形是矩形.
矩形的定义:
类比平行四边形的学习,你能否根据矩形的定义推导出矩形具有的性质呢?
注意:矩形是特殊的平行四边形.
四边形、平行四边形、矩形
两组对边分别平行
有一个角是直角
也就是说作为一种特殊的平行四边形,矩形具有平行四边形的一般性质,同时也具有一些特殊的性质.
下面我们就从边、角、对角线来研究矩形具有的性质。
对称性 边 角 对角线
平行四边形的一般性质
矩形的特殊性质
观察所示的矩形,将你的发现填入下表.
A
B
D
C
O
中心对称
对边平行且相等
对角相等
对角线互相平分
中心对称
对边平行且相等
四个角都是直角
对角线互相平分且相等
矩形有几条对称轴?
在矩形ABCD,∠ABC=∠BCD=∠CDA=∠BAD=90°
矩形特征2: 矩形的对角线相等且互相平分.
∵AC,BD是矩形ABCD的对角线
∴AC=BD,OA=OC,OB=OD
矩形有何特殊的特征
矩形特征1: 矩形的四个角都是直角.
猜想1:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°
A
B
C
D
证明:
∵四边形ABCD是矩形 ∴ ∠A=90°
又∵矩形ABCD是特殊的平行四边形
∴ ∠A=∠C,∠B = ∠D,∠A +∠B = 180°
∴ ∠A=∠B=∠C=∠D=90°
即矩形的四个角都是直角
已知:如图,四边形ABCD是矩形
求证:AC = BD
A
B
C
D
证明:在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC , BC = CB
∴△ABC≌△DCB (SAS)
∴AC = BD
即矩形的对角线相等
猜想2:矩形的对角线相等
矩形的四个角都是直角.
矩形的两条对角线相等.
从角上看:
从对角线上看:
A
B
C
D
A
B
C
D
符号语言
∵四边形ABCD是矩形
∴∠A=∠B=∠C=∠D=90°
符号语言
∵四边形ABCD是矩形
∴AC = BD
归纳:矩形特有的性质:
1、如图四边形ABCD是矩形
(1)若已知AB=8㎝,AD=6㎝,
则AC=________㎝,OB=________㎝
(2)若已知∠CAB=40°,则∠OCB= ________ ∠OBA=________∠AOB= ________∠AOD=_____.
(3)若已知AC=10㎝,BC=6㎝,则矩形的
周长=________㎝矩形的面积=________㎝2
(4)若已知 ∠DOC=120°,AD=6㎝,
则AC=________㎝
O
D
C
B
A
5
50°
10
100°
40°
12
48
28
80°
小试牛刀
2.矩形ABCD对角线AC,BD相交于点O,AB=5cm,BC=12cm,则△ABO的周长等于 ______ .
3.矩形的两条对角线的夹角为60°,较短的边长为4.5cm,求对角线长.
解:对角线长=2×4.5=9(cm).
小试牛刀
解 在矩形ABCD中,∠ABC=90°,AC= = =5.又∵S△ABC = AB·BC= AC·BE,
∴BE= .
例1 如下图,在矩形ABCD中,AB=3,BC=4,BE⊥AC,垂足为点E.试求BE的长.
A
B
D
C
E
典例讲解
例2 如下图,在矩形ABCD中,对角线AC与BD相交于点O,AE垂直且平分线段BO,垂足为点E,BD=15cm.求AC、AB的长.
典例讲解
A
B
D
C
E
O
解 ∵四边形ABCD是矩形,
∴ AC=BD=15(矩形对角线相等).
∴ AO = AC = 7.5.
∵AE垂直平分BO,∴AB=AO=7.5.
即AC的长为15cm,AB的长为7.5cm.
例3、矩形ABCD的对角线AC,BD相交于点O.
观察Rt△ABC,在Rt△ABC中,BO是斜边AC上
的________,BO与AC有什么关系?
证明:
∵四边形ABCD是矩形,
∴AC=BD,
中线
典例讲解
结论:
直角三角形斜边上的中线等于斜边的一半.
当堂小结
矩形的性质
A
B
C
D
矩形的对边平行且相等.
角
对角线
边
对角线互相平分且相等
四个角都是直角.
对角相等,邻角互补.
对称性
矩形是轴对称图形,
结论:
直角三角形斜边上的中线等于斜边的一半.
矩形问题
通过对角线
转化
直角三角形或等腰三角形
1.矩形ABCD的周长为56cm,对角线AC、BD交于O,△BOC和△AOB的周长差是4cm,那么矩形各边的
长是多少
A
B
C
D
O
解∵AB+BC+CD+DA = 56,
(BC+BO+CO)-(AB+AO+BO)= 4,
又∵四边形ABCD是矩形,
∴AB=CD,AD=BC(平行四边形的对边相等).
AO=CO,BO=DO(平行四边形的对角线互相平分).
∴ AB + BC =28,BC-AB = 4,
∴ AD = BC =16,AB = CD =12.
拓展提高
2.如图,在矩形ABCD中,AC与BD交于O点,BE⊥
AC于E,CF⊥BD于F,求证:BE = CF.
证明:∵AC、BD为矩形ABCD的对角线,∴OB=OC.
又∵∠BEO=∠CFO=90°,∠EOB=∠FOC.
∴Rt△EBO≌Rt△FCO,
∴BE=CF.
拓展提高
