华师大版数学八下 19.1.2矩形的判定 课件(共16张PPT)
文档属性
| 名称 | 华师大版数学八下 19.1.2矩形的判定 课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 628.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-24 17:39:40 | ||
图片预览





文档简介
(共16张PPT)
19.1.2 矩形的判定
华东师大·八年级数学下册
第19章 矩形、菱形与正方形
复习导入
回顾复习
有一个角是直角的平行四边形叫做矩形.
有一个角是直角
矩形的两条对角线相等且互相平分.
矩形的性质
边:
矩形的对边平行且相等.
角:
矩形的四个角都是直角.
对角线:
说出上述命题的逆命题?由此你可以得到矩形的判定有哪些?
已知:在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
证明:
∵ ∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°.
∴AD∥BC,AB∥CD.
∴四边形ABCD是平行四边形.
∴四边形ABCD是矩形(有一个角是直角的平行四边形是矩形).
命题1、有三个角是直角的四边形是矩形.
已知:在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
矩形的判定定理1 有三个角是直角的四边形是矩形.
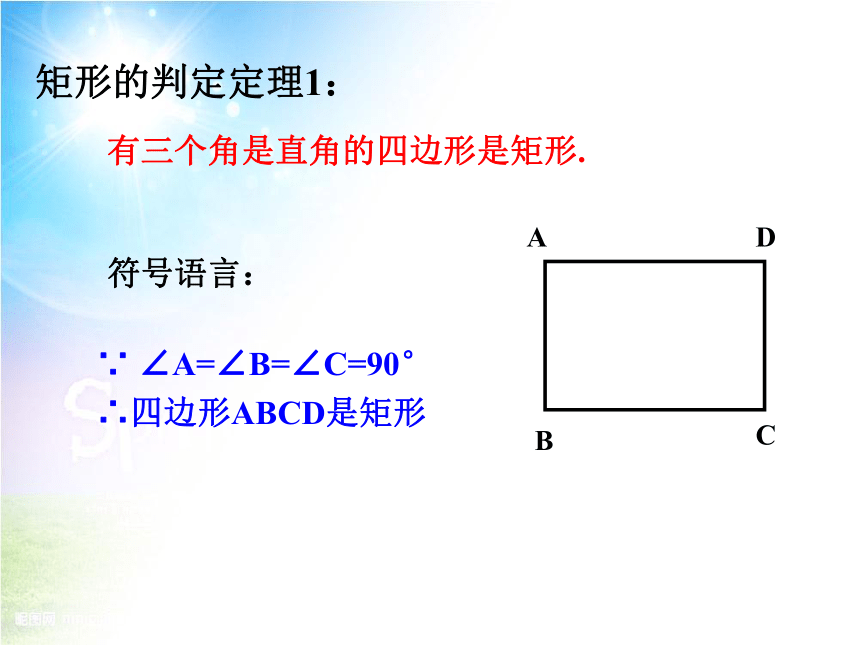
矩形的判定定理1:
有三个角是直角的四边形是矩形.
A
B
C
D
∵ ∠A=∠B=∠C=90°
∴四边形ABCD是矩形
符号语言:
命题2、对角线相等的平行四边形是矩形.
已知:四边形ABCD是平行四边形,AC=DB.
求证:四边形ABCD是矩形.
证明:
∵ 四边形ABCD是平行四边形,
∴AB=DC,∴∠ABC+∠DCB=180°.
∴∠ABC=∠DCB=90°.
又∵AC=DB,BC=CB,∴△ABC≌△DCB,
∴四边形ABCD是矩形(有一个角是直角的平行四边形是矩形).
∥
符号语言:
∵四边形ABCD是平行四边形
且AC=BD
∴四边形ABCD是矩形
(或OA=OC=OB=OD)
矩形的判定定理2 对角线相等的平行四边形是矩形.
对角线相等的平行四边形是矩形 。
(对角线相等且互相平分的四边形是矩形。)
有三个角是直角的四边形是矩形 。
方法2:
方法3:
归纳矩形的判定方法:
有一个角是直角的平行四边形是矩形。
方法1:(定义)
小试牛刀
2.在四边形ABCD中,AC、BD交于点O,在下列各组
条件中,不能判定四边形ABCD为矩形的是( )
A.AB=CD,AD=BC,AC=BD
B.AO=CO,BO=DO,∠A=90°
C.∠A=∠C,∠B+∠C=180°,AC⊥BD
D.∠A=∠B=90°,AC=BD
C
小试牛刀
1.下列判定矩形的说法是否正确?为什么?
(1)有一个角是直角的四边形是矩形.( )
(2)四个角都相等的四边形是矩形. ( )
(3)对角线相等的四边形是矩形. ( )
(4)对角线互相平分,且有一个角是直角的四边形是矩形. ( )
×
√
×
√
×
√
×
例1 如图,点O是矩形ABCD的对角线AC与BD的交点,E、F、G、H分别是AO、BO、CO、DO上的一点,且AE=BF=CG=DH.求证四边形EFGH是矩形.
证明:
∵ 四边形ABCD是矩形,
∴AO=BO=CO=DO.
∴OE=OF=OG=OH,
∵AE=BF=CG=DH,
∴四边形EFGH是平行四边形.
∵EO+OG=FO+OH,即EG=FH,
∴四边形EFGH是矩形(对角线相等的平行四边形是矩形).
A
B
D
C
O
E
H
G
F
典例讲解
例2 如图,四边形ABCD是由两个全等的正三角形ABD和BCD组成的,M、N分别为BC、AD的中点.求证:四边形BMDN是矩形.
D
B
A
N
M
C
证明:
∵ △ABD和△BCD是全等三角形,
∴∠ADB=∠CDB=60°.
∴BN⊥AD,DM⊥BC,∠BDM=30°,
又∵M、N分别为BC、AD的中点,
∴∠DNB=∠DMB=90°,
∠MDN=∠ADB+∠BDM=90°
∴四边形BMDN是矩形(有三个角是直角的四边形是矩形).
典例讲解
例3 如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AG是△ABC的外角∠FAC的平分线,DE∥AB,交AG于点E.求证:四边形ADCE是矩形.
A
B
D
C
E
G
F
1
2
证明:
∵ AB=AC,AD⊥BC
∴∠B=∠ACB,BD=DC.
∴∠1= ∠CAF= (∠B+∠ACB)=∠B,
又∵AE是△ABC的外角∠CAF的平分线,
∴AE∥BC.又∵AB∥DE,
∴四边形ABDE是平行四边形.
∴AE=BD,AB=DE,∴AC=DE,AE=DC.
又∵AE∥DC,∴四边形ADCE是平行四边形.
∴四边形ADCE是矩形(对角线相等的平行四边形是矩形).
典例讲解
证明:
∴AE∥BC.又∵AB∥DE,
当堂小结
对角线相等的平行四边形是矩形.
有一个角是直角的平行四边形是矩形.
有三个角是直角的四边形是矩形.
矩形的判定定理
1. 已知平行四边形ABCD的对角线AC,BD交于点O,△AOB是等边三角形,AB=4cm.
(1)这个平行四边形是矩形吗?说明你的理由;
(2)求这个平行四边形的面积.
解:(1)是.∵△AOB是等边三角形,∴AO=BO,
又∵AO = AC,BO = BD.
(平行四边形的性质)
∴AC=BD.
∴ ABCD是矩形.
(2)S ABCD= (cm2)
拓展提高
2.如图,在△ABC中,D在AB边上,AD=BD=CD,DE∥AC,DF∥BC.求证:四边形DECF是矩形.
证明:∵AD=BD=CD,
∴△ABC为直角三角形,∠FCE=90°
∵DE∥AC,DF∥BC,
∴四边形DECF为平行四边形,
又∵∠FCE=90°,
∴平行四边形DECF是矩形.
拓展提高
19.1.2 矩形的判定
华东师大·八年级数学下册
第19章 矩形、菱形与正方形
复习导入
回顾复习
有一个角是直角的平行四边形叫做矩形.
有一个角是直角
矩形的两条对角线相等且互相平分.
矩形的性质
边:
矩形的对边平行且相等.
角:
矩形的四个角都是直角.
对角线:
说出上述命题的逆命题?由此你可以得到矩形的判定有哪些?
已知:在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
证明:
∵ ∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°.
∴AD∥BC,AB∥CD.
∴四边形ABCD是平行四边形.
∴四边形ABCD是矩形(有一个角是直角的平行四边形是矩形).
命题1、有三个角是直角的四边形是矩形.
已知:在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
矩形的判定定理1 有三个角是直角的四边形是矩形.
矩形的判定定理1:
有三个角是直角的四边形是矩形.
A
B
C
D
∵ ∠A=∠B=∠C=90°
∴四边形ABCD是矩形
符号语言:
命题2、对角线相等的平行四边形是矩形.
已知:四边形ABCD是平行四边形,AC=DB.
求证:四边形ABCD是矩形.
证明:
∵ 四边形ABCD是平行四边形,
∴AB=DC,∴∠ABC+∠DCB=180°.
∴∠ABC=∠DCB=90°.
又∵AC=DB,BC=CB,∴△ABC≌△DCB,
∴四边形ABCD是矩形(有一个角是直角的平行四边形是矩形).
∥
符号语言:
∵四边形ABCD是平行四边形
且AC=BD
∴四边形ABCD是矩形
(或OA=OC=OB=OD)
矩形的判定定理2 对角线相等的平行四边形是矩形.
对角线相等的平行四边形是矩形 。
(对角线相等且互相平分的四边形是矩形。)
有三个角是直角的四边形是矩形 。
方法2:
方法3:
归纳矩形的判定方法:
有一个角是直角的平行四边形是矩形。
方法1:(定义)
小试牛刀
2.在四边形ABCD中,AC、BD交于点O,在下列各组
条件中,不能判定四边形ABCD为矩形的是( )
A.AB=CD,AD=BC,AC=BD
B.AO=CO,BO=DO,∠A=90°
C.∠A=∠C,∠B+∠C=180°,AC⊥BD
D.∠A=∠B=90°,AC=BD
C
小试牛刀
1.下列判定矩形的说法是否正确?为什么?
(1)有一个角是直角的四边形是矩形.( )
(2)四个角都相等的四边形是矩形. ( )
(3)对角线相等的四边形是矩形. ( )
(4)对角线互相平分,且有一个角是直角的四边形是矩形. ( )
×
√
×
√
×
√
×
例1 如图,点O是矩形ABCD的对角线AC与BD的交点,E、F、G、H分别是AO、BO、CO、DO上的一点,且AE=BF=CG=DH.求证四边形EFGH是矩形.
证明:
∵ 四边形ABCD是矩形,
∴AO=BO=CO=DO.
∴OE=OF=OG=OH,
∵AE=BF=CG=DH,
∴四边形EFGH是平行四边形.
∵EO+OG=FO+OH,即EG=FH,
∴四边形EFGH是矩形(对角线相等的平行四边形是矩形).
A
B
D
C
O
E
H
G
F
典例讲解
例2 如图,四边形ABCD是由两个全等的正三角形ABD和BCD组成的,M、N分别为BC、AD的中点.求证:四边形BMDN是矩形.
D
B
A
N
M
C
证明:
∵ △ABD和△BCD是全等三角形,
∴∠ADB=∠CDB=60°.
∴BN⊥AD,DM⊥BC,∠BDM=30°,
又∵M、N分别为BC、AD的中点,
∴∠DNB=∠DMB=90°,
∠MDN=∠ADB+∠BDM=90°
∴四边形BMDN是矩形(有三个角是直角的四边形是矩形).
典例讲解
例3 如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AG是△ABC的外角∠FAC的平分线,DE∥AB,交AG于点E.求证:四边形ADCE是矩形.
A
B
D
C
E
G
F
1
2
证明:
∵ AB=AC,AD⊥BC
∴∠B=∠ACB,BD=DC.
∴∠1= ∠CAF= (∠B+∠ACB)=∠B,
又∵AE是△ABC的外角∠CAF的平分线,
∴AE∥BC.又∵AB∥DE,
∴四边形ABDE是平行四边形.
∴AE=BD,AB=DE,∴AC=DE,AE=DC.
又∵AE∥DC,∴四边形ADCE是平行四边形.
∴四边形ADCE是矩形(对角线相等的平行四边形是矩形).
典例讲解
证明:
∴AE∥BC.又∵AB∥DE,
当堂小结
对角线相等的平行四边形是矩形.
有一个角是直角的平行四边形是矩形.
有三个角是直角的四边形是矩形.
矩形的判定定理
1. 已知平行四边形ABCD的对角线AC,BD交于点O,△AOB是等边三角形,AB=4cm.
(1)这个平行四边形是矩形吗?说明你的理由;
(2)求这个平行四边形的面积.
解:(1)是.∵△AOB是等边三角形,∴AO=BO,
又∵AO = AC,BO = BD.
(平行四边形的性质)
∴AC=BD.
∴ ABCD是矩形.
(2)S ABCD= (cm2)
拓展提高
2.如图,在△ABC中,D在AB边上,AD=BD=CD,DE∥AC,DF∥BC.求证:四边形DECF是矩形.
证明:∵AD=BD=CD,
∴△ABC为直角三角形,∠FCE=90°
∵DE∥AC,DF∥BC,
∴四边形DECF为平行四边形,
又∵∠FCE=90°,
∴平行四边形DECF是矩形.
拓展提高
