江苏省江都市大桥高中2012-2013学年高一下学期开学考试数学试题
文档属性
| 名称 | 江苏省江都市大桥高中2012-2013学年高一下学期开学考试数学试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 317.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | |||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-07 00:00:00 | ||
图片预览

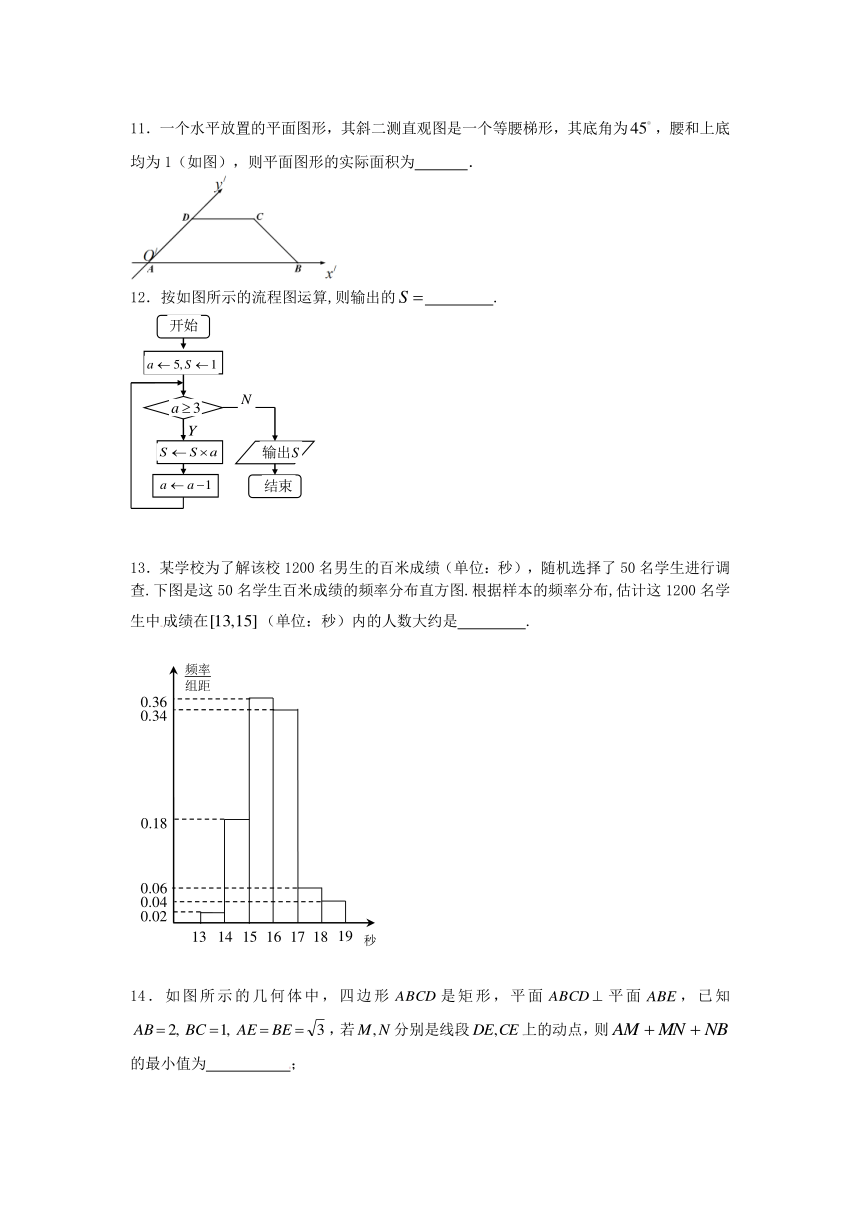

文档简介
江都市大桥高中2012-2013学年度高一下学期开学考试
数学试题
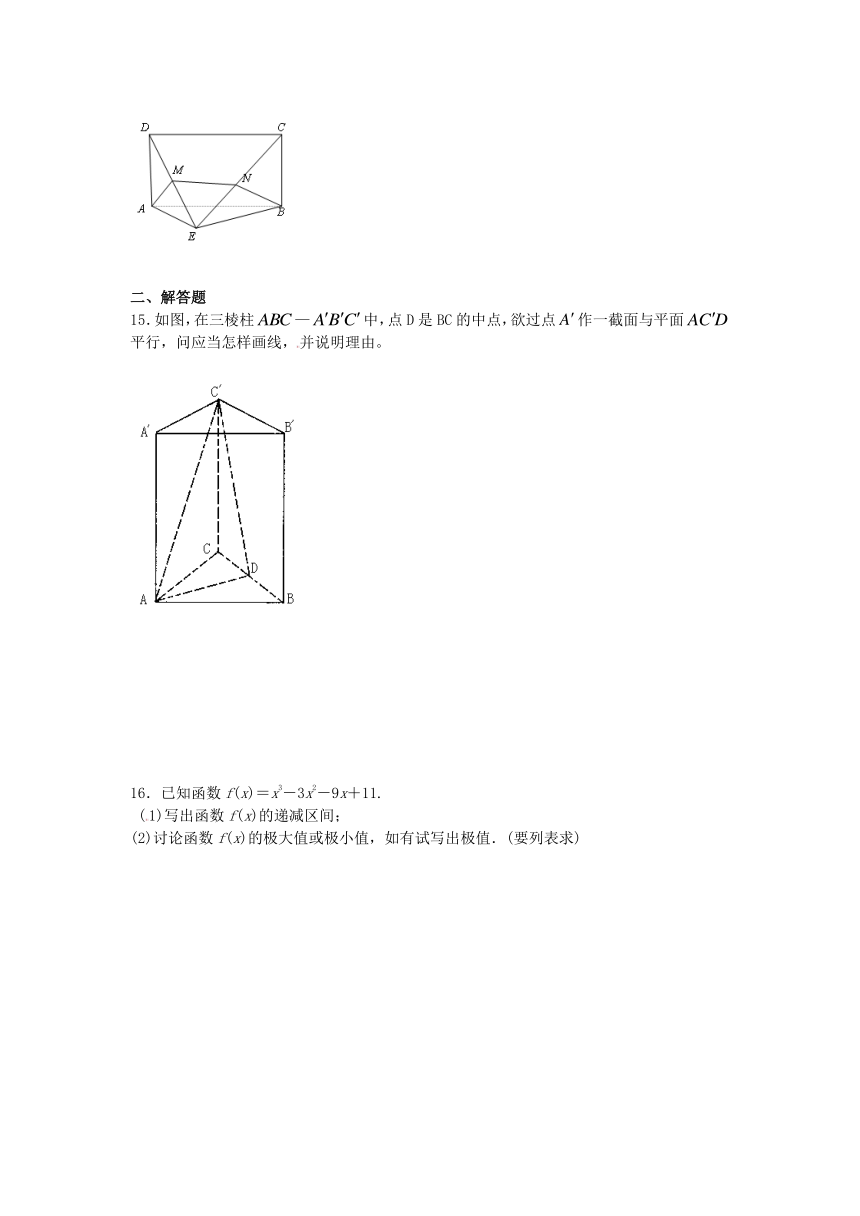
一、填空题
1.不等式的解集为_______________.
2.已知向量,,若向量,则____________
3.数列中,恰好有5个,2个,则不相同的数列共有 个.
4.给出以下变量①吸烟,②性别,③宗教信仰,④国籍
其中属于分类变量的有________
5.对于函数若存在,使成立,则称点为函数的不动点,对于任意实数,函数总有相异不动点,实数的取值范围是____
6.已知△ABC中,角A、B、C的对边分别为,且,那么 .
7.在中,,,,则
8.、如图,将边长为1的正六边形铁皮的六个角各切去一个全等的四边形,再沿虚线折成一个无盖的正六棱柱容器,当容器底边长为 时,容积最大。
9.函数在区间[—2,3]上的最大值为 。
10.如图,四边形中,,,.将四边形沿对角线折成四面体,使平面⊥平面,则与平面所成的角的正弦值为 .
11.一个水平放置的平面图形,其斜二测直观图是一个等腰梯形,其底角为,腰和上底均为1(如图),则平面图形的实际面积为 .
12.按如图所示的流程图运算,则输出的 .
13.某学校为了解该校1200名男生的百米成绩(单位:秒),随机选择了50名学生进行调查.下图是这50名学生百米成绩的频率分布直方图.根据样本的频率分布,估计这1200名学生中成绩在(单位:秒)内的人数大约是 .
14.如图所示的几何体中,四边形是矩形,平面平面,已知,若分别是线段上的动点,则的最小值为 ;
二、解答题
15.如图,在三棱柱—中,点D是BC的中点,欲过点作一截面与平面平行,问应当怎样画线,并说明理由。
16.已知函数f(x)=x3-3x2-9x+11.
(1)写出函数f(x)的递减区间;
(2)讨论函数f(x)的极大值或极小值,如有试写出极值.(要列表求)
17.对于函数:
(Ⅰ) 是否存在实数使函数为奇函数?
(Ⅱ) 探究函数的单调性(不用证明),并求出函数的值域.
18.如图组合体中,三棱柱的侧面是圆柱的轴截面,是圆柱底面圆周上不与重合一个点。
(Ⅰ)求证:无论点如何运动,平面平面;
(Ⅱ)当点是弧的中点时,求四棱锥与圆柱的体积比。
19.已知二次函数,若不等式的解集为,且方程有两个相等的实数根.(1)求的解析式;(2)若不等式在上恒成立,求实数的取值范围;
20.已知函数在处取得极大值.
(Ⅰ)求在区间上的最大值;
(Ⅱ)若过点可作曲线的切线有三条,求实数的取值范围.
参考答案
1.(– 1,1)
2.-8
3.21
4.②③④
5.
6.
7.
8. 2/3
9.72
10.
11.
12.60
13.240
14.3
15.解:(Ⅰ)取的中点E,连结,
则平面∥平面……………………4分
∵D为BC的中点,E为的中点,∴
又∵BC∥,∴四边形为平行四边形,
∴∥BE,……………………………………7分
连结DE,则DE,
∴DE,
∴四边形是平行四边形,
∴AD∥……………………………………………………………10分
又∵ 平面,,∴平面∥平面。………12分
16.f′(x)=3x2-6x-9=3 (x+1)(x-3),
令f′(x)=0,得x1=-1,x2=3.
x变化时,f′(x)的符号变化情况及f(x)的增减性如下表所示:
x
(-∞,-1)
-1
(-1,3)
3
(3,+∞)
f′(x)
+
0
-
0
+
f(x)
增
极大值
f(-1)
减
极小值
f(3)
增
17.解:(Ⅰ)(解法一)假设存在实数函数是奇函数,因为的定义域为,
所以,所以……………2分
此时,则,所以为奇函数
即存在实数使函数为奇函数.……………5分
(解法二)假设存在实数使函数为奇函数,即有
即,……………2分
所以
所以,即存在实数使函数为奇函数.……………5分
(Ⅱ)由(Ⅰ)知,因为在上递增,所以在上递减,所以在上递增.…………………8分
,,
即函数的值域为.……………12分
18.(1)见解析(2)
(Ⅰ)因为侧面是圆柱的的轴截面,是圆柱底面圆周上不与、重合一个点,所以
又圆柱母线?平面,平面,所以,
又,所以?平面,
因为平面,所以平面平面;
(Ⅱ)设圆柱的底面半径为,母线长为,当点是弧的中点时,三角形的面积为,三棱柱的体积为,三棱锥的体积为,四棱锥的体积为,
圆柱的体积为,四棱锥与圆柱的体积比为
19.(1);
(2) 。
试题分析:(1)由不等式的解集为,可知,再根据有两个相等的实数根,
利用韦达定理及判别式可建立关于a,b的三个方程,还要注意a取正整数.
从而得到a,b,c的值.
(2)由,然后分离常数可转化为恒成立,从而转化为求的最值,再利用基本不等式求解即可.
(1)由题意..........3分
.............6分
....8分
(2)
......16分
考点:三个“二次”之间的关系,不等式恒成立问题,基本不等式求最偷.
点评:解本小题的关键是根据一元二次不等式的解集得到对应方程的根,从而得到a,b,c的值.对于不等式恒成立问题,在变量与参数能分离的情况下,转化为函数最值来研究.
20.(Ⅰ)
当
故满足条件的的取值范围
数学试题
一、填空题
1.不等式的解集为_______________.
2.已知向量,,若向量,则____________
3.数列中,恰好有5个,2个,则不相同的数列共有 个.
4.给出以下变量①吸烟,②性别,③宗教信仰,④国籍
其中属于分类变量的有________
5.对于函数若存在,使成立,则称点为函数的不动点,对于任意实数,函数总有相异不动点,实数的取值范围是____
6.已知△ABC中,角A、B、C的对边分别为,且,那么 .
7.在中,,,,则
8.、如图,将边长为1的正六边形铁皮的六个角各切去一个全等的四边形,再沿虚线折成一个无盖的正六棱柱容器,当容器底边长为 时,容积最大。
9.函数在区间[—2,3]上的最大值为 。
10.如图,四边形中,,,.将四边形沿对角线折成四面体,使平面⊥平面,则与平面所成的角的正弦值为 .
11.一个水平放置的平面图形,其斜二测直观图是一个等腰梯形,其底角为,腰和上底均为1(如图),则平面图形的实际面积为 .
12.按如图所示的流程图运算,则输出的 .
13.某学校为了解该校1200名男生的百米成绩(单位:秒),随机选择了50名学生进行调查.下图是这50名学生百米成绩的频率分布直方图.根据样本的频率分布,估计这1200名学生中成绩在(单位:秒)内的人数大约是 .
14.如图所示的几何体中,四边形是矩形,平面平面,已知,若分别是线段上的动点,则的最小值为 ;
二、解答题
15.如图,在三棱柱—中,点D是BC的中点,欲过点作一截面与平面平行,问应当怎样画线,并说明理由。
16.已知函数f(x)=x3-3x2-9x+11.
(1)写出函数f(x)的递减区间;
(2)讨论函数f(x)的极大值或极小值,如有试写出极值.(要列表求)
17.对于函数:
(Ⅰ) 是否存在实数使函数为奇函数?
(Ⅱ) 探究函数的单调性(不用证明),并求出函数的值域.
18.如图组合体中,三棱柱的侧面是圆柱的轴截面,是圆柱底面圆周上不与重合一个点。
(Ⅰ)求证:无论点如何运动,平面平面;
(Ⅱ)当点是弧的中点时,求四棱锥与圆柱的体积比。
19.已知二次函数,若不等式的解集为,且方程有两个相等的实数根.(1)求的解析式;(2)若不等式在上恒成立,求实数的取值范围;
20.已知函数在处取得极大值.
(Ⅰ)求在区间上的最大值;
(Ⅱ)若过点可作曲线的切线有三条,求实数的取值范围.
参考答案
1.(– 1,1)
2.-8
3.21
4.②③④
5.
6.
7.
8. 2/3
9.72
10.
11.
12.60
13.240
14.3
15.解:(Ⅰ)取的中点E,连结,
则平面∥平面……………………4分
∵D为BC的中点,E为的中点,∴
又∵BC∥,∴四边形为平行四边形,
∴∥BE,……………………………………7分
连结DE,则DE,
∴DE,
∴四边形是平行四边形,
∴AD∥……………………………………………………………10分
又∵ 平面,,∴平面∥平面。………12分
16.f′(x)=3x2-6x-9=3 (x+1)(x-3),
令f′(x)=0,得x1=-1,x2=3.
x变化时,f′(x)的符号变化情况及f(x)的增减性如下表所示:
x
(-∞,-1)
-1
(-1,3)
3
(3,+∞)
f′(x)
+
0
-
0
+
f(x)
增
极大值
f(-1)
减
极小值
f(3)
增
17.解:(Ⅰ)(解法一)假设存在实数函数是奇函数,因为的定义域为,
所以,所以……………2分
此时,则,所以为奇函数
即存在实数使函数为奇函数.……………5分
(解法二)假设存在实数使函数为奇函数,即有
即,……………2分
所以
所以,即存在实数使函数为奇函数.……………5分
(Ⅱ)由(Ⅰ)知,因为在上递增,所以在上递减,所以在上递增.…………………8分
,,
即函数的值域为.……………12分
18.(1)见解析(2)
(Ⅰ)因为侧面是圆柱的的轴截面,是圆柱底面圆周上不与、重合一个点,所以
又圆柱母线?平面,平面,所以,
又,所以?平面,
因为平面,所以平面平面;
(Ⅱ)设圆柱的底面半径为,母线长为,当点是弧的中点时,三角形的面积为,三棱柱的体积为,三棱锥的体积为,四棱锥的体积为,
圆柱的体积为,四棱锥与圆柱的体积比为
19.(1);
(2) 。
试题分析:(1)由不等式的解集为,可知,再根据有两个相等的实数根,
利用韦达定理及判别式可建立关于a,b的三个方程,还要注意a取正整数.
从而得到a,b,c的值.
(2)由,然后分离常数可转化为恒成立,从而转化为求的最值,再利用基本不等式求解即可.
(1)由题意..........3分
.............6分
....8分
(2)
......16分
考点:三个“二次”之间的关系,不等式恒成立问题,基本不等式求最偷.
点评:解本小题的关键是根据一元二次不等式的解集得到对应方程的根,从而得到a,b,c的值.对于不等式恒成立问题,在变量与参数能分离的情况下,转化为函数最值来研究.
20.(Ⅰ)
当
故满足条件的的取值范围
同课章节目录
