必修二第一章 球的表面积和体积
文档属性
| 名称 | 必修二第一章 球的表面积和体积 |

|
|
| 格式 | zip | ||
| 文件大小 | 993.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-07 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
问题提出
1.柱体、锥体、台体的体积公式分别是什么?圆柱、圆锥、圆台的表面积和体积公式分别是什么?
2.球是一个旋转体,它也有表面积和体积,怎样求一个球的表面积和体积也就成为我们学习的内容.
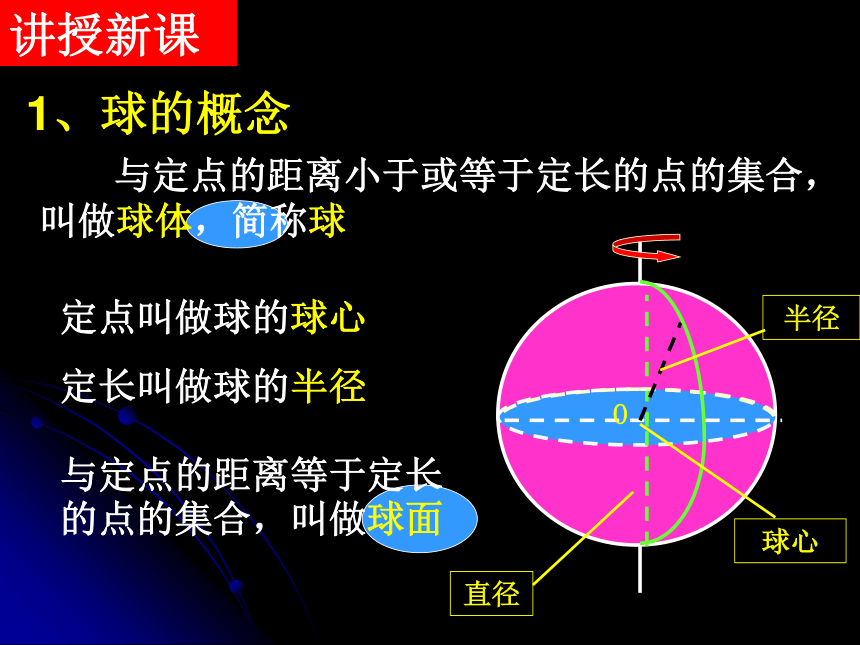
与定点的距离小于或等于定长的点的集合,叫做球体,简称球
讲授新课
1、球的概念
定点叫做球的球心
定长叫做球的半径
与定点的距离等于定长的点的集合,叫做球面
O
半径
球心
直径
2、 球的表面积
o
思考:经过球心的截面圆面积是什么?它与球的表面积有什么关系?
定理:半径为R的球的表面积是
球的表面积等于球的大圆面积的4倍
3、 球的体积
定理:半径为R的球的体积是
例1、地球和火星都可以看作近似球体,地球半径约为6370km,火星的直径约为地球的一半。
求地球的表面积和体积;
火星的表面积约为地球表面积的几分之几?体积呢?
解:
(1)
(2)
例2、如图,圆柱的底面直径与高都等于球的直径,求证:
(1)球的表面积等于圆柱的侧面积.
(2)球的表面积等于圆柱全面积的三分之二.
O
证明:
R
(1)设球的半径为R,
得:
则圆柱的底面半径为R,高为2R.
(2)
2
2
2
6
2
4
R
R
R
S
p
p
p
=
+
=
圆柱全
Q
4.若两球体积之比是1:2,则其表面积之比是______.
练习一
1.若球的表面积变为原来的2倍,则半径变为原来的___倍.
2.若球半径变为原来的2倍,则表面积变为原来的___倍.
3.若两球表面积之比为1:2,则其体积之比是______.
课堂练习
6.将半径为1和2的两个铅球,熔成一个大铅球,那么
这个大铅球的表面积是______.
5.若两球表面积之差为48π ,它们大圆周长之和为12π ,
则两球的直径之差为______.
练习二
课堂练习
例3.钢球直径是5cm,求它的体积和表面积.
(变式1)一种空心钢球的质量是142g,外径是5cm,求它的内径.(钢的密度是7.9g/cm2)
解:设空心钢球的内径为2xcm,则钢球的质量是
答:空心钢球的内径约为4.5cm.
“内径”是指内壁的直径,“外径”是指外壁直径。
(变式2)把直径为5cm钢球放入一个正方体的有盖纸盒中,至少要用多少纸
解:当球内切于正方体时用料最省时
此时棱长=直径=5cm
答:至少要用纸150cm2
两个几何体相切:一个几何体的各个面与另一个几何体的各面相切.
分析:用料最省时,球与正方体有什么位置关系
球内切于正方体
例4.如图,正方体的棱长为a,它的各个顶点都在球的球面上,求球的表面积和体积。
分析:正方体内接于球,则由球和正方体都是中心对称图形可知,它们中心重合,则正方体对角线与球的直径相等。
两个几何体相接:一个几何体的所有顶点都 在另一个几何体的表面上。
(变式) 球的内接长方体的长、宽、高分别为3、2、 ,求此球体的表面积和体积。
分析:长方体内接于球,则由球和长方体都是中心对称图形可知,它们中心重合,则长方体对角线与球的直径相等。
例5、如图是一个奖杯的三视图,单位是cm,
试画出它的直观图,并计算这个奖杯的体积.
(精确到0.01cm)
8
6
6
18
5
15
15
11
11
x/
y/
z/
解:这个奖杯的体积为
V=V正四棱台+V长方体+ V球
其中
V正四棱台
V长方体=6×8×18=864
V球=
所以这个奖杯的体积为
V ≈ 1828.76(cm3)
小结:
(1)有关球和球面的概念。
(2)球的体积公式:
球的表面积公式:
(3)球的体积公式和表面积的一些运用。
(4)多面体的“切”、“接”问题,必须明确“切”、“接”位置和有关元素间的数量关系,常借助“截面”图形来解决。
问题提出
1.柱体、锥体、台体的体积公式分别是什么?圆柱、圆锥、圆台的表面积和体积公式分别是什么?
2.球是一个旋转体,它也有表面积和体积,怎样求一个球的表面积和体积也就成为我们学习的内容.
与定点的距离小于或等于定长的点的集合,叫做球体,简称球
讲授新课
1、球的概念
定点叫做球的球心
定长叫做球的半径
与定点的距离等于定长的点的集合,叫做球面
O
半径
球心
直径
2、 球的表面积
o
思考:经过球心的截面圆面积是什么?它与球的表面积有什么关系?
定理:半径为R的球的表面积是
球的表面积等于球的大圆面积的4倍
3、 球的体积
定理:半径为R的球的体积是
例1、地球和火星都可以看作近似球体,地球半径约为6370km,火星的直径约为地球的一半。
求地球的表面积和体积;
火星的表面积约为地球表面积的几分之几?体积呢?
解:
(1)
(2)
例2、如图,圆柱的底面直径与高都等于球的直径,求证:
(1)球的表面积等于圆柱的侧面积.
(2)球的表面积等于圆柱全面积的三分之二.
O
证明:
R
(1)设球的半径为R,
得:
则圆柱的底面半径为R,高为2R.
(2)
2
2
2
6
2
4
R
R
R
S
p
p
p
=
+
=
圆柱全
Q
4.若两球体积之比是1:2,则其表面积之比是______.
练习一
1.若球的表面积变为原来的2倍,则半径变为原来的___倍.
2.若球半径变为原来的2倍,则表面积变为原来的___倍.
3.若两球表面积之比为1:2,则其体积之比是______.
课堂练习
6.将半径为1和2的两个铅球,熔成一个大铅球,那么
这个大铅球的表面积是______.
5.若两球表面积之差为48π ,它们大圆周长之和为12π ,
则两球的直径之差为______.
练习二
课堂练习
例3.钢球直径是5cm,求它的体积和表面积.
(变式1)一种空心钢球的质量是142g,外径是5cm,求它的内径.(钢的密度是7.9g/cm2)
解:设空心钢球的内径为2xcm,则钢球的质量是
答:空心钢球的内径约为4.5cm.
“内径”是指内壁的直径,“外径”是指外壁直径。
(变式2)把直径为5cm钢球放入一个正方体的有盖纸盒中,至少要用多少纸
解:当球内切于正方体时用料最省时
此时棱长=直径=5cm
答:至少要用纸150cm2
两个几何体相切:一个几何体的各个面与另一个几何体的各面相切.
分析:用料最省时,球与正方体有什么位置关系
球内切于正方体
例4.如图,正方体的棱长为a,它的各个顶点都在球的球面上,求球的表面积和体积。
分析:正方体内接于球,则由球和正方体都是中心对称图形可知,它们中心重合,则正方体对角线与球的直径相等。
两个几何体相接:一个几何体的所有顶点都 在另一个几何体的表面上。
(变式) 球的内接长方体的长、宽、高分别为3、2、 ,求此球体的表面积和体积。
分析:长方体内接于球,则由球和长方体都是中心对称图形可知,它们中心重合,则长方体对角线与球的直径相等。
例5、如图是一个奖杯的三视图,单位是cm,
试画出它的直观图,并计算这个奖杯的体积.
(精确到0.01cm)
8
6
6
18
5
15
15
11
11
x/
y/
z/
解:这个奖杯的体积为
V=V正四棱台+V长方体+ V球
其中
V正四棱台
V长方体=6×8×18=864
V球=
所以这个奖杯的体积为
V ≈ 1828.76(cm3)
小结:
(1)有关球和球面的概念。
(2)球的体积公式:
球的表面积公式:
(3)球的体积公式和表面积的一些运用。
(4)多面体的“切”、“接”问题,必须明确“切”、“接”位置和有关元素间的数量关系,常借助“截面”图形来解决。
