2022年春人教版八年级数学下册19.1.1变量与函数练习(word解析版)
文档属性
| 名称 | 2022年春人教版八年级数学下册19.1.1变量与函数练习(word解析版) |
|
|
| 格式 | zip | ||
| 文件大小 | 105.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-24 21:17:58 | ||
图片预览

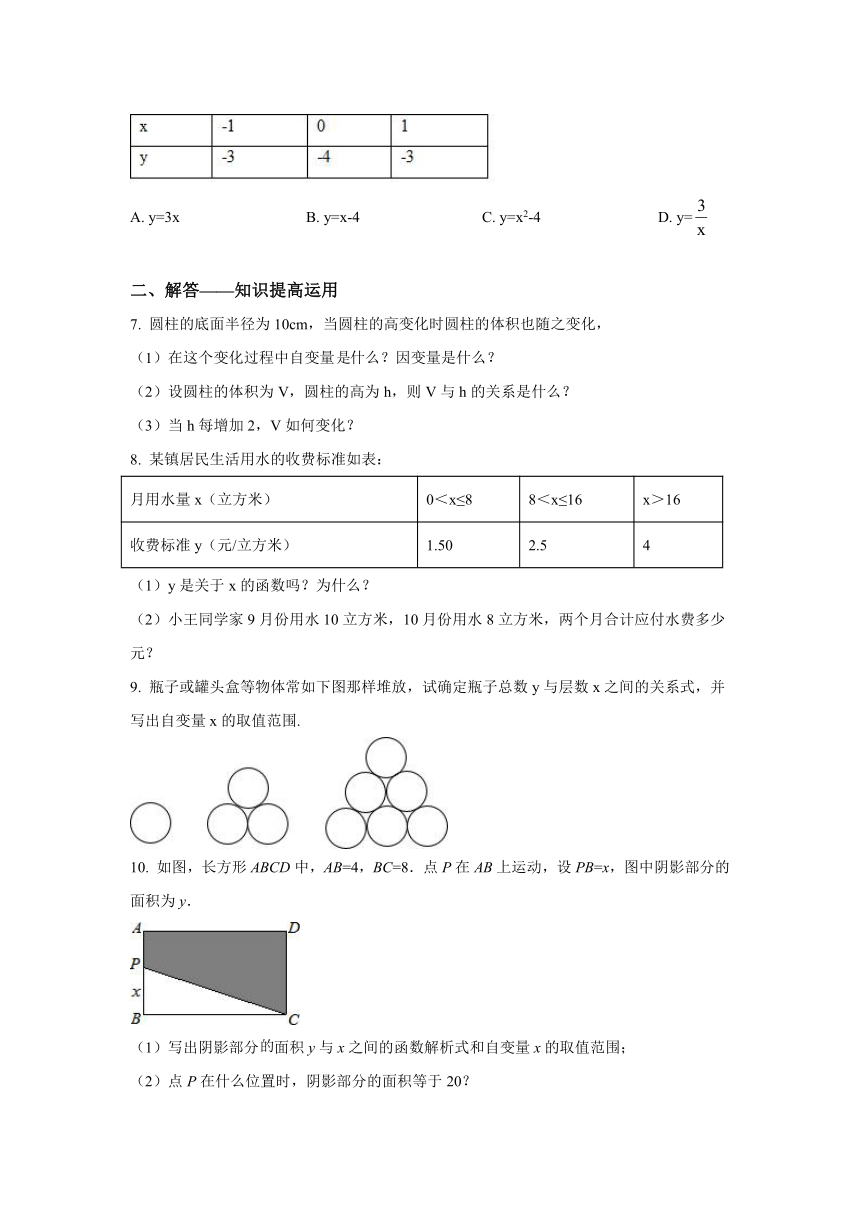



文档简介
《变量与函数》练习
一、选择——基础知识运用
1. 下列四个关系式:(1)y=x;(2)y=x2;(3)y=x3;(4)|y|=x,其中y不是x的函数的是( )
A. (1) B. (2) C. (3) D. (4)
2. 如果每盒钢笔有10支,售价25元,那么购买钢笔的总钱数y(元)与支数x之间的关系式为( )
A. y=10x B. y=25x C. y= x D. y= x
3. 如图,y是x的函数图像的是( )
A. B.
C. D.
4. 下列说法正确的是( )
A. 变量x、y满足y2=x,则y是x的函数
B. 变量x、y满足x+3y=1,则y是x函数
C. 代数式πr3是它所含字母r的函数
D. 在V=πr3中,是常量,r是自变量,V是r的函数
5. 已知x=3﹣k,y=2+k,则y与x的关系是( )
A. y=x﹣5 B. x+y=1 C. x﹣y=1 D. x+y=5
6. 已知两个变量x和y,它们之间3组对应值如下表,则y与x之间的函数关系式可能是( )
A. y=3x B. y=x-4 C. y=x2-4 D. y=
二、解答——知识提高运用
7. 圆柱的底面半径为10cm,当圆柱的高变化时圆柱的体积也随之变化,
(1)在这个变化过程中自变量什么?因变量是什么?
(2)设圆柱的体积为V,圆柱的高为h,则V与h的关系是什么?
(3)当h每增加2,V如何变化?
8. 某镇居民生活用水的收费标准如表:
月用水量x(立方米) 0<x≤8 8<x≤16 x>16
收费标准y(元/立方米) 1.50 2.5 4
(1)y是关于x的函数吗?为什么?
(2)小王同学家9月份用水10立方米,10月份用水8立方米,两个月合计应付水费多少元?
9. 瓶子或罐头盒等物体常如下图那样堆放,试确定瓶子总数y与层数x之间的关系式,并写出自变量x的取值范围.
10. 如图,长方形ABCD中,AB=4,BC=8.点P在AB上运动,设PB=x,图中阴影部分的面积为y.
(1)写出阴影部分面积y与x之间的函数解析式和自变量x的取值范围;
(2)点P在什么位置时,阴影部分的面积等于20?
11. 用一根长是20cm的细绳围成一个长方形(如图),这个长方形的一边的长为xcm,它的面积为ycm2.
(1)写出y与x之间的关系式,在这个关系式中,哪个是自变量 它的取值应在什么范围内
(2)用表格表示当x从1变到9时(每次增加1),y的相应值;
(3)从上面的表格中,你能看出什么规律
(4)猜想一下,怎样围法,得到的长方形的面积最大 最大是多少
(5)估计一下,当围成的长方形的面积是22cm2时,x的值应介于哪两个相邻整数之间
12. 直角三角形ABC中,∠ABC=90°,AC=10,BC=6,AB=8.P是AC上的一个动点,当P在AC上运动时,设PC=x,△ABP的面积为y.
(1)求y与x之间的关系式;
(2)点P在什么位置时,△ABP的面积等于△ABC的面积的.
《变量与函数》练习(解析版)
一、选择——基础知识运用
1. 下列四个关系式:(1)y=x;(2)y=x2;(3)y=x3;(4)|y|=x,其中y不是x的函数的是( )
A. (1) B. (2) C. (3) D. (4)
【1题答案】
【答案】D
【解析】
【详解】根据对于x的每一个取值,y都有唯一确定的值与之对应,(1)y=x,(2)y=x2,(3)y=x3满足函数的定义,y是x的函数,(4)|y|=x,当x取值时,y不是有唯一的值对应,y不是x的函数,故选D.
2. 如果每盒钢笔有10支,售价25元,那么购买钢笔的总钱数y(元)与支数x之间的关系式为( )
A. y=10x B. y=25x C. y= x D. y= x
【2题答案】
【答案】D
【解析】
【详解】解:一只钢笔的售价为:25÷10= (元),
所以购买钢笔的总钱数y(元)与支数x之间的关系式为:y= x.
故选D.
3. 如图,y是x的函数图像的是( )
A. B.
C. D.
【3题答案】
【答案】C
【解析】
【详解】对于x的每一个取值,y都有唯一确定的值,则y就是x的函数,选项A、B、D的图象上两个或三个点的横坐标相同,也就是说对于x的每一个取值,y的值不唯一,只有选项C符合函数的定义,故选C.
4. 下列说法正确的是( )
A. 变量x、y满足y2=x,则y是x的函数
B. 变量x、y满足x+3y=1,则y是x的函数
C. 代数式πr3是它所含字母r的函数
D. 在V=πr3中,是常量,r是自变量,V是r的函数
【4题答案】
【答案】B
【解析】
【详解】选项A,y与x不是唯一的值对应,选项A错误;选项B,当x取一值时,y有唯一的值与之对应,选项B正确;选项C、代数式,选项C错误;选项D,在V=πr3中,π是常量,r是自变量,V是r的函数,选项D错误.故选B.
5. 已知x=3﹣k,y=2+k,则y与x的关系是( )
A. y=x﹣5 B. x+y=1 C. x﹣y=1 D. x+y=5
【5题答案】
【答案】D
【解析】
【详解】∵x=3﹣k,y=2+k,
∴x+y=3﹣k+2+k=5.
故选D.
6. 已知两个变量x和y,它们之间的3组对应值如下表,则y与x之间的函数关系式可能是( )
A. y=3x B. y=x-4 C. y=x2-4 D. y=
【6题答案】
【答案】C
【解析】
【详解】选项A,y=3x,根据表格对应数据代入得出y≠3x,选项A错误;选项B,y=x-4,根据表格对应数据代入得出y≠x-4,选项B错误;选项C,y=x2-4,根据表格对应数据代入得出y=x2-4,选项C正确;选项D,y= ,根据表格对应数据代入得出y≠,选项D错误.故选C.
二、解答——知识提高运用
7. 圆柱的底面半径为10cm,当圆柱的高变化时圆柱的体积也随之变化,
(1)在这个变化过程中自变量是什么?因变量是什么?
(2)设圆柱的体积为V,圆柱的高为h,则V与h的关系是什么?
(3)当h每增加2,V如何变化?
【7题答案】
【答案】(1)自变量是圆柱高h,因变量是圆柱的体积V;
(2)圆柱的体积V与圆柱的高的关系式是:V=100πh;
(3)当h每增加2时,V增加200πcm3.
【解析】
【详解】试题分析:(1)由圆柱的高变化时圆柱的体积也随之变化,即可得结论;(2)根据圆柱的体积公式即可得V与h的关系式;(3)分别计算出高为h和高为h+2时圆柱的体积,比较即可.
试题解析:
(1)由于圆柱的高变化时圆柱的体积也随之变化,所以自变量是圆柱的高h,因变量是圆柱的体积V;
(2)圆柱的体积V与圆柱的高的关系式是:V=100πh;
(3)由于V=100π(h+2)=100πh+200π;所以当h每增加2时,V增加200πcm3.
点睛:本题考查了函数关系式、函数值及变量的知识,属于基础题,注意课本基础知识的掌握.
8. 某镇居民生活用水的收费标准如表:
月用水量x(立方米) 0<x≤8 8<x≤16 x>16
收费标准y(元/立方米) 1.50 2.5 4
(1)y是关于x的函数吗?为什么?
(2)小王同学家9月份用水10立方米,10月份用水8立方米,两个月合计应付水费多少元?
【8题答案】
【答案】(1)y是关于x的函数,理由见解析;(2)两个月合计应付水费29元.
【解析】
【详解】试题分析:(1)观察图表可得,存在有两个变量(用水量x和收费标准y),对于x每取一个值,都有唯一确定的y值与之相对应,根据函数的定义即可得结论;(2)根据表格中所给的数据分别计算九、十月份的水费,再求和即可.
试题解析:
(1)存在两个变量:用水量x和收费标准y(单价),对于x每取一个值,都有唯一确定的y值与之相对应,符合函数的定义,
∴y是关于x的函数.
(2)1.5×8+(10-8)×2.5+1.5×8=29(元).
答:两个月合计应付水费29元.
9. 瓶子或罐头盒等物体常如下图那样堆放,试确定瓶子总数y与层数x之间的关系式,并写出自变量x的取值范围.
【9题答案】
【答案】y=(x≥1)
【解析】
【详解】试题分析:根据所给的图形可得:当n为1时,y=1;当n=2时,y=1+2;当n=3时,y=1+2+3,···,y=1+2+3+…+n,即可得y与x的函数关系式.
试题解析:
填表如下:
x 1 2 3 4 …
y 1 3 6 10 …
依题意得:y=1+2+3+…+x= (x≥1的整数).
10. 如图,长方形ABCD中,AB=4,BC=8.点P在AB上运动,设PB=x,图中阴影部分的面积为y.
(1)写出阴影部分的面积y与x之间的函数解析式和自变量x的取值范围;
(2)点P在什么位置时,阴影部分的面积等于20?
【10题答案】
【答案】(1)阴影部分的面积为:y=32-4x(0<x≤4);(2)PB=3
【解析】
【分析】(1)根据梯形的面积公式得出y与x的函数关系式即可;
(2)利用(1)中所求得出y=20,求出x即可得出答案.
【详解】解:(1)设PB=x,长方形ABCD中,AB=4,BC=8,
则图中阴影部分的面积为:y=(4-x+4)×8=32-4x(0≤x≤4).
(2)当y=20时,20=32-4x,
解得x=3,
即PB=3.
11. 用一根长是20cm的细绳围成一个长方形(如图),这个长方形的一边的长为xcm,它的面积为ycm2.
(1)写出y与x之间的关系式,在这个关系式中,哪个是自变量 它的取值应在什么范围内
(2)用表格表示当x从1变到9时(每次增加1),y的相应值;
(3)从上面表格中,你能看出什么规律
(4)猜想一下,怎样围法,得到长方形的面积最大 最大是多少
(5)估计一下,当围成的长方形的面积是22cm2时,x的值应介于哪两个相邻整数之间
【11题答案】
【答案】(1)y=·x=(10-x)·x,x是自变量,它的值应在0到10之间(不包括0和10)
(2)
x
1
2
3
4
5
6
7
8
9
10
y
9
16
21
24
25
24
21
16
9
(3)可以看出:①当x逐渐增大时,y的值先由小变大,后又由大变小;②y的值在由小变大的过程中,变大的速度越来越慢,反过来y的值在由大变小的过程中,变小的速度越来越快;③当x取距5等距离的两数时,得到的两个y值相等.
(4)从表中可以发现x=5时,y取到最大的值25.
(5)根据表格:当x=22时,x应介于3和4之间或者6与7之间.
【解析】
【详解】试题分析:(1)根据长方形的面积公式即可得到结果,再根据常量的定义来判断自变量及其范围;
(2)分别把x=1变到9的值代入,即可得到结果;
(3)认真分析表中数据的特征即可得到结果;
(4)认真分析表中数据的特征即可得到结果;
(5)认真分析表中数据的特征即可得到结果.
(1)y=·x=(10-x)·x,x是自变量,它的值应在0到10之间(不包括0和10)
(2)
x
1
2
3
4
5
6
7
8
9
10
y
9
16
21
24
25
24
21
16
9
(3)可以看出:①当x逐渐增大时,y的值先由小变大,后又由大变小;②y的值在由小变大的过程中,变大的速度越来越慢,反过来y的值在由大变小的过程中,变小的速度越来越快;③当x取距5等距离的两数时,得到的两个y值相等.
(4)从表中可以发现x=5时,y取到最大的值25.
(5)根据表格:当x=22时,x应介于3和4之间或者6与7之间.
考点:本题主要考查变量的定义,长方形的面积公式
点评:解答本题的关键是熟练掌握长方形的面积公式,同时熟记在一个变化的过程中,数值发生变化的量称为变量,函数值为因变量,另一个值为自变量.
12. 直角三角形ABC中,∠ABC=90°,AC=10,BC=6,AB=8.P是AC上的一个动点,当P在AC上运动时,设PC=x,△ABP的面积为y.
(1)求y与x之间关系式;
(2)点P在什么位置时,△ABP的面积等于△ABC的面积的.
【12题答案】
【答案】(1)y与x之间的关系式为:y=-x+24;(2)点P在距点C处.
【解析】
【详解】试题分析:(1)如图,作PD⊥AB,可得△ADP∽△ABC,根据相似三角形的性质,可用x表示出PD的长,根据S△ABP=AB×PD,代入数值,即可求出y与x之间的关系式.(2)根据题意,△ABP的面积等于△ABC的面积的,则S△ABP=AB×PD=××6×8,即可得出x的值,可确定点P的位置;
试题解析:
(1)如图,作PD⊥AB,
∴△ADP∽△ABC,
∴ = ,即 = ,
解得,PD= ,
∴S△ABP= AB×PD=×8× = -x+24,
∴y与x之间关系式为:y=-x+24;
(2)由题意,S△ABC= ×6×8=24,
∵△ABP的面积等于△ABC的面积的,
∴S△ABP=S△ABC=×24=8,
即-x+24=8,
解得,x=,
∴点P在距点C处.
点睛:本题考查了相似三角形的判定及性质、一次函数的应用等知识点,利用相似三角形的性质求得y与x之间的关系式是解题的关键.
一、选择——基础知识运用
1. 下列四个关系式:(1)y=x;(2)y=x2;(3)y=x3;(4)|y|=x,其中y不是x的函数的是( )
A. (1) B. (2) C. (3) D. (4)
2. 如果每盒钢笔有10支,售价25元,那么购买钢笔的总钱数y(元)与支数x之间的关系式为( )
A. y=10x B. y=25x C. y= x D. y= x
3. 如图,y是x的函数图像的是( )
A. B.
C. D.
4. 下列说法正确的是( )
A. 变量x、y满足y2=x,则y是x的函数
B. 变量x、y满足x+3y=1,则y是x函数
C. 代数式πr3是它所含字母r的函数
D. 在V=πr3中,是常量,r是自变量,V是r的函数
5. 已知x=3﹣k,y=2+k,则y与x的关系是( )
A. y=x﹣5 B. x+y=1 C. x﹣y=1 D. x+y=5
6. 已知两个变量x和y,它们之间3组对应值如下表,则y与x之间的函数关系式可能是( )
A. y=3x B. y=x-4 C. y=x2-4 D. y=
二、解答——知识提高运用
7. 圆柱的底面半径为10cm,当圆柱的高变化时圆柱的体积也随之变化,
(1)在这个变化过程中自变量什么?因变量是什么?
(2)设圆柱的体积为V,圆柱的高为h,则V与h的关系是什么?
(3)当h每增加2,V如何变化?
8. 某镇居民生活用水的收费标准如表:
月用水量x(立方米) 0<x≤8 8<x≤16 x>16
收费标准y(元/立方米) 1.50 2.5 4
(1)y是关于x的函数吗?为什么?
(2)小王同学家9月份用水10立方米,10月份用水8立方米,两个月合计应付水费多少元?
9. 瓶子或罐头盒等物体常如下图那样堆放,试确定瓶子总数y与层数x之间的关系式,并写出自变量x的取值范围.
10. 如图,长方形ABCD中,AB=4,BC=8.点P在AB上运动,设PB=x,图中阴影部分的面积为y.
(1)写出阴影部分面积y与x之间的函数解析式和自变量x的取值范围;
(2)点P在什么位置时,阴影部分的面积等于20?
11. 用一根长是20cm的细绳围成一个长方形(如图),这个长方形的一边的长为xcm,它的面积为ycm2.
(1)写出y与x之间的关系式,在这个关系式中,哪个是自变量 它的取值应在什么范围内
(2)用表格表示当x从1变到9时(每次增加1),y的相应值;
(3)从上面的表格中,你能看出什么规律
(4)猜想一下,怎样围法,得到的长方形的面积最大 最大是多少
(5)估计一下,当围成的长方形的面积是22cm2时,x的值应介于哪两个相邻整数之间
12. 直角三角形ABC中,∠ABC=90°,AC=10,BC=6,AB=8.P是AC上的一个动点,当P在AC上运动时,设PC=x,△ABP的面积为y.
(1)求y与x之间的关系式;
(2)点P在什么位置时,△ABP的面积等于△ABC的面积的.
《变量与函数》练习(解析版)
一、选择——基础知识运用
1. 下列四个关系式:(1)y=x;(2)y=x2;(3)y=x3;(4)|y|=x,其中y不是x的函数的是( )
A. (1) B. (2) C. (3) D. (4)
【1题答案】
【答案】D
【解析】
【详解】根据对于x的每一个取值,y都有唯一确定的值与之对应,(1)y=x,(2)y=x2,(3)y=x3满足函数的定义,y是x的函数,(4)|y|=x,当x取值时,y不是有唯一的值对应,y不是x的函数,故选D.
2. 如果每盒钢笔有10支,售价25元,那么购买钢笔的总钱数y(元)与支数x之间的关系式为( )
A. y=10x B. y=25x C. y= x D. y= x
【2题答案】
【答案】D
【解析】
【详解】解:一只钢笔的售价为:25÷10= (元),
所以购买钢笔的总钱数y(元)与支数x之间的关系式为:y= x.
故选D.
3. 如图,y是x的函数图像的是( )
A. B.
C. D.
【3题答案】
【答案】C
【解析】
【详解】对于x的每一个取值,y都有唯一确定的值,则y就是x的函数,选项A、B、D的图象上两个或三个点的横坐标相同,也就是说对于x的每一个取值,y的值不唯一,只有选项C符合函数的定义,故选C.
4. 下列说法正确的是( )
A. 变量x、y满足y2=x,则y是x的函数
B. 变量x、y满足x+3y=1,则y是x的函数
C. 代数式πr3是它所含字母r的函数
D. 在V=πr3中,是常量,r是自变量,V是r的函数
【4题答案】
【答案】B
【解析】
【详解】选项A,y与x不是唯一的值对应,选项A错误;选项B,当x取一值时,y有唯一的值与之对应,选项B正确;选项C、代数式,选项C错误;选项D,在V=πr3中,π是常量,r是自变量,V是r的函数,选项D错误.故选B.
5. 已知x=3﹣k,y=2+k,则y与x的关系是( )
A. y=x﹣5 B. x+y=1 C. x﹣y=1 D. x+y=5
【5题答案】
【答案】D
【解析】
【详解】∵x=3﹣k,y=2+k,
∴x+y=3﹣k+2+k=5.
故选D.
6. 已知两个变量x和y,它们之间的3组对应值如下表,则y与x之间的函数关系式可能是( )
A. y=3x B. y=x-4 C. y=x2-4 D. y=
【6题答案】
【答案】C
【解析】
【详解】选项A,y=3x,根据表格对应数据代入得出y≠3x,选项A错误;选项B,y=x-4,根据表格对应数据代入得出y≠x-4,选项B错误;选项C,y=x2-4,根据表格对应数据代入得出y=x2-4,选项C正确;选项D,y= ,根据表格对应数据代入得出y≠,选项D错误.故选C.
二、解答——知识提高运用
7. 圆柱的底面半径为10cm,当圆柱的高变化时圆柱的体积也随之变化,
(1)在这个变化过程中自变量是什么?因变量是什么?
(2)设圆柱的体积为V,圆柱的高为h,则V与h的关系是什么?
(3)当h每增加2,V如何变化?
【7题答案】
【答案】(1)自变量是圆柱高h,因变量是圆柱的体积V;
(2)圆柱的体积V与圆柱的高的关系式是:V=100πh;
(3)当h每增加2时,V增加200πcm3.
【解析】
【详解】试题分析:(1)由圆柱的高变化时圆柱的体积也随之变化,即可得结论;(2)根据圆柱的体积公式即可得V与h的关系式;(3)分别计算出高为h和高为h+2时圆柱的体积,比较即可.
试题解析:
(1)由于圆柱的高变化时圆柱的体积也随之变化,所以自变量是圆柱的高h,因变量是圆柱的体积V;
(2)圆柱的体积V与圆柱的高的关系式是:V=100πh;
(3)由于V=100π(h+2)=100πh+200π;所以当h每增加2时,V增加200πcm3.
点睛:本题考查了函数关系式、函数值及变量的知识,属于基础题,注意课本基础知识的掌握.
8. 某镇居民生活用水的收费标准如表:
月用水量x(立方米) 0<x≤8 8<x≤16 x>16
收费标准y(元/立方米) 1.50 2.5 4
(1)y是关于x的函数吗?为什么?
(2)小王同学家9月份用水10立方米,10月份用水8立方米,两个月合计应付水费多少元?
【8题答案】
【答案】(1)y是关于x的函数,理由见解析;(2)两个月合计应付水费29元.
【解析】
【详解】试题分析:(1)观察图表可得,存在有两个变量(用水量x和收费标准y),对于x每取一个值,都有唯一确定的y值与之相对应,根据函数的定义即可得结论;(2)根据表格中所给的数据分别计算九、十月份的水费,再求和即可.
试题解析:
(1)存在两个变量:用水量x和收费标准y(单价),对于x每取一个值,都有唯一确定的y值与之相对应,符合函数的定义,
∴y是关于x的函数.
(2)1.5×8+(10-8)×2.5+1.5×8=29(元).
答:两个月合计应付水费29元.
9. 瓶子或罐头盒等物体常如下图那样堆放,试确定瓶子总数y与层数x之间的关系式,并写出自变量x的取值范围.
【9题答案】
【答案】y=(x≥1)
【解析】
【详解】试题分析:根据所给的图形可得:当n为1时,y=1;当n=2时,y=1+2;当n=3时,y=1+2+3,···,y=1+2+3+…+n,即可得y与x的函数关系式.
试题解析:
填表如下:
x 1 2 3 4 …
y 1 3 6 10 …
依题意得:y=1+2+3+…+x= (x≥1的整数).
10. 如图,长方形ABCD中,AB=4,BC=8.点P在AB上运动,设PB=x,图中阴影部分的面积为y.
(1)写出阴影部分的面积y与x之间的函数解析式和自变量x的取值范围;
(2)点P在什么位置时,阴影部分的面积等于20?
【10题答案】
【答案】(1)阴影部分的面积为:y=32-4x(0<x≤4);(2)PB=3
【解析】
【分析】(1)根据梯形的面积公式得出y与x的函数关系式即可;
(2)利用(1)中所求得出y=20,求出x即可得出答案.
【详解】解:(1)设PB=x,长方形ABCD中,AB=4,BC=8,
则图中阴影部分的面积为:y=(4-x+4)×8=32-4x(0≤x≤4).
(2)当y=20时,20=32-4x,
解得x=3,
即PB=3.
11. 用一根长是20cm的细绳围成一个长方形(如图),这个长方形的一边的长为xcm,它的面积为ycm2.
(1)写出y与x之间的关系式,在这个关系式中,哪个是自变量 它的取值应在什么范围内
(2)用表格表示当x从1变到9时(每次增加1),y的相应值;
(3)从上面表格中,你能看出什么规律
(4)猜想一下,怎样围法,得到长方形的面积最大 最大是多少
(5)估计一下,当围成的长方形的面积是22cm2时,x的值应介于哪两个相邻整数之间
【11题答案】
【答案】(1)y=·x=(10-x)·x,x是自变量,它的值应在0到10之间(不包括0和10)
(2)
x
1
2
3
4
5
6
7
8
9
10
y
9
16
21
24
25
24
21
16
9
(3)可以看出:①当x逐渐增大时,y的值先由小变大,后又由大变小;②y的值在由小变大的过程中,变大的速度越来越慢,反过来y的值在由大变小的过程中,变小的速度越来越快;③当x取距5等距离的两数时,得到的两个y值相等.
(4)从表中可以发现x=5时,y取到最大的值25.
(5)根据表格:当x=22时,x应介于3和4之间或者6与7之间.
【解析】
【详解】试题分析:(1)根据长方形的面积公式即可得到结果,再根据常量的定义来判断自变量及其范围;
(2)分别把x=1变到9的值代入,即可得到结果;
(3)认真分析表中数据的特征即可得到结果;
(4)认真分析表中数据的特征即可得到结果;
(5)认真分析表中数据的特征即可得到结果.
(1)y=·x=(10-x)·x,x是自变量,它的值应在0到10之间(不包括0和10)
(2)
x
1
2
3
4
5
6
7
8
9
10
y
9
16
21
24
25
24
21
16
9
(3)可以看出:①当x逐渐增大时,y的值先由小变大,后又由大变小;②y的值在由小变大的过程中,变大的速度越来越慢,反过来y的值在由大变小的过程中,变小的速度越来越快;③当x取距5等距离的两数时,得到的两个y值相等.
(4)从表中可以发现x=5时,y取到最大的值25.
(5)根据表格:当x=22时,x应介于3和4之间或者6与7之间.
考点:本题主要考查变量的定义,长方形的面积公式
点评:解答本题的关键是熟练掌握长方形的面积公式,同时熟记在一个变化的过程中,数值发生变化的量称为变量,函数值为因变量,另一个值为自变量.
12. 直角三角形ABC中,∠ABC=90°,AC=10,BC=6,AB=8.P是AC上的一个动点,当P在AC上运动时,设PC=x,△ABP的面积为y.
(1)求y与x之间关系式;
(2)点P在什么位置时,△ABP的面积等于△ABC的面积的.
【12题答案】
【答案】(1)y与x之间的关系式为:y=-x+24;(2)点P在距点C处.
【解析】
【详解】试题分析:(1)如图,作PD⊥AB,可得△ADP∽△ABC,根据相似三角形的性质,可用x表示出PD的长,根据S△ABP=AB×PD,代入数值,即可求出y与x之间的关系式.(2)根据题意,△ABP的面积等于△ABC的面积的,则S△ABP=AB×PD=××6×8,即可得出x的值,可确定点P的位置;
试题解析:
(1)如图,作PD⊥AB,
∴△ADP∽△ABC,
∴ = ,即 = ,
解得,PD= ,
∴S△ABP= AB×PD=×8× = -x+24,
∴y与x之间关系式为:y=-x+24;
(2)由题意,S△ABC= ×6×8=24,
∵△ABP的面积等于△ABC的面积的,
∴S△ABP=S△ABC=×24=8,
即-x+24=8,
解得,x=,
∴点P在距点C处.
点睛:本题考查了相似三角形的判定及性质、一次函数的应用等知识点,利用相似三角形的性质求得y与x之间的关系式是解题的关键.
