西南师大版五年级数学下册三 长方体 正方体《长方体和正方体的体积计算》 教案
文档属性
| 名称 | 西南师大版五年级数学下册三 长方体 正方体《长方体和正方体的体积计算》 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 290.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-24 08:57:31 | ||
图片预览


文档简介
《长方体与正方体的体积》教案
教学目标
1. 经历从实物中抽象出数学模型,探索影响长方体体积大小的因素。
2.观察操作,自主探索公式,能正确计算长方体、正方体的体积。
3.培养学生积极思考、探索新知的思维品质,发展学生的空间观念。
教学重点
理解、掌握、应用长方体和正方体体积公式.
教学难点
长方体和正方体体积公式的推导,学生空间观念的培养。
教学过程
一、长方体“三视图”的剖析,建立表象
1、复习准备.
师:这节课以前已经学习了哪些体积单位 你对这些体积单位有什么认识?
2、导入
①出示 ,把不规则图形变成长方体。
师:棱长1厘米的正方体体积是1立方厘米,下面(图1)物体的体积是多少?
图1 图2
师:你有什么好办法,使我们一目了然体积是6立方厘米?(动画演示移动一个小正方体由图1变成图2)
师:下面的图形(图3)你能移动一下把它也变成长方体吗?(动画演示移动一个小正方体由图3变成图4)
图3 图4
② 图2与图4两个长方体有什么联系?(同一个长方体,摆放的位置不同)
③ 引导学生说出第三种观察角度的长方体
图5
④小结:同一个长方体,由于观察的角度不同,它的长、宽、高会相互转化,但大小不变。
【设计意图】通过不规则图形与长方体之间的转化,得出长方体比不规则图形更容易数清它体积的结论,更重要的是让学生通过想象得出了第3种观察角度的图形,从三个不同角度观察长方体,丰富学生对于长方体的表象积累,培养学生的空间想象力。
二、建立实物与数学模型之间的联系
1.(出示图6)下面这个复杂的图形如果摆成长方体,会是怎样的?体积又是多少?
图6 图7
2.师演示出图7中抽离出来的图8,这个长方体的体积是多少?为什么?
图8
3.师演示拉伸长方体的高,形成图9,现在长方体的体积是多少
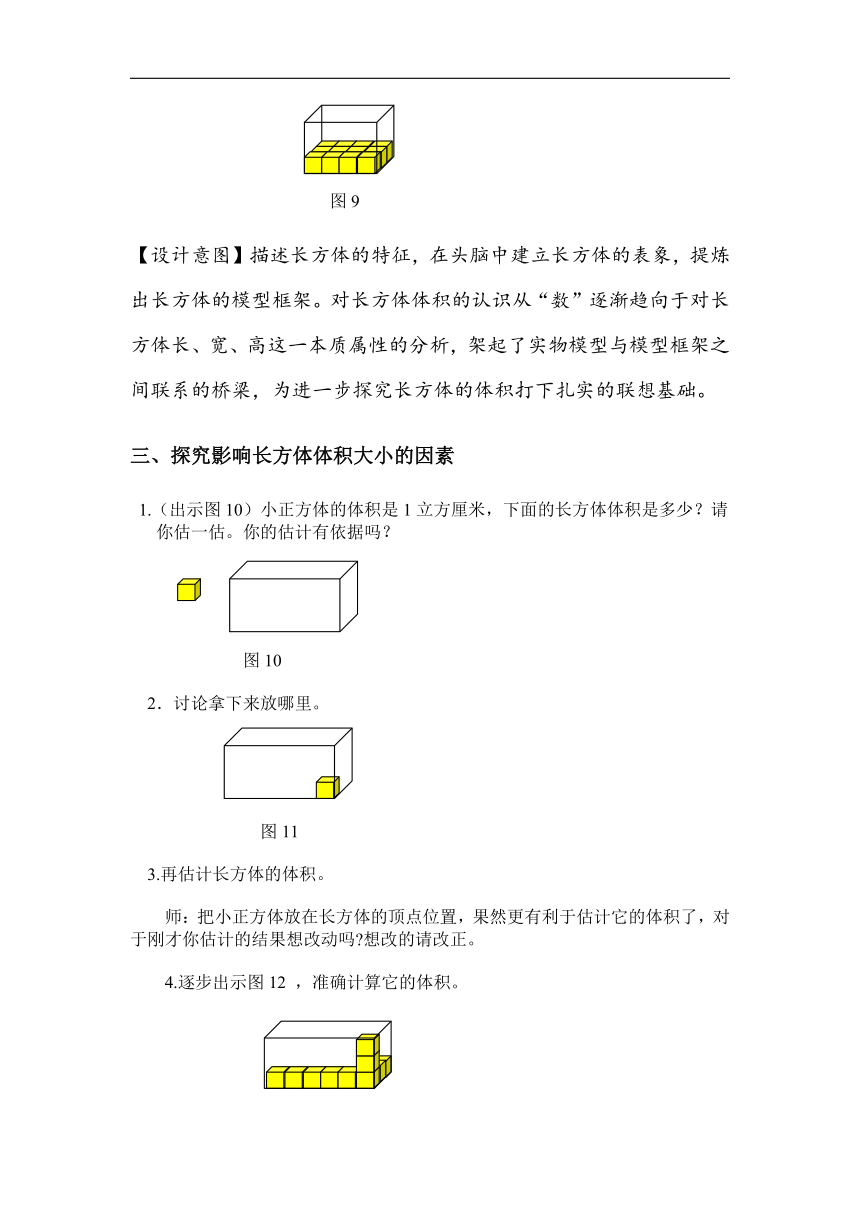
图9
【设计意图】描述长方体的特征,在头脑中建立长方体的表象,提炼出长方体的模型框架。对长方体体积的认识从“数”逐渐趋向于对长方体长、宽、高这一本质属性的分析,架起了实物模型与模型框架之间联系的桥梁,为进一步探究长方体的体积打下扎实的联想基础。
三、探究影响长方体体积大小的因素
1.(出示图10)小正方体的体积是1立方厘米,下面的长方体体积是多少?请你估一估。你的估计有依据吗?
图10
2.讨论拿下来放哪里。
图11
3.再估计长方体的体积。
师:把小正方体放在长方体的顶点位置,果然更有利于估计它的体积了,对于刚才你估计的结果想改动吗 想改的请改正。
4.逐步出示图12 ,准确计算它的体积。
图12
5.计算下面长方体的体积(图13)
3厘米
9厘米
【设计意图】本环节设计从长方体的形成入手,反其道而行,先有长方体的框架,在描述如何摆。在估算长方体体积的过程中理顺关系、确定估算方法,逐渐逼近准确答案,直指影响长方体体积大小的本质属性—长、宽、高。
四、概括长方体体积计算公式
1.讨论
师:通过刚才的研究,我们发现长方体的体积和什么有关系?(长、宽、高)
2.师出示一个长方体,分别拉伸它的长、宽、高。观察体积的变化;把图形旋转观察体积的变化。
师:把图形旋转和你能找到这个图形的长、宽、高吗?
师:如果这个长方体的长是a 厘米,宽是b 厘米,高是h厘米,谁会求这个长方体的体积。
3.总结长方体的体积公式
教师板书:长方体的体积=长×宽×高
教师:用V表示体积,a表示长,b表示宽,h表示高,公式可以写成:
板书: V=a×b×h.
【设计意图】通过观察长、宽、高依次变化而引起体积变化的过程,进一步明确影响长方体体积大小的因素,自然概括体积公式。
五、练习中归纳正方体体积公式,统一长方体和正方体的体积公式
1.练习(规范书写格式,总结正方体体积公式)
5 12
2
2.归纳正方体的体积公式
教师板书:正方体体积=棱长×棱长×棱长.
用V表体积,a表示棱长
V=a×a×a或者V=a
3.统一长方体和正方体的体积计算公式
师:观察黑板上的体积计算公式,“a×b”在这里求的是什么?(长方体的底面积)。
师:如果知道长方体的底面积和高可以求它的体积吗?(前后桌讨论)
师:其实这种方法刚才同学们已经用过了,底面积可以表示下面一层的小正方体个数。
课件出示:
长方体的体积=底面积×高
师:正方体的体积可以用“底面积×高”来计算吗?
师:谁能用字母表示这个统一的体积公式呢?
板书: V=sh
六、运用模型,拓展提升
1、课本第51页例2:这个水果箱的体积是多少?
2、正方体的棱长如果扩大到原来的2倍,体积扩大到原来的多少倍?棱长如果扩大到原来的10倍呢?
2厘米
9厘米
教学目标
1. 经历从实物中抽象出数学模型,探索影响长方体体积大小的因素。
2.观察操作,自主探索公式,能正确计算长方体、正方体的体积。
3.培养学生积极思考、探索新知的思维品质,发展学生的空间观念。
教学重点
理解、掌握、应用长方体和正方体体积公式.
教学难点
长方体和正方体体积公式的推导,学生空间观念的培养。
教学过程
一、长方体“三视图”的剖析,建立表象
1、复习准备.
师:这节课以前已经学习了哪些体积单位 你对这些体积单位有什么认识?
2、导入
①出示 ,把不规则图形变成长方体。
师:棱长1厘米的正方体体积是1立方厘米,下面(图1)物体的体积是多少?
图1 图2
师:你有什么好办法,使我们一目了然体积是6立方厘米?(动画演示移动一个小正方体由图1变成图2)
师:下面的图形(图3)你能移动一下把它也变成长方体吗?(动画演示移动一个小正方体由图3变成图4)
图3 图4
② 图2与图4两个长方体有什么联系?(同一个长方体,摆放的位置不同)
③ 引导学生说出第三种观察角度的长方体
图5
④小结:同一个长方体,由于观察的角度不同,它的长、宽、高会相互转化,但大小不变。
【设计意图】通过不规则图形与长方体之间的转化,得出长方体比不规则图形更容易数清它体积的结论,更重要的是让学生通过想象得出了第3种观察角度的图形,从三个不同角度观察长方体,丰富学生对于长方体的表象积累,培养学生的空间想象力。
二、建立实物与数学模型之间的联系
1.(出示图6)下面这个复杂的图形如果摆成长方体,会是怎样的?体积又是多少?
图6 图7
2.师演示出图7中抽离出来的图8,这个长方体的体积是多少?为什么?
图8
3.师演示拉伸长方体的高,形成图9,现在长方体的体积是多少
图9
【设计意图】描述长方体的特征,在头脑中建立长方体的表象,提炼出长方体的模型框架。对长方体体积的认识从“数”逐渐趋向于对长方体长、宽、高这一本质属性的分析,架起了实物模型与模型框架之间联系的桥梁,为进一步探究长方体的体积打下扎实的联想基础。
三、探究影响长方体体积大小的因素
1.(出示图10)小正方体的体积是1立方厘米,下面的长方体体积是多少?请你估一估。你的估计有依据吗?
图10
2.讨论拿下来放哪里。
图11
3.再估计长方体的体积。
师:把小正方体放在长方体的顶点位置,果然更有利于估计它的体积了,对于刚才你估计的结果想改动吗 想改的请改正。
4.逐步出示图12 ,准确计算它的体积。
图12
5.计算下面长方体的体积(图13)
3厘米
9厘米
【设计意图】本环节设计从长方体的形成入手,反其道而行,先有长方体的框架,在描述如何摆。在估算长方体体积的过程中理顺关系、确定估算方法,逐渐逼近准确答案,直指影响长方体体积大小的本质属性—长、宽、高。
四、概括长方体体积计算公式
1.讨论
师:通过刚才的研究,我们发现长方体的体积和什么有关系?(长、宽、高)
2.师出示一个长方体,分别拉伸它的长、宽、高。观察体积的变化;把图形旋转观察体积的变化。
师:把图形旋转和你能找到这个图形的长、宽、高吗?
师:如果这个长方体的长是a 厘米,宽是b 厘米,高是h厘米,谁会求这个长方体的体积。
3.总结长方体的体积公式
教师板书:长方体的体积=长×宽×高
教师:用V表示体积,a表示长,b表示宽,h表示高,公式可以写成:
板书: V=a×b×h.
【设计意图】通过观察长、宽、高依次变化而引起体积变化的过程,进一步明确影响长方体体积大小的因素,自然概括体积公式。
五、练习中归纳正方体体积公式,统一长方体和正方体的体积公式
1.练习(规范书写格式,总结正方体体积公式)
5 12
2
2.归纳正方体的体积公式
教师板书:正方体体积=棱长×棱长×棱长.
用V表体积,a表示棱长
V=a×a×a或者V=a
3.统一长方体和正方体的体积计算公式
师:观察黑板上的体积计算公式,“a×b”在这里求的是什么?(长方体的底面积)。
师:如果知道长方体的底面积和高可以求它的体积吗?(前后桌讨论)
师:其实这种方法刚才同学们已经用过了,底面积可以表示下面一层的小正方体个数。
课件出示:
长方体的体积=底面积×高
师:正方体的体积可以用“底面积×高”来计算吗?
师:谁能用字母表示这个统一的体积公式呢?
板书: V=sh
六、运用模型,拓展提升
1、课本第51页例2:这个水果箱的体积是多少?
2、正方体的棱长如果扩大到原来的2倍,体积扩大到原来的多少倍?棱长如果扩大到原来的10倍呢?
2厘米
9厘米
