七年级数学下第一章复习

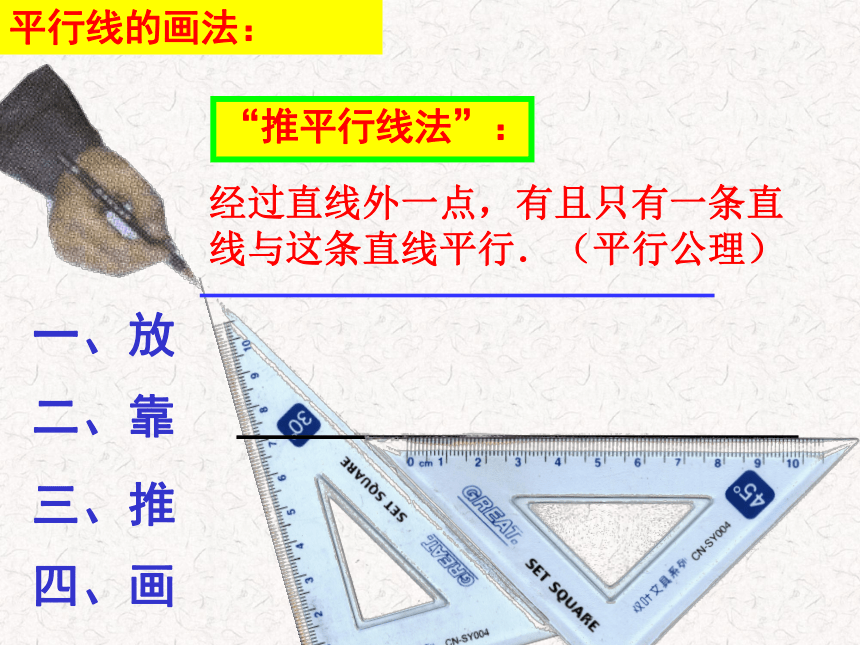
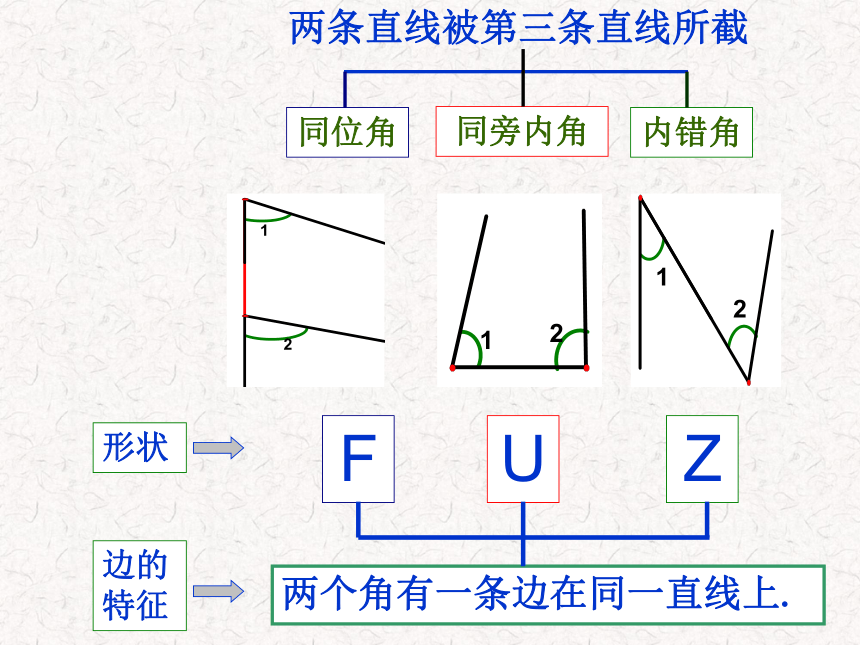
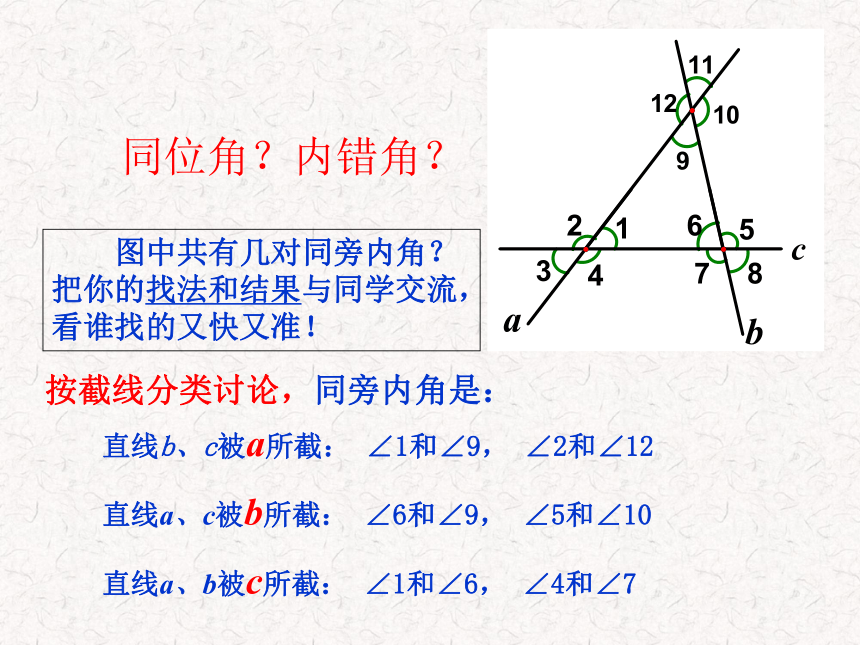
课件20张PPT。概念：1.平行线的定义：在同一平面内，不相交的两条直线叫做平行线。2.平行线的表示方法：平行用符号“∥”表示。如图，直线AB和CD是平行线，记作AB∥CD（或CD∥AB），读作“AB平行于CD”（或“CD平行于AB”）。若用m、n表示这两条直线，那么直线m与直线n平行，记作m∥n（或n∥m），读作“m平行于n”(或”n平行于m”)。一、放二、靠三、推四、画平行线的画法：“推平行线法”： 经过直线外一点，有且只有一条直线与这条直线平行．（平行公理）两条直线被第三条直线所截两个角有一条边在同一直线上.同位角同旁内角内错角形状边的特征FUZ 图中共有几对同旁内角？把你的找法和结果与同学交流，看谁找的又快又准！按截线分类讨论，同旁内角是：直线b、c被a所截： ∠1和∠9， ∠2和∠12
直线a、c被b所截： ∠6和∠9， ∠5和∠10
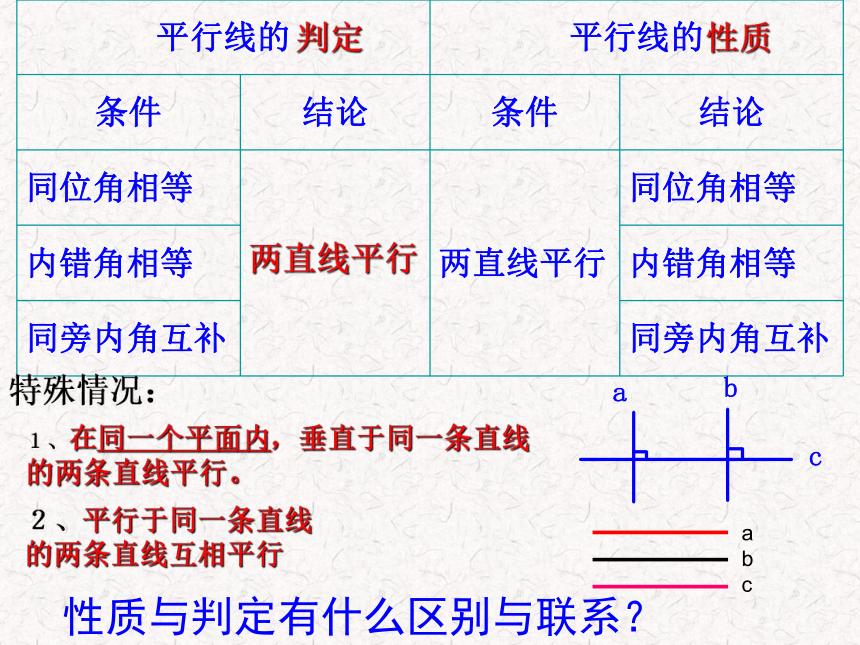
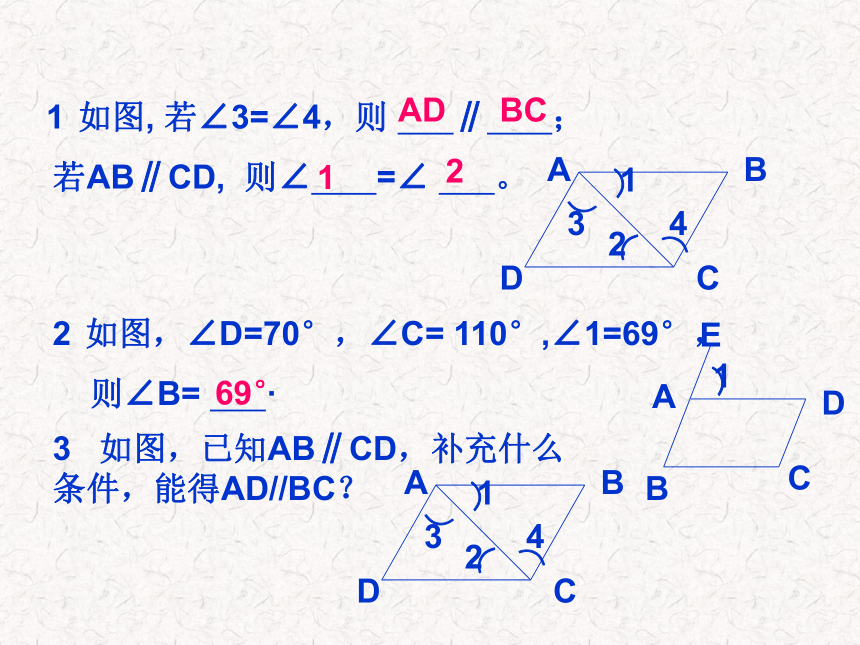
直线a、b被c所截： ∠1和∠6， ∠4和∠7同位角？内错角？性质与判定有什么区别与联系？判定性质两直线平行如图, 若∠3=∠4，则 ∥ ；AD1若AB∥CD, 则∠ =∠ 。
BC2如图，∠D=70°，∠C= 110°,∠1=69°，
则∠B= ·69°3 如图，已知AB∥CD，补充什么条件，能得AD//BC？5 若两条平行线被第三条直线所截，则一组内错角的平分线互相（ ）
A 垂直 B 平行 C 重合 D 相交4 两条直线被第三条直线所截，则（ ）
A 同位角相等 B 同旁内角互补
C 内错角相等 D 以上都不对夹在平行线间的两条线段相等，则两条线段所在的直线的位置关系是（ ）
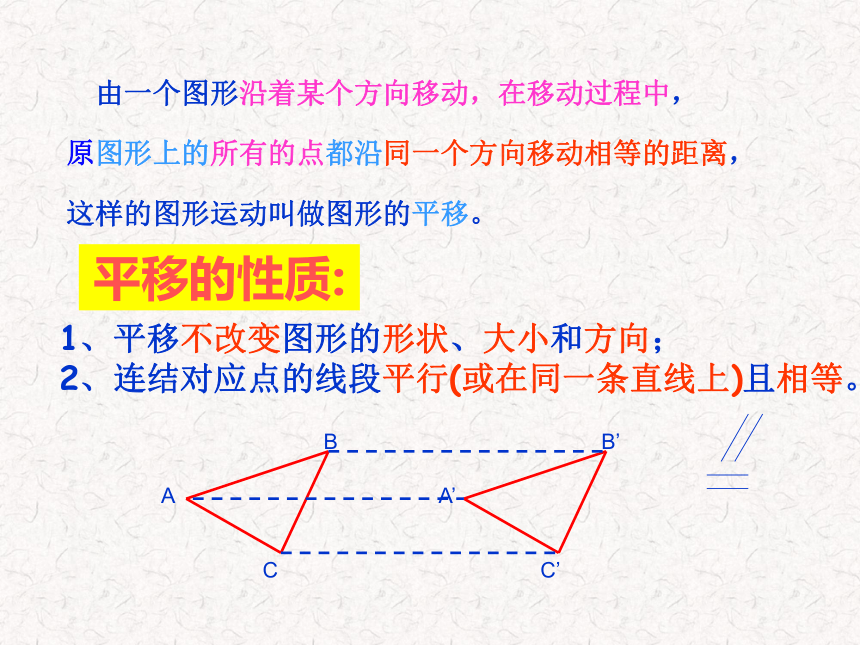
A 平行 B 相交 C 平行或相交 D不能确定　由一个图形沿着某个方向移动，在移动过程中，
原图形上的所有的点都沿同一个方向移动相等的距离，
这样的图形运动叫做图形的平移。
平移的性质:1、平移不改变图形的形状、大小和方向；
2、连结对应点的线段平行(或在同一条直线上)且相等。例1：如图，已知AB// CD,AG交AB, CD于A、C，AE、CF分别平分∠BAC, ∠DCG.你能说明AE//CF的理由吗？F　变式一：AB// CD,AG交AB, CD于A、C，AE、CF分别平分∠BAC, ∠ＡＣＨ. AE和CF还平行吗？请说明理由。　变式二：若AB// CD,且ＡＥ与ＣＥ是一对同旁内角的平分线，那么ＡＥ与ＣＥ又会有怎样的位置关系？
通过例1的三题练习，你可以得到哪些结论？F若延长CE交AB于F,你发现什么？延长AE交CD于K呢？在这图中你能编一道题考考你的同桌吗？K ∠CAB =75°例2、有一条长方形纸带，按如图所示沿AB折叠时，当∠1=30°求纸带重叠部分中∠CAB的度数。折叠三角形纸片ABC，使点A落在BC边上的点F，且折痕DE∥BC。若∠B=50°，求∠BDF的度数。变式：50°50°80°例3、如图，已知CD⊥AB，GF⊥AB，DE∥BC
说明：∠1＝∠2的理由∴∠1＝∠2（等量代换）解∵CD⊥AB，GF⊥AB（已知）∴CD∥GF（在同一平面内，垂直于同一直线的两条直线平行）∴∠2＝∠DCB（两直线平行，同位角相等）∵DE∥BC（已知）∴∠1＝∠DCB（两直线平行，内错角相等）变式一: 如图，BD⊥AC，EF⊥AC，D、F分别为垂足，∠1＝∠2，试说明∠ADG ＝∠C 。解： ∵ BD⊥AC，EF⊥AC
　　∴ EF∥DB
　　∴ ∠2=∠DBC
(两直线平行,同位角相等）
　又∵ ∠1＝∠2
　　∴ ∠１=∠DBC
　　∴ DG∥BC
(内错角相等，两直线平行)
　　∴∠ADG=∠C
（两直线平行，同位角相等）变式二：如图， △ABC中， ∠B＝∠C，AE是∠DAC的平分线，那么AE ∥BC ，请说明理由。12已知:如图1， AB∥CD（1）若∠B=25 °， ∠D=45°，
则∠E = ° （2）猜想∠B、 ∠D、∠E 之间的数量关系？ （3）若图形1变形成图2， AB∥CD不变，
猜想∠B、 ∠D、∠E 之间的数量关系？ （4）若图形1变形成图3， AB∥CD不变，
猜想∠B、 ∠D、∠E 之间的数量关系？ 70 °自我挑战（5）若图形1变形成图4，AB∥CD不变，
猜想∠B、 ∠D、∠E1、 ∠E2 、 ∠E3之间的数量关系？ （6）若上述图形变形成图5，AB∥CD不变，
猜想∠B、 ∠D、∠E1、 ∠E2 、∠E3 、 …、 ∠En-1 、 ∠En之间的数量关系？ 2、如图，两平面镜а、β的夹角为θ，入射光线AO平行于β入射到а上，经两次反射后的反射光线 平行于а，则角θ=_____度