16.1.1从分数到分式
文档属性
| 名称 | 16.1.1从分数到分式 |

|
|
| 格式 | zip | ||
| 文件大小 | 677.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-07 00:00:00 | ||
图片预览







文档简介
课件21张PPT。16.1.1 从分数到分式(4) 是多项式,也是整式 ( )(1)2x是单项式,也是整式 ( )(3)2x-1是多项式,也是整式 ( )(2) 和0都是单项式,也都是整式( ) 我们学过的代数式中有单项式、多项式、整式,请你判定下列说法是否正确单项式、多项式统称整式一、复习引入(约2分钟)√√√√(6) 是多项式,也是整式 ( )(5) 是单项式,也是整式 ( )整式
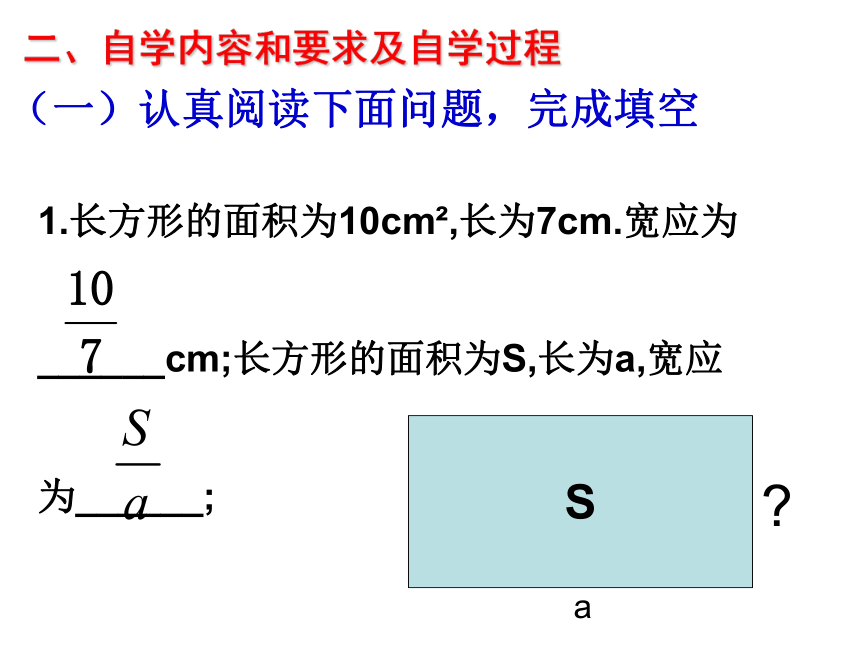
多项式单项式 既不是单项式又不是多项式,即不是整式的另一类式子××1.长方形的面积为10cm2,长为7cm.宽应为
______cm;长方形的面积为S,长为a,宽应
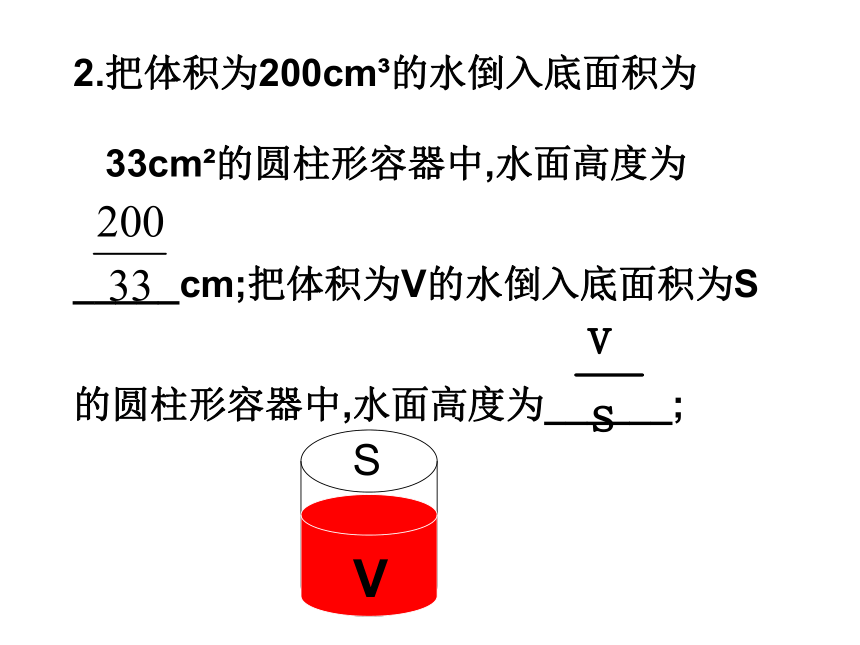
为______; 二、自学内容和要求及自学过程(一)认真阅读下面问题,完成填空2.把体积为200cm3的水倒入底面积为
33cm2的圆柱形容器中,水面高度为
_____cm;把体积为V的水倒入底面积为S
的圆柱形容器中,水面高度为______; 一艘轮船在静水中的最大航速是20千米/时,它沿江以最大船速顺流航行100千米所用时间,与以最大航速逆流航行60千米所用的时间相等。江水的流速是多少?如果设江水的流速为v千米/时。(二)认真阅读下面问题完成请大家观察式子 和 ,有什么特点?请大家观察式子 和 ,有什么特点?他们与分数有什么相同点和不同点?都具有分数的形式相同点不同点(观察分母)分母中有字母三、议一议 一般地,如果A、B表示两个整式,并且B中含有字母,那么式子 叫做分式。其中A叫做分式的分子,B为分式的分母。注意:
1. A、B均为整式,A中可含字母也可不含,但B中必须含有字母,这也是分式与整式的根本区别
2. B中所含字母为表示不同数字的字母
3. 分式是不同于整式的另一类有理式
4. 判断一个式子是否是分式时,还要注意不能先约分.
如: 是分式四、概念部分分母中是否含有字母判断:下面的式子哪些是分式哪些不是?如何区别?分式:(五)例题设计——理解分式的概念结论1:分式 有意义的条件:分母不等
于零,即B≠0时,分式 有意义;(六)用类比分数的有关知识 探索(1)分式中的分母应满足什么条件?例题——分式有意义的条件的应用 结论2:分式 无意义的条件:分母等
于零,即B=0时,分式 无意义;该怎样做?变式练习 若把题目要求改为:“当 取何值时以上分式无意义?” 探索(2)(2) 当x为何值时,分式有意义? (1) 当x为何值时,分式无意义?例1. 已知分式 , (2)由(1)得 当x ≠-2时,分式有意义 ∴当x = -2时分式:解:(1)当分母等于零时,分式无意义。∴ x = -2即 x+2=0例2. 已知分式 ,(4) 当x= - 3时,分式的值是多少?(3) 当x为何值时,分式的值为零?(4)当x = -3时,解:(3)当分子等于零而分母不
等于零时,分式的值为零。∴ x ≠ -2而 x+2≠0∴ x = ±2则 x2 - 4=0 探索(3)1.分式 的分母有什么条件限制?当B=0时, 分式 无意义.
当B≠0时,分式 有意义.?思考: 因为零不能作为除数,所以分数的分母不能是零。 在分式中分式的分母表示除数,由于除数不能为0,所以分式的分母不能为0,分式中的分母如果是零,则分式没有意义。2.当 =0时,分子和分母应满足什么条件?当A=0而B≠0时,分式 的值为零.巧学速记:
分式形状像分数,
分母为零无意义,
分式的值要为零,
分子为零母不零,
二者缺一都不行。 探索(4)附加问题 分式 在什么条件下值为负?★ 学习内容:分式的概念 数学思想:类比1.分式 有意义的条件是__________.3.分式 值为0的条件是_____________.2.分式 无意义的条件是__________.三、归纳小结(约2分钟) 探索(4)附加问题 分式 在什么条件下值为负?练
一
练
多项式单项式 既不是单项式又不是多项式,即不是整式的另一类式子××1.长方形的面积为10cm2,长为7cm.宽应为
______cm;长方形的面积为S,长为a,宽应
为______; 二、自学内容和要求及自学过程(一)认真阅读下面问题,完成填空2.把体积为200cm3的水倒入底面积为
33cm2的圆柱形容器中,水面高度为
_____cm;把体积为V的水倒入底面积为S
的圆柱形容器中,水面高度为______; 一艘轮船在静水中的最大航速是20千米/时,它沿江以最大船速顺流航行100千米所用时间,与以最大航速逆流航行60千米所用的时间相等。江水的流速是多少?如果设江水的流速为v千米/时。(二)认真阅读下面问题完成请大家观察式子 和 ,有什么特点?请大家观察式子 和 ,有什么特点?他们与分数有什么相同点和不同点?都具有分数的形式相同点不同点(观察分母)分母中有字母三、议一议 一般地,如果A、B表示两个整式,并且B中含有字母,那么式子 叫做分式。其中A叫做分式的分子,B为分式的分母。注意:
1. A、B均为整式,A中可含字母也可不含,但B中必须含有字母,这也是分式与整式的根本区别
2. B中所含字母为表示不同数字的字母
3. 分式是不同于整式的另一类有理式
4. 判断一个式子是否是分式时,还要注意不能先约分.
如: 是分式四、概念部分分母中是否含有字母判断:下面的式子哪些是分式哪些不是?如何区别?分式:(五)例题设计——理解分式的概念结论1:分式 有意义的条件:分母不等
于零,即B≠0时,分式 有意义;(六)用类比分数的有关知识 探索(1)分式中的分母应满足什么条件?例题——分式有意义的条件的应用 结论2:分式 无意义的条件:分母等
于零,即B=0时,分式 无意义;该怎样做?变式练习 若把题目要求改为:“当 取何值时以上分式无意义?” 探索(2)(2) 当x为何值时,分式有意义? (1) 当x为何值时,分式无意义?例1. 已知分式 , (2)由(1)得 当x ≠-2时,分式有意义 ∴当x = -2时分式:解:(1)当分母等于零时,分式无意义。∴ x = -2即 x+2=0例2. 已知分式 ,(4) 当x= - 3时,分式的值是多少?(3) 当x为何值时,分式的值为零?(4)当x = -3时,解:(3)当分子等于零而分母不
等于零时,分式的值为零。∴ x ≠ -2而 x+2≠0∴ x = ±2则 x2 - 4=0 探索(3)1.分式 的分母有什么条件限制?当B=0时, 分式 无意义.
当B≠0时,分式 有意义.?思考: 因为零不能作为除数,所以分数的分母不能是零。 在分式中分式的分母表示除数,由于除数不能为0,所以分式的分母不能为0,分式中的分母如果是零,则分式没有意义。2.当 =0时,分子和分母应满足什么条件?当A=0而B≠0时,分式 的值为零.巧学速记:
分式形状像分数,
分母为零无意义,
分式的值要为零,
分子为零母不零,
二者缺一都不行。 探索(4)附加问题 分式 在什么条件下值为负?★ 学习内容:分式的概念 数学思想:类比1.分式 有意义的条件是__________.3.分式 值为0的条件是_____________.2.分式 无意义的条件是__________.三、归纳小结(约2分钟) 探索(4)附加问题 分式 在什么条件下值为负?练
一
练
