北师大版九年级数学下册 4 解直角三角形课件(共31张PPT)
文档属性
| 名称 | 北师大版九年级数学下册 4 解直角三角形课件(共31张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-25 06:14:51 | ||
图片预览







文档简介
(共31张PPT)
直角三角形的边角关系
复习指导。
1.什么是锐角三角函数?与斜坡(或梯子)的倾斜度有何关系?
2.理解仰角、俯角、方向角、坡角、坡度的含义。
3.熟记30°、45°、60°角的三角函数值,
提纲导学,自主学习
提纲导学,自主学习
1、锐角三角函数:
在Rt△ABC中,∠C是直角,如图
(1)正弦:∠A的____与____的比叫做∠A的正弦,记作sinA,即sinA= _____;
(2)余弦:∠A的_____与_____的比叫做∠A的余弦,记作cosA,即cosA=_______;
(3)正切:∠A的____与____的比叫做∠A的正切,记作tanA,即tanA=_______;
A
B
C
a
b
┌
c
对边
斜边
斜边
对边
邻边
邻边
锐角三角函数:锐角A的正弦、余弦、正切都叫做∠A的______三角函数.
正切值越_____,梯子越陡;
正弦值越_____,梯子越陡;
余弦值越_____,梯子越陡;
提纲导学,自主学习
锐角
大
大
小
提纲导学,自主学习
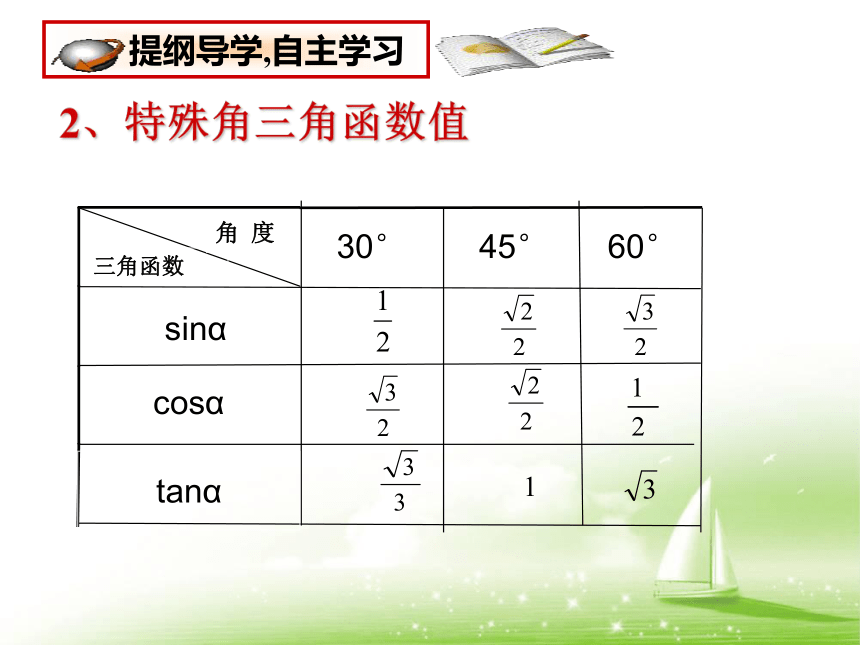
cosα
sinα
60°
角 度
三角函数
2、特殊角三角函数值
1
45°
30°
tanα
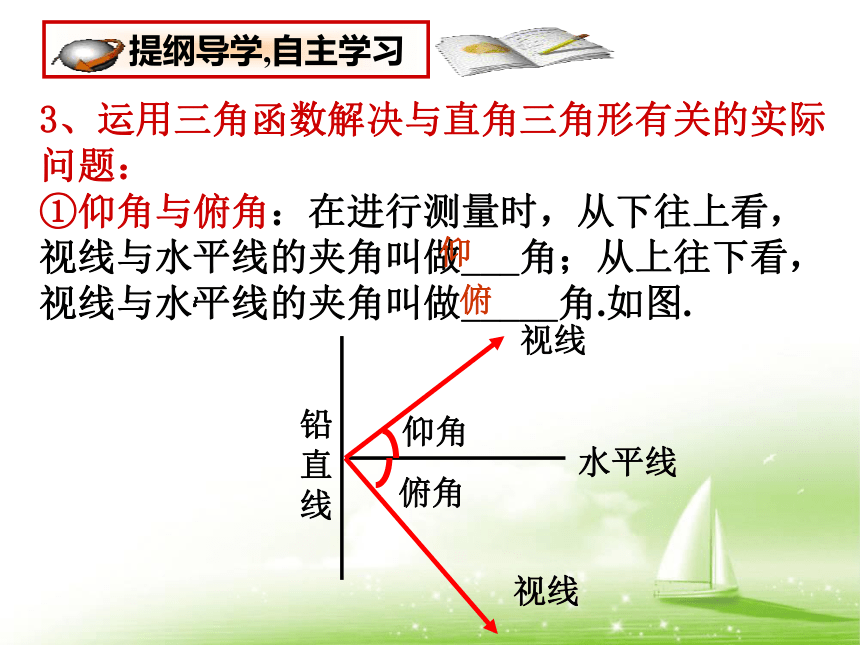
3、运用三角函数解决与直角三角形有关的实际问题:
①仰角与俯角:在进行测量时,从下往上看,视线与水平线的夹角叫做___角;从上往下看,视线与水平线的夹角叫做_____角.如图.
提纲导学,自主学习
仰
俯
铅直线
水平线
视线
视线
仰角
俯角
②坡角与坡度:坡面与水平面的夹角叫做___角,图中的 α 是坡角;坡面的____高度h和_____距离l的比叫坡度。
即:i=______=_______
提纲导学,自主学习
l
h
┌
α
i
坡
铅直
水平
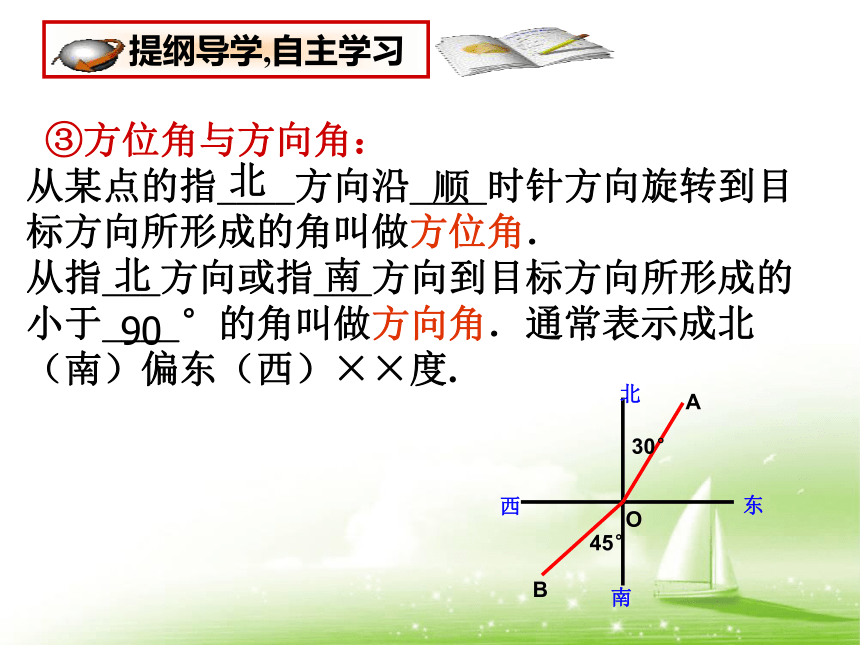
③方位角与方向角:
从某点的指____方向沿____时针方向旋转到目标方向所形成的角叫做方位角.
从指___方向或指___方向到目标方向所形成的小于____°的角叫做方向角.通常表示成北(南)偏东(西)××度.
提纲导学,自主学习
30°
45°
B
O
A
东
西
北
南
北
顺
北
南
90
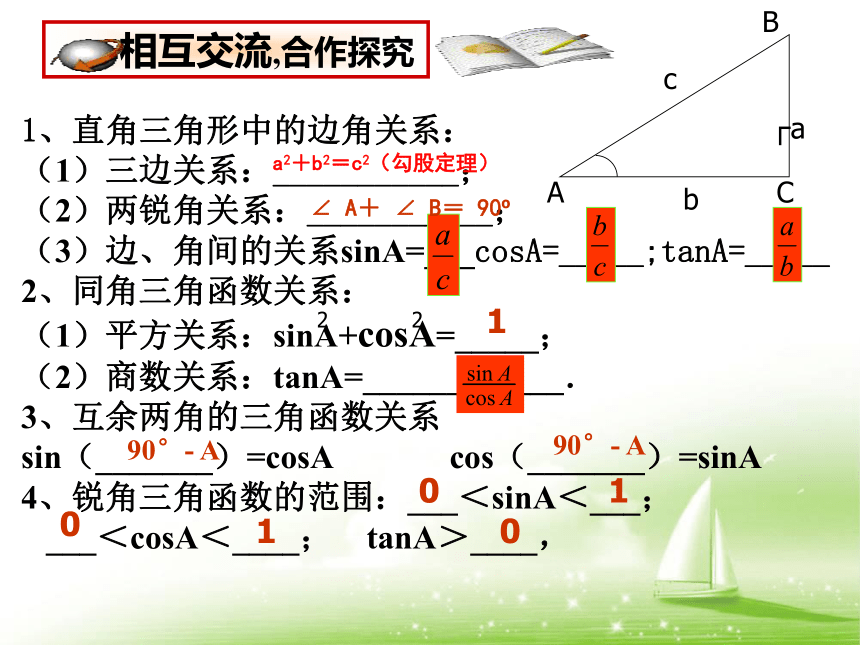
1、直角三角形中的边角关系:
(1)三边关系:___________;
(2)两锐角关系:___________;
(3)边、角间的关系sinA=___cosA=_____;tanA=_____
2、同角三角函数关系:
(1)平方关系:sinA+cosA=_____;
(2)商数关系:tanA=____________.
3、互余两角的三角函数关系
sin(_______)=cosA cos(_______)=sinA
4、锐角三角函数的范围:___<sinA<___;
___<cosA<____; tanA>____,
相互交流,合作探究
2
2
A
B
C
a
b
┌
c
a2+b2=c2(勾股定理)
∠ A+ ∠ B= 90
90°- A
90°- A
0
0
1
1
0
1
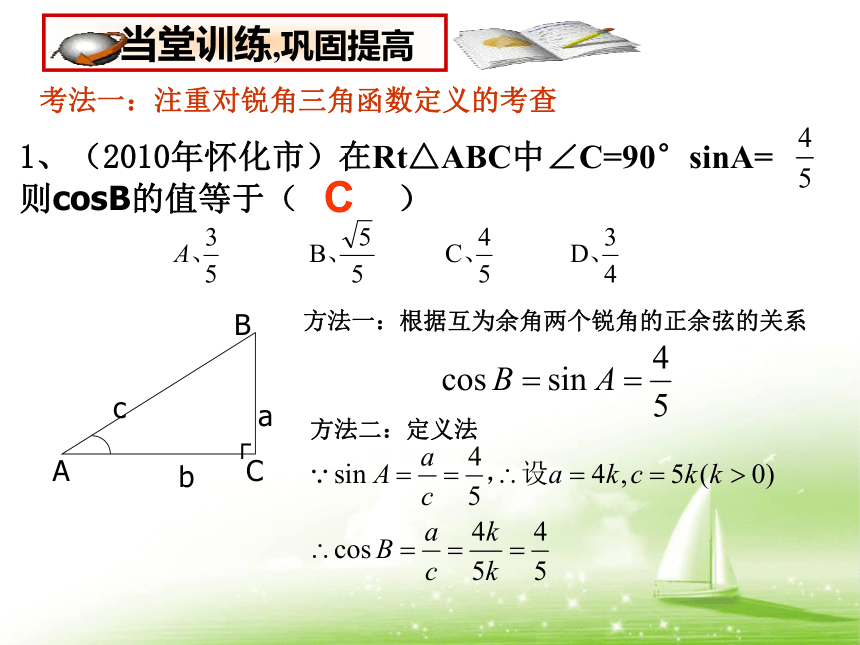
1、(2010年怀化市)在Rt△ABC中∠C=90°sinA=
则cosB的值等于( )
C
考法一:注重对锐角三角函数定义的考查
A
B
C
a
b
┌
c
方法一:根据互为余角两个锐角的正余弦的关系
方法二:定义法
当堂训练,巩固提高
2、(2011江苏苏州)如图,在四边形ABCD中,E、F分别是AB、AD的中点,若EF=2,BC=5,CD=3,则tanC等于( )
A. B. C. D.
B
解:连接BD,∵E、F分别为AB、AD中点,∴BD=2EF=2×2=4
3、在△ABC中,∠C=90°,则sinA+cosA的( )
A.等于1 B.大于1 C.小于1 D.不一定
B
方法一:定义法
方法二:特殊值法:
A
B
C
a
b
┌
c
4.(2010湖北省咸宁市)如图,已知直l1‖l2‖l3‖l4相邻两条平行直线间的距离都是1,如果正方形ABCD
的四个顶点分别在四条直线上,则sinα=_____。
E
F
分析:分别作BE⊥l1,DF⊥l1,垂足分别为E、F
易证:△DFA≌△AEB
∴AF=BE=2
在Rt△DFA中由勾股定理得:
1、(2011湖北黄冈)cos30°=( )
C
考法二:注重对特殊角的三角函数值的考查
2、(2010年怀化市)在Rt△ABC中,∠C=90°,sinA= 则∠A=______
3、(2008年郴州市)计算:
1、如图所示,某河堤的横断面是梯形ABCD,BC‖AD,
迎水坡AB长13米,且迎水坡AB的坡度为12:5,∠D= 则背水坡CD的长为_______米。
24
分析:分别作BE⊥AD,CF⊥AD,垂足分别为E、F
E
F
由四边形BEFC为矩形得CF=BE=12米
考法三:重点考查锐角三角函数在实际问题中的应用
2、如图为了测量小河的宽度,在河的岸边选择B、C两点,在对岸选择一个目标点A,测得∠ABC=60°, ∠ACB=45°,BC=( )米,求小河的宽度。
解:过点A作AD⊥BC,垂足为D,设小河的宽度AD=x米
D
1、如图,小鸣将测倾器安放在与旗杆AB底部相距6m的C处,量出测倾器的高度CD=1m,测得旗杆顶端B的仰角α=45°,则旗杆AB的高度为_____m.
考法四:利用测量高度问题考查解直角三角形
7
2、如图,一艘渔船以6海里/时的速度至西向东航行,小岛周围 海里内有暗礁,渔船在A处,测得小岛P在北偏东60°方向上,航行2小时后在B处,测得小岛P在北偏东30°方向上,如果渔船不改变航向有没有触礁危险?
C
解:过点P作PC⊥AB,交AB延长线于C点,根据垂线段最短知PC就是最近距离
分组讨论 ,合作交流
3、如图,山上有一座铁塔,山脚下有一矩形建筑物ABCD,且建筑物周围没有开阔平整地带.该建筑物顶端宽度AD和高度DC都可直接测得,从A、D、C三点可看到塔顶端H.可供使用的测量工具有皮尺、测倾器.
请你根据现有条件,充分利用矩形建筑物,设计一个测量塔顶端到地面高度HG的方案.具体要求如下:
①测量数据尽可能少;
②在所给图形上,画出你设计的测量平面图,并将应测数据标记在图形上(如果测A、D间距离,用m表示;如果测D、C间距离,用n表示;如果测角,用α、β、γ表示).
A
H
G
B
D
C
α
β
n
方案1图a
M
H
A
G
B
D
C
α
γ
n
m
方案2图b
M
H
A
G
B
D
C
α
γ
n
m
β
方案3图c
M
A
H
G
B
D
C
α
β
n
M
图d
图e
A
H
G
B
D
C
γ
β
n
M
m
锐角三角函数
特殊角的三角函数
解直角三角形
简单实际问题
c
a
b
A
B
C
知识梳理
1、本节例题学习以后,我们可以得到解直角三角形的基本图形:
2、作高线可以把平行四边形、梯形转化为含直角三角形的图形.
3、解直角三角形应用的解题思路:
数学模型
简单实际问题
直角三角形
构建
解
从组合直角三角形中寻找公共边是解决问题的关键;方程是解决问题的有效方法。
1、(2010年怀化市)在Rt△ABC中∠C=90°sinA= 则tanB的值等于( )
2、(2011山东烟台)如果△ABC中,sinA=cosB= ,则下列最确切的结论是( )
A. △ABC是直角三角形 B. △ABC是等腰三角形
C. △ABC是等腰直角三角形 D. △ABC是锐角三角形
3、(20011江苏镇江)∠α的补角是120°,则∠α=______,sinα=______.
4、(2009沈阳市)如图,市政府准备修建一座高AB=6m的过街天桥,已知天桥的坡面AC与地面BC的夹角∠ACB的正弦值为0.6,则坡面AC长度为
m.
B
C
60°
10
5、(2010年济宁市)计算:
6、在玉树地震灾区,抢险队派一架直升飞机去A、B两个村庄抢险,飞机在距地面450米上空的P点,测得A村的俯角为 ,B村的俯角为 (如图).求A、B两个村庄间的距离.(结果精确到个位,参考数据 )
当堂自测 ,检验效果
5
520米
直角三角形的边角关系
复习指导。
1.什么是锐角三角函数?与斜坡(或梯子)的倾斜度有何关系?
2.理解仰角、俯角、方向角、坡角、坡度的含义。
3.熟记30°、45°、60°角的三角函数值,
提纲导学,自主学习
提纲导学,自主学习
1、锐角三角函数:
在Rt△ABC中,∠C是直角,如图
(1)正弦:∠A的____与____的比叫做∠A的正弦,记作sinA,即sinA= _____;
(2)余弦:∠A的_____与_____的比叫做∠A的余弦,记作cosA,即cosA=_______;
(3)正切:∠A的____与____的比叫做∠A的正切,记作tanA,即tanA=_______;
A
B
C
a
b
┌
c
对边
斜边
斜边
对边
邻边
邻边
锐角三角函数:锐角A的正弦、余弦、正切都叫做∠A的______三角函数.
正切值越_____,梯子越陡;
正弦值越_____,梯子越陡;
余弦值越_____,梯子越陡;
提纲导学,自主学习
锐角
大
大
小
提纲导学,自主学习
cosα
sinα
60°
角 度
三角函数
2、特殊角三角函数值
1
45°
30°
tanα
3、运用三角函数解决与直角三角形有关的实际问题:
①仰角与俯角:在进行测量时,从下往上看,视线与水平线的夹角叫做___角;从上往下看,视线与水平线的夹角叫做_____角.如图.
提纲导学,自主学习
仰
俯
铅直线
水平线
视线
视线
仰角
俯角
②坡角与坡度:坡面与水平面的夹角叫做___角,图中的 α 是坡角;坡面的____高度h和_____距离l的比叫坡度。
即:i=______=_______
提纲导学,自主学习
l
h
┌
α
i
坡
铅直
水平
③方位角与方向角:
从某点的指____方向沿____时针方向旋转到目标方向所形成的角叫做方位角.
从指___方向或指___方向到目标方向所形成的小于____°的角叫做方向角.通常表示成北(南)偏东(西)××度.
提纲导学,自主学习
30°
45°
B
O
A
东
西
北
南
北
顺
北
南
90
1、直角三角形中的边角关系:
(1)三边关系:___________;
(2)两锐角关系:___________;
(3)边、角间的关系sinA=___cosA=_____;tanA=_____
2、同角三角函数关系:
(1)平方关系:sinA+cosA=_____;
(2)商数关系:tanA=____________.
3、互余两角的三角函数关系
sin(_______)=cosA cos(_______)=sinA
4、锐角三角函数的范围:___<sinA<___;
___<cosA<____; tanA>____,
相互交流,合作探究
2
2
A
B
C
a
b
┌
c
a2+b2=c2(勾股定理)
∠ A+ ∠ B= 90
90°- A
90°- A
0
0
1
1
0
1
1、(2010年怀化市)在Rt△ABC中∠C=90°sinA=
则cosB的值等于( )
C
考法一:注重对锐角三角函数定义的考查
A
B
C
a
b
┌
c
方法一:根据互为余角两个锐角的正余弦的关系
方法二:定义法
当堂训练,巩固提高
2、(2011江苏苏州)如图,在四边形ABCD中,E、F分别是AB、AD的中点,若EF=2,BC=5,CD=3,则tanC等于( )
A. B. C. D.
B
解:连接BD,∵E、F分别为AB、AD中点,∴BD=2EF=2×2=4
3、在△ABC中,∠C=90°,则sinA+cosA的( )
A.等于1 B.大于1 C.小于1 D.不一定
B
方法一:定义法
方法二:特殊值法:
A
B
C
a
b
┌
c
4.(2010湖北省咸宁市)如图,已知直l1‖l2‖l3‖l4相邻两条平行直线间的距离都是1,如果正方形ABCD
的四个顶点分别在四条直线上,则sinα=_____。
E
F
分析:分别作BE⊥l1,DF⊥l1,垂足分别为E、F
易证:△DFA≌△AEB
∴AF=BE=2
在Rt△DFA中由勾股定理得:
1、(2011湖北黄冈)cos30°=( )
C
考法二:注重对特殊角的三角函数值的考查
2、(2010年怀化市)在Rt△ABC中,∠C=90°,sinA= 则∠A=______
3、(2008年郴州市)计算:
1、如图所示,某河堤的横断面是梯形ABCD,BC‖AD,
迎水坡AB长13米,且迎水坡AB的坡度为12:5,∠D= 则背水坡CD的长为_______米。
24
分析:分别作BE⊥AD,CF⊥AD,垂足分别为E、F
E
F
由四边形BEFC为矩形得CF=BE=12米
考法三:重点考查锐角三角函数在实际问题中的应用
2、如图为了测量小河的宽度,在河的岸边选择B、C两点,在对岸选择一个目标点A,测得∠ABC=60°, ∠ACB=45°,BC=( )米,求小河的宽度。
解:过点A作AD⊥BC,垂足为D,设小河的宽度AD=x米
D
1、如图,小鸣将测倾器安放在与旗杆AB底部相距6m的C处,量出测倾器的高度CD=1m,测得旗杆顶端B的仰角α=45°,则旗杆AB的高度为_____m.
考法四:利用测量高度问题考查解直角三角形
7
2、如图,一艘渔船以6海里/时的速度至西向东航行,小岛周围 海里内有暗礁,渔船在A处,测得小岛P在北偏东60°方向上,航行2小时后在B处,测得小岛P在北偏东30°方向上,如果渔船不改变航向有没有触礁危险?
C
解:过点P作PC⊥AB,交AB延长线于C点,根据垂线段最短知PC就是最近距离
分组讨论 ,合作交流
3、如图,山上有一座铁塔,山脚下有一矩形建筑物ABCD,且建筑物周围没有开阔平整地带.该建筑物顶端宽度AD和高度DC都可直接测得,从A、D、C三点可看到塔顶端H.可供使用的测量工具有皮尺、测倾器.
请你根据现有条件,充分利用矩形建筑物,设计一个测量塔顶端到地面高度HG的方案.具体要求如下:
①测量数据尽可能少;
②在所给图形上,画出你设计的测量平面图,并将应测数据标记在图形上(如果测A、D间距离,用m表示;如果测D、C间距离,用n表示;如果测角,用α、β、γ表示).
A
H
G
B
D
C
α
β
n
方案1图a
M
H
A
G
B
D
C
α
γ
n
m
方案2图b
M
H
A
G
B
D
C
α
γ
n
m
β
方案3图c
M
A
H
G
B
D
C
α
β
n
M
图d
图e
A
H
G
B
D
C
γ
β
n
M
m
锐角三角函数
特殊角的三角函数
解直角三角形
简单实际问题
c
a
b
A
B
C
知识梳理
1、本节例题学习以后,我们可以得到解直角三角形的基本图形:
2、作高线可以把平行四边形、梯形转化为含直角三角形的图形.
3、解直角三角形应用的解题思路:
数学模型
简单实际问题
直角三角形
构建
解
从组合直角三角形中寻找公共边是解决问题的关键;方程是解决问题的有效方法。
1、(2010年怀化市)在Rt△ABC中∠C=90°sinA= 则tanB的值等于( )
2、(2011山东烟台)如果△ABC中,sinA=cosB= ,则下列最确切的结论是( )
A. △ABC是直角三角形 B. △ABC是等腰三角形
C. △ABC是等腰直角三角形 D. △ABC是锐角三角形
3、(20011江苏镇江)∠α的补角是120°,则∠α=______,sinα=______.
4、(2009沈阳市)如图,市政府准备修建一座高AB=6m的过街天桥,已知天桥的坡面AC与地面BC的夹角∠ACB的正弦值为0.6,则坡面AC长度为
m.
B
C
60°
10
5、(2010年济宁市)计算:
6、在玉树地震灾区,抢险队派一架直升飞机去A、B两个村庄抢险,飞机在距地面450米上空的P点,测得A村的俯角为 ,B村的俯角为 (如图).求A、B两个村庄间的距离.(结果精确到个位,参考数据 )
当堂自测 ,检验效果
5
520米
