北师大版九年级数学下册第一章《直角三角形的边角关系》复习课件2(共41张PPT)
文档属性
| 名称 | 北师大版九年级数学下册第一章《直角三角形的边角关系》复习课件2(共41张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-24 23:19:46 | ||
图片预览




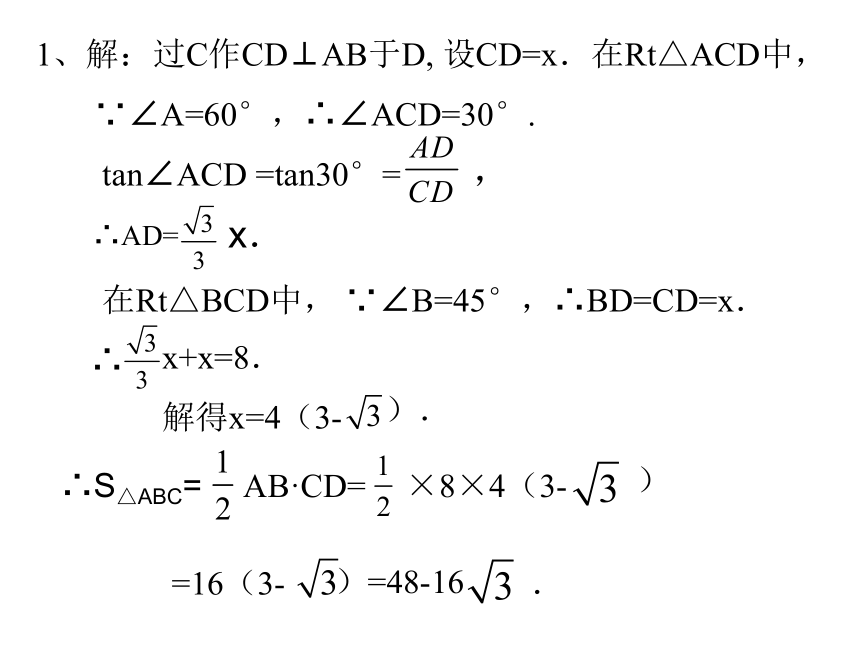

文档简介
(共41张PPT)
复习回顾:
1、什么叫函数?函数有哪三种表示法?
2、三角函数为什么是函数 自变量是什么?因变量呢?
3、三角函数中自变量的取值范围是什么?因变量呢?
4、三角函数间有那些关系?如何证明?
三边之间的关系
a2+b2=c2(勾股定理);
锐角之间的关系
∠A+∠B=90
边角之间的关系(锐角三角函数)
tanA=
a
b
sinA=
a
c
1、
cosA=
b
c
A
C
B
a
b
c
解直角三角形的依据
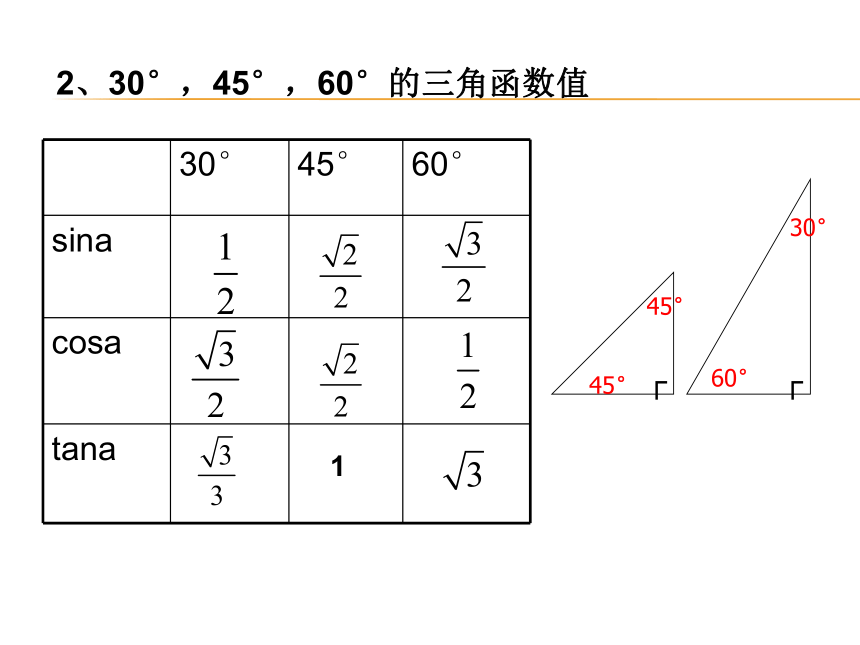
2、30°,45°,60°的三角函数值
30° 45° 60°
sina
cosa
tana
1
┌
┌
45°
45°
30°
60°
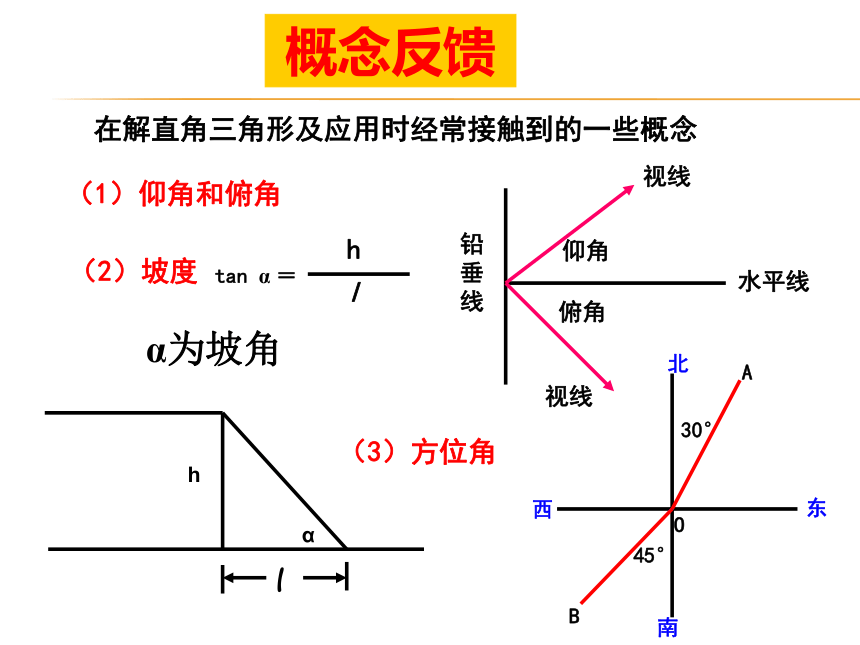
在解直角三角形及应用时经常接触到的一些概念
l
h
α
(2)坡度
tan α =
h
l
概念反馈
(1)仰角和俯角
视线
铅垂线
水平线
视线
仰角
俯角
(3)方位角
30°
45°
B
O
A
东
西
北
南
α为坡角
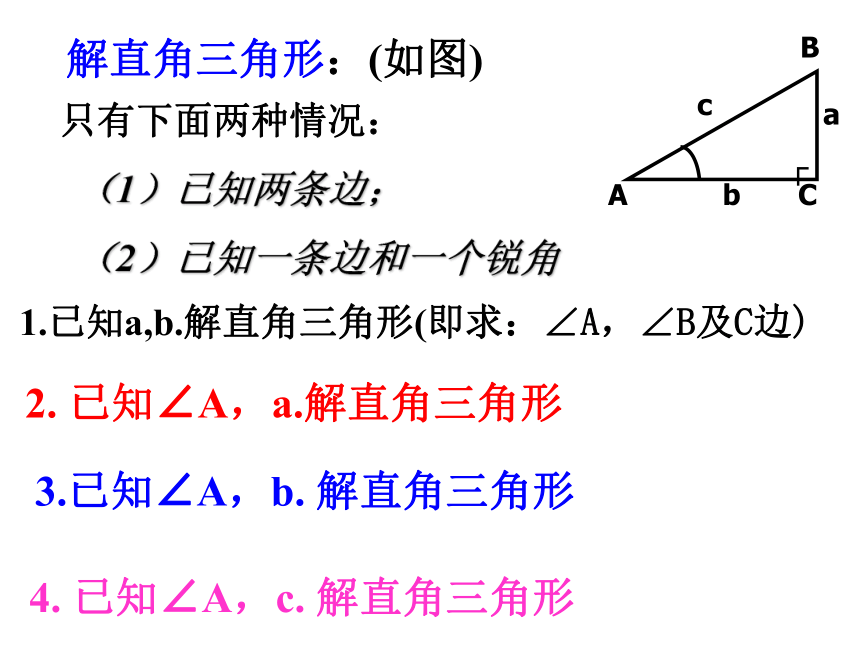
解直角三角形:(如图)
1.已知a,b.解直角三角形(即求:∠A,∠B及C边)
2. 已知∠A,a.解直角三角形
3.已知∠A,b. 解直角三角形
4. 已知∠A,c. 解直角三角形
b
A
B
C
a
┌
c
只有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角
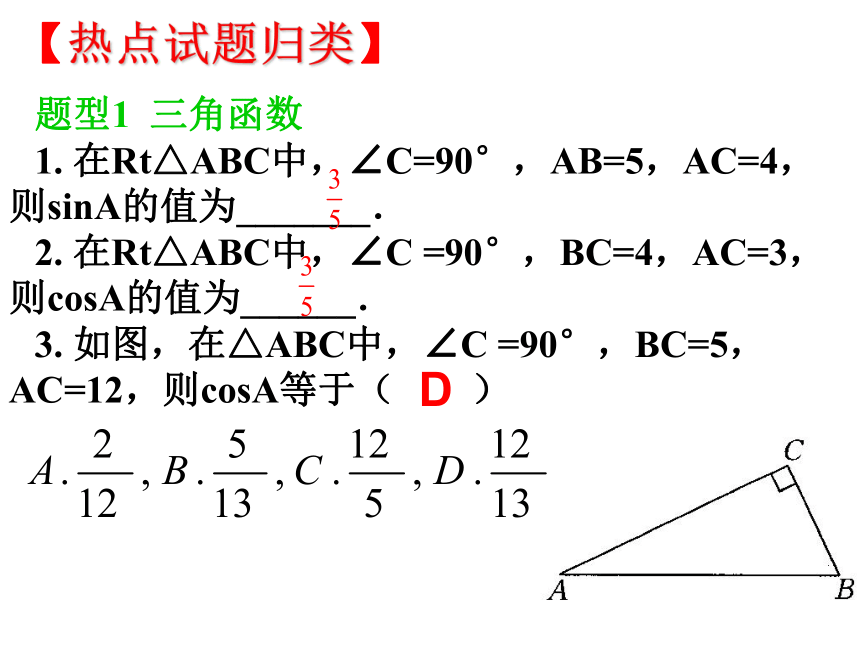
【热点试题归类】
题型1 三角函数
1. 在Rt△ABC中,∠C=90°,AB=5,AC=4,则sinA的值为_______.
2. 在Rt△ABC中,∠C =90°,BC=4,AC=3,则cosA的值为______.
3. 如图,在△ABC中,∠C =90°,BC=5,AC=12,则cosA等于( )
D
4. 如图,在Rt△ABC中,∠ACB =90°,CD⊥AB于点D,已知AC=
BC=2,那么sin∠ABC=( )
,
A.
A.tan∠AED B.tan∠AEB
C.sin∠AED D.cos∠AED
5. 如图所示,AB是⊙O的直径,弦AC、BD相交于E,则
等于( )
6.计算:
|-
|+(cos60°-tan30°)0+
.
A
D
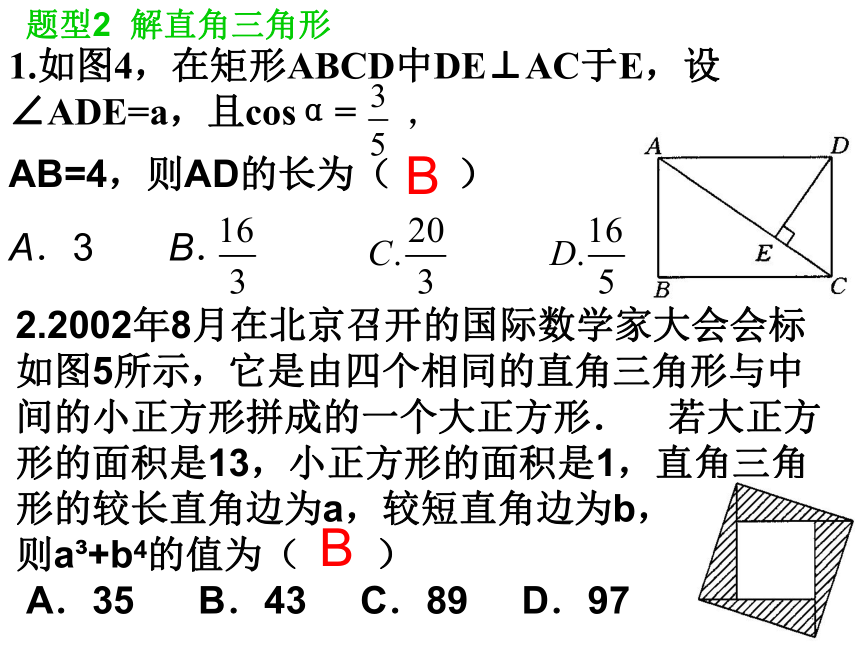
题型2 解直角三角形
1.如图4,在矩形ABCD中DE⊥AC于E,设∠ADE=a,且cosα=
AB=4,则AD的长为( )
,
A.3 B.
2.2002年8月在北京召开的国际数学家大会会标如图5所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是13,小正方形的面积是1,直角三角形的较长直角边为a,较短直角边为b,
则a +b4的值为( )
A.35 B.43 C.89 D.97
B
B
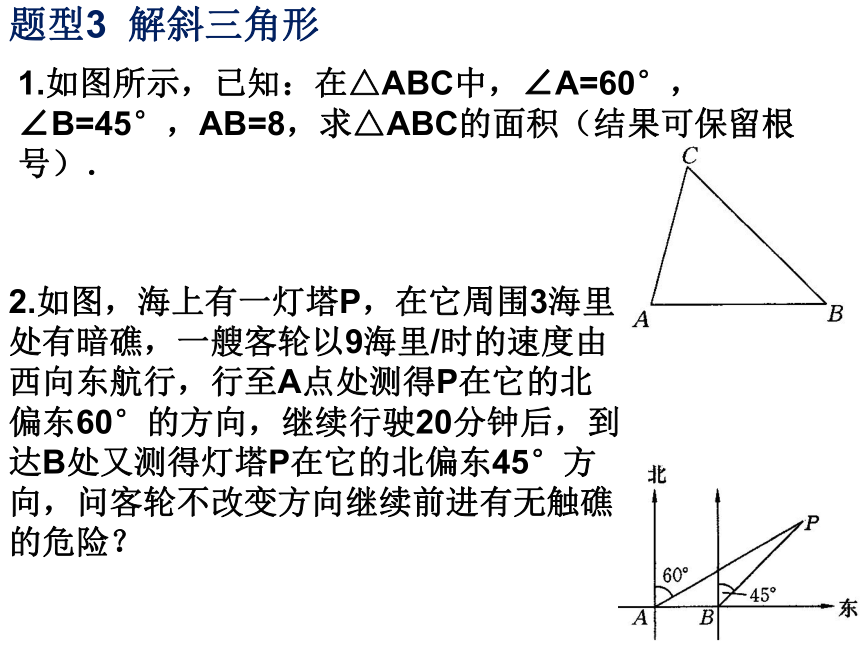
题型3 解斜三角形
1.如图所示,已知:在△ABC中,∠A=60°,∠B=45°,AB=8,求△ABC的面积(结果可保留根号).
2.如图,海上有一灯塔P,在它周围3海里处有暗礁,一艘客轮以9海里/时的速度由西向东航行,行至A点处测得P在它的北偏东60°的方向,继续行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向,问客轮不改变方向继续前进有无触礁的危险?
1、解:过C作CD⊥AB于D, 设CD=x.在Rt△ACD中,
∵∠A=60°,∴∠ACD=30°.
tan∠ACD =tan30°=
在Rt△BCD中, ∵∠B=45°,∴BD=CD=x.
∴
x+x=8.
解得x=4(3-
).
=16(3-
)=48-16
.
,
∴AD=
x.
AB·CD=
×8×4(3-
∴S△ABC=
)
2.解:过P作PC⊥AB于C点,据题意知:
AB=9×
=3,∠PAB=90°-60°=30°,
∠PBC=90°-45°=45°,∠PCB=90°.
∴PC=BC.
在Rt△APC中,
PC>3.
∴客轮不改变方向继续前进无触礁危险.
tan30°=
,
即
=
,
3.如图,某校九年级3班的一个学生小组进行测量小山高度的实践活动.部分同学在山脚点A测得山腰上一点D的仰角为30°,并测得AD的长度为180米;另一部分同学在山顶点B测得山脚点A的俯角为45°,山腰点D的俯角为60°.请你帮助他们计算出小山的高度BC(计算过程和结果都不取近似值).
在Rt△ADF中,AD=180,∠DAF=30°,
∴DF=90,AF=90
3.解:如图设BC=x,
解得x=90
+90.
(x-90).
FC=AC-AF=x-90
.
∵∠BAC=∠ABC=45°,
∴AC=BC=x.
∴BE=BC-EC=x-90.
在Rt△BDE中,∠BDE=60°,
∴DE=
BE=
.
(x-90)=x-90
∵DE=FC,
∴
.
4.如图,在观测点E测得小山上铁塔顶A的仰角为60°,铁塔底部B的仰角为45°.已知塔高AB=20m,观察点E到地面的距离EF=35m,求小山BD的高(精确到0.1m,
≈1.732).
4.解:如图,过C点作CE⊥AD于C.
x-x.
解得x=10
∵AB=AC-BC,
即20=
∴BD=BC+CD=BC+EF
设BC=x,则EC=BC=x.
在Rt△ACE中,AC=
x,
+10.
+10+35≈45+10×1.732≈62.3(m).
所以小山BD的高为62.3m.
=10
题型4 应用举例
1.有人说,数学家就是不用爬树或把树砍倒就能够知道树高的人.小敏想知道校园内一棵大树的高(如图),她测得CB=10米,∠ACB=50°,请你帮助她算出树高AB约为________米.(注:①树垂直于地面;②供选用数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.2)
12
2.如图,小华为了测量所住楼房的高度,他请来同学帮忙,测量了同一时刻他自己的影长和楼房的影长分别是0.5米和15米,已知小华的身高为1.6米,那么分所住楼房的
高度为________米.
3.如图,两建筑物AB和CD的水平距离为30米,从A点测得D点的俯角为30°,测得C点的俯角为60°,则建筑物CD的高为______米.
48
20
4.如图,花丛中有一路灯杆AB.在灯光下,小明在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时小明的影长GH=5米.如果小明的身高为1.7米,求路灯杆AB的高度(精确到0.1米).
4.解:设AB=x米,BD=y米.
由△CDE∽△ABE得
. ①
由△FGH∽△ABH得
. ②
由①,②得y=7.5,x=5.95≈6.0米.
所以路灯杆AB的高度约为6.0米.
5.如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点.已知∠BAC=65°,∠DAE=45°,点D到地面的垂直距离DE=3 m,求点B到地面的垂直距离BC(精确到0.1m).
5.解:在Rt△ADE中,DE=3
∠DAE=45°,
∴sin∠DAE=
∴AD=6.
又∵AD=AB,
在Rt△ABC中,sin∠BAC=
∴BC=AB·sin∠BAC=6·sin65°≈5.4.
答:点B到地面的垂直距离BC约为5.4米.
,
,
,
6.如图,我市某广场一灯柱AB被一钢缆CD固定,CD与地面成40°夹角,且DB=5m,现要在C点上方2m处加固另一条钢缆ED,那么EB的高为多少米?(结果保留三个有效数字)
6.解:在Rt△BCD中,∠BDC=40°,DB=5m,
∵tan∠BDC=
∴BC=DB·tan∠BDC
=5×tan40°≈4.195.
∴EB=BC+CE=4.195+2≈6.20.
答:略.
,
7.如图,在电线杆上的C处引位线CE、CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B处安置测角仪,在A处测得电线杆C处的仰角为30°,已知测角仪AB高为1.5米,求拉线CE的长.(结果保留根号)
7.解:过点A作AH⊥CD,垂足为H.
由题意可知四边形ABDH为矩形,
∠CAH=30°,
∴AB=DH=1.5,BD=AH=6.
在Rt△ACH中,tan∠CAH=
,
∴CH=AH·tan∠CAH=6tan30°=6×
=2
在Rt△CDE中 ,
∵∠CED=60°,sin∠CED=
∴CE=
=(4+
)(米).
∵DH=1.5,∴CD=2
+1.5.
答:拉线CE的长为(4+
)米.
8.已知:如图,在山脚的C处测得山顶A的仰角为45°,沿着坡度为30°的斜坡前进400米到D处(即∠DCB=30°,CD=400米),测得A的仰角为60°,求山的高度AB.
9.如图,在一个坡角为15°的斜坡上有一棵树,高为AB.当太阳光与水平线成50°时,测得该树在斜坡的树影BC的长为7m,求树高.(精确到0.1m)
在矩形DEBF中,BE=DF=200米,
在Rt△ACB中,∠ACB=45°,
∴AB=BC,
即
8.解:如图,作DE⊥AB于E,作DF⊥BC于F,在Rt△CDF中∠DCF=30°,CD=400米,
∴DF=CD·sin30°=
×400=200(米).
CF=CD·cos30°=
×400=200 (米).
+x.
x+200=200
∴x=200,
∴AB=AE+BE=(200
+200)米.
在Rt△ADE中,∠ADE=60°,设DE=x米,
∴AE=tan60°·x=
x(米).
∵∠BCD=15°,
∴∠ACD=50°,
在Rt△CDB中,
CD=7×cos15°,
BD=7×sin15°.
在Rt△CDA中,
AD=CD×tan50°=7×cos15°×tan50°.
∴AB=AD-BD
=(7×cos15°×tan50°-7×sin15°)
=7(cos15°×tan50°-sin15°)≈6.2(m).
答:树高约为6.2m.
9.解:如图,过点C作水平线与AB的延长线交于点D,则AD⊥CD.
这节课你有哪些收获
你能否用所学的知识去解决一些
实际问题吗
题型5 综合与创新
1.小明骑自行车以15千米/小时的速度在公路上向正北方向匀速行进,如图1,出发时,在B点他观察到仓库A在他的北偏东30°处,骑行20分钟后到达C点,发现此时这座仓库正好在他的东南方向,则这座仓库到公路的距离为_____千米.(参考数据:
≈1.732,结果
保留两位有效数字)
1.8
2.先将一矩形ABCD置于直角坐标系中,使点A与坐标系的原点重合,边AB、AD分别落在x轴、y轴上(如左图),再将此矩形在坐标平面内按逆时针方向绕原点旋转30°(如右图),若AB=4,BC=3 ,则左图和右图中点B的坐标为___,点C的坐标为____.
答案:图(2)中:B(4,0),图(3)中:B(2 ,2);
图(2)中:C(4,3),图(3)中:C(
).
3.数学活动课上,小敏、小颖分别画了△ABC和△DEF,数据如图,如果把小敏画的三角形面积记作S△ABC,小颖画的三角形面积记作S△DEF,那么你认为( )
A.S△ABC >S△DEF B.S△ABCC.S△ABC =S△DEF D.不能确定
小敏画的三角形 小颖画的三角形
C
4.已知:如图,在△ABC中,AD是边BC上的高,E为边AC的中点,BC= 14,AD=12,sinB=
求:(1)线段DC的长;
(2)tan∠EDC的值.
∴CD=BC-BD=14-9=5.
(2)∵E是Rt△ADC斜边AC的中点,
∴DE=EC,∴∠EDC=∠C.
∴tan∠EDC=tan∠C=
.
4.解:(1)在Rt△ABD中,AB=
=15.
∴BD=
=9.
5.某校教学楼后面紧邻着一个土坡,坡上面是一块平地,如图所示,BC∥AD,斜坡AB长22m,坡角∠BAD=68°,为了防止山体滑坡,保障安全,学校决定对该土坡进行改造.经地质人员勘测,当坡角不超过50°时,可确保山体不滑坡.(1)求改造前坡顶与地面的距离BE的长(精确到0.1m);(2)为确保安全,学校计划改造时保持坡脚A不动,坡顶B沿BC削进到F点处,问BF至少是多少米(精确到0.1m)?
(参考数据:sin68°≈0.927 2,
cos68°≈0.374 6,tan68°≈2.475 1,
tan50°≈0.766 0,cos50°≈0.642 8,
tan50°≈1.191 8)
5.解:如图,(1)作BE⊥AD,E为垂足.
AE=AB·cos68°
=22cos68°≈8.24,
∴BF=AG-AE=8.88
≈8.9 (m).
即BF至少是8.9m.
则BE=AB·sin68°=22sin68°≈20.40=20.4(m)(2)作FG⊥AD,G为垂足,
连结FA,则FG=BE.
∵AG=
=17.12,
≈1.73)
6.如图,小岛A在港口P的南偏西45°方向,距离港口81海里处.甲船从A出发,沿AP方向以9海里/时的速度驶向港口,乙船从港口P出发,沿南偏东60°方向,以18海里/时的速度驶离港口,现两船同时出发,
(1)出发后几小时两船与港口P的距离相等?
(2)出发后几小时乙船在甲船的正东方向?(结果精确到0.1小时)
(参考数据:
≈1.41,
6.解:(1)设出发后x小时时两船与港口P的距离相等.
根据题意,得81-9x=18x,
解这个方程,得x=3.
∴出发后3小时两船与港口P的距离相等.
在Rt△CEP中,∠CPE=45°,
∴PE=PC·cos45°.
在Rt△PED中,∠EPD=60°,
∴PE=PD·cos60°.
∴(81-9x)·cos45°=18x·cos60°.
解这个方程,得x≈3.7.
∴出发后约3.7小时乙船在甲船的正东方向.
(2)如图,设出发后x小时乙船在甲船的正东方向,此时甲、乙两船的位置分别在点C、D处,连结CD.过点P作PE⊥CD,垂足为E.则点E在点P的正南方向.
1.如图①,一架长4米的梯子AB斜靠在与地面OM垂直的墙ON上,梯子与地面的倾斜角α为60°.(1)求AO与BO的长;(2)若梯子顶端A沿NO下滑,同时底端B沿OM向右滑行.①如图②,设A点下滑到C点,B点向右滑行到D点,并且AC:BD=2:3,试计算梯子顶端A沿NO下滑多少米;②如图③,当A点下滑到A′点,B点向右滑行到B′点时,梯子AB的中点
P也随之运动到
P′点,若
∠POP′=15°,
试求AA′的长.
题型6 中考新题型
① ② ③
2.如果正方形网格中的每一个小正方形边长都是1,则每个小格的顶点叫做格点.
(1)在图①中,以格点为顶点画一个三角形,使三角形的三边长分别为3,
(2)在图②中,线段AB的端点在格点上,请画出以AB为一边的三角形,使这个三角形的面积为6(要求至少画出3个).
(3)在图③中,△MNP的顶点M、N在格点上,P在小正方形的边上,问这个三角形的面积相当于多少个小方格的面积?在你解
出答案后,说说
你的解题方法.
① ② ③
(3)若在(1)的条件下,
S△AMN:S△ABE=9:64,
且线段BF与EF的长是
关于y的一元二次方程
5y2-16ky+10k2+5=0的两个实数根,求BC的长.
3.已知:如图,AD为Rt△ABC斜边BC上的高,点E为DA延长线上一点,连结BE,过点C作CF⊥BE于点F,交AB、AD于M、N两点.
(1)若线段AM、AN的长是关于x的一元二次方程x2-2mx+n2-mn+
m2=0的两个实数根.求证:AM=AN.
(2)若AN=
求DE的长;
复习回顾:
1、什么叫函数?函数有哪三种表示法?
2、三角函数为什么是函数 自变量是什么?因变量呢?
3、三角函数中自变量的取值范围是什么?因变量呢?
4、三角函数间有那些关系?如何证明?
三边之间的关系
a2+b2=c2(勾股定理);
锐角之间的关系
∠A+∠B=90
边角之间的关系(锐角三角函数)
tanA=
a
b
sinA=
a
c
1、
cosA=
b
c
A
C
B
a
b
c
解直角三角形的依据
2、30°,45°,60°的三角函数值
30° 45° 60°
sina
cosa
tana
1
┌
┌
45°
45°
30°
60°
在解直角三角形及应用时经常接触到的一些概念
l
h
α
(2)坡度
tan α =
h
l
概念反馈
(1)仰角和俯角
视线
铅垂线
水平线
视线
仰角
俯角
(3)方位角
30°
45°
B
O
A
东
西
北
南
α为坡角
解直角三角形:(如图)
1.已知a,b.解直角三角形(即求:∠A,∠B及C边)
2. 已知∠A,a.解直角三角形
3.已知∠A,b. 解直角三角形
4. 已知∠A,c. 解直角三角形
b
A
B
C
a
┌
c
只有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角
【热点试题归类】
题型1 三角函数
1. 在Rt△ABC中,∠C=90°,AB=5,AC=4,则sinA的值为_______.
2. 在Rt△ABC中,∠C =90°,BC=4,AC=3,则cosA的值为______.
3. 如图,在△ABC中,∠C =90°,BC=5,AC=12,则cosA等于( )
D
4. 如图,在Rt△ABC中,∠ACB =90°,CD⊥AB于点D,已知AC=
BC=2,那么sin∠ABC=( )
,
A.
A.tan∠AED B.tan∠AEB
C.sin∠AED D.cos∠AED
5. 如图所示,AB是⊙O的直径,弦AC、BD相交于E,则
等于( )
6.计算:
|-
|+(cos60°-tan30°)0+
.
A
D
题型2 解直角三角形
1.如图4,在矩形ABCD中DE⊥AC于E,设∠ADE=a,且cosα=
AB=4,则AD的长为( )
,
A.3 B.
2.2002年8月在北京召开的国际数学家大会会标如图5所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是13,小正方形的面积是1,直角三角形的较长直角边为a,较短直角边为b,
则a +b4的值为( )
A.35 B.43 C.89 D.97
B
B
题型3 解斜三角形
1.如图所示,已知:在△ABC中,∠A=60°,∠B=45°,AB=8,求△ABC的面积(结果可保留根号).
2.如图,海上有一灯塔P,在它周围3海里处有暗礁,一艘客轮以9海里/时的速度由西向东航行,行至A点处测得P在它的北偏东60°的方向,继续行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向,问客轮不改变方向继续前进有无触礁的危险?
1、解:过C作CD⊥AB于D, 设CD=x.在Rt△ACD中,
∵∠A=60°,∴∠ACD=30°.
tan∠ACD =tan30°=
在Rt△BCD中, ∵∠B=45°,∴BD=CD=x.
∴
x+x=8.
解得x=4(3-
).
=16(3-
)=48-16
.
,
∴AD=
x.
AB·CD=
×8×4(3-
∴S△ABC=
)
2.解:过P作PC⊥AB于C点,据题意知:
AB=9×
=3,∠PAB=90°-60°=30°,
∠PBC=90°-45°=45°,∠PCB=90°.
∴PC=BC.
在Rt△APC中,
PC>3.
∴客轮不改变方向继续前进无触礁危险.
tan30°=
,
即
=
,
3.如图,某校九年级3班的一个学生小组进行测量小山高度的实践活动.部分同学在山脚点A测得山腰上一点D的仰角为30°,并测得AD的长度为180米;另一部分同学在山顶点B测得山脚点A的俯角为45°,山腰点D的俯角为60°.请你帮助他们计算出小山的高度BC(计算过程和结果都不取近似值).
在Rt△ADF中,AD=180,∠DAF=30°,
∴DF=90,AF=90
3.解:如图设BC=x,
解得x=90
+90.
(x-90).
FC=AC-AF=x-90
.
∵∠BAC=∠ABC=45°,
∴AC=BC=x.
∴BE=BC-EC=x-90.
在Rt△BDE中,∠BDE=60°,
∴DE=
BE=
.
(x-90)=x-90
∵DE=FC,
∴
.
4.如图,在观测点E测得小山上铁塔顶A的仰角为60°,铁塔底部B的仰角为45°.已知塔高AB=20m,观察点E到地面的距离EF=35m,求小山BD的高(精确到0.1m,
≈1.732).
4.解:如图,过C点作CE⊥AD于C.
x-x.
解得x=10
∵AB=AC-BC,
即20=
∴BD=BC+CD=BC+EF
设BC=x,则EC=BC=x.
在Rt△ACE中,AC=
x,
+10.
+10+35≈45+10×1.732≈62.3(m).
所以小山BD的高为62.3m.
=10
题型4 应用举例
1.有人说,数学家就是不用爬树或把树砍倒就能够知道树高的人.小敏想知道校园内一棵大树的高(如图),她测得CB=10米,∠ACB=50°,请你帮助她算出树高AB约为________米.(注:①树垂直于地面;②供选用数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.2)
12
2.如图,小华为了测量所住楼房的高度,他请来同学帮忙,测量了同一时刻他自己的影长和楼房的影长分别是0.5米和15米,已知小华的身高为1.6米,那么分所住楼房的
高度为________米.
3.如图,两建筑物AB和CD的水平距离为30米,从A点测得D点的俯角为30°,测得C点的俯角为60°,则建筑物CD的高为______米.
48
20
4.如图,花丛中有一路灯杆AB.在灯光下,小明在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时小明的影长GH=5米.如果小明的身高为1.7米,求路灯杆AB的高度(精确到0.1米).
4.解:设AB=x米,BD=y米.
由△CDE∽△ABE得
. ①
由△FGH∽△ABH得
. ②
由①,②得y=7.5,x=5.95≈6.0米.
所以路灯杆AB的高度约为6.0米.
5.如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点.已知∠BAC=65°,∠DAE=45°,点D到地面的垂直距离DE=3 m,求点B到地面的垂直距离BC(精确到0.1m).
5.解:在Rt△ADE中,DE=3
∠DAE=45°,
∴sin∠DAE=
∴AD=6.
又∵AD=AB,
在Rt△ABC中,sin∠BAC=
∴BC=AB·sin∠BAC=6·sin65°≈5.4.
答:点B到地面的垂直距离BC约为5.4米.
,
,
,
6.如图,我市某广场一灯柱AB被一钢缆CD固定,CD与地面成40°夹角,且DB=5m,现要在C点上方2m处加固另一条钢缆ED,那么EB的高为多少米?(结果保留三个有效数字)
6.解:在Rt△BCD中,∠BDC=40°,DB=5m,
∵tan∠BDC=
∴BC=DB·tan∠BDC
=5×tan40°≈4.195.
∴EB=BC+CE=4.195+2≈6.20.
答:略.
,
7.如图,在电线杆上的C处引位线CE、CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B处安置测角仪,在A处测得电线杆C处的仰角为30°,已知测角仪AB高为1.5米,求拉线CE的长.(结果保留根号)
7.解:过点A作AH⊥CD,垂足为H.
由题意可知四边形ABDH为矩形,
∠CAH=30°,
∴AB=DH=1.5,BD=AH=6.
在Rt△ACH中,tan∠CAH=
,
∴CH=AH·tan∠CAH=6tan30°=6×
=2
在Rt△CDE中 ,
∵∠CED=60°,sin∠CED=
∴CE=
=(4+
)(米).
∵DH=1.5,∴CD=2
+1.5.
答:拉线CE的长为(4+
)米.
8.已知:如图,在山脚的C处测得山顶A的仰角为45°,沿着坡度为30°的斜坡前进400米到D处(即∠DCB=30°,CD=400米),测得A的仰角为60°,求山的高度AB.
9.如图,在一个坡角为15°的斜坡上有一棵树,高为AB.当太阳光与水平线成50°时,测得该树在斜坡的树影BC的长为7m,求树高.(精确到0.1m)
在矩形DEBF中,BE=DF=200米,
在Rt△ACB中,∠ACB=45°,
∴AB=BC,
即
8.解:如图,作DE⊥AB于E,作DF⊥BC于F,在Rt△CDF中∠DCF=30°,CD=400米,
∴DF=CD·sin30°=
×400=200(米).
CF=CD·cos30°=
×400=200 (米).
+x.
x+200=200
∴x=200,
∴AB=AE+BE=(200
+200)米.
在Rt△ADE中,∠ADE=60°,设DE=x米,
∴AE=tan60°·x=
x(米).
∵∠BCD=15°,
∴∠ACD=50°,
在Rt△CDB中,
CD=7×cos15°,
BD=7×sin15°.
在Rt△CDA中,
AD=CD×tan50°=7×cos15°×tan50°.
∴AB=AD-BD
=(7×cos15°×tan50°-7×sin15°)
=7(cos15°×tan50°-sin15°)≈6.2(m).
答:树高约为6.2m.
9.解:如图,过点C作水平线与AB的延长线交于点D,则AD⊥CD.
这节课你有哪些收获
你能否用所学的知识去解决一些
实际问题吗
题型5 综合与创新
1.小明骑自行车以15千米/小时的速度在公路上向正北方向匀速行进,如图1,出发时,在B点他观察到仓库A在他的北偏东30°处,骑行20分钟后到达C点,发现此时这座仓库正好在他的东南方向,则这座仓库到公路的距离为_____千米.(参考数据:
≈1.732,结果
保留两位有效数字)
1.8
2.先将一矩形ABCD置于直角坐标系中,使点A与坐标系的原点重合,边AB、AD分别落在x轴、y轴上(如左图),再将此矩形在坐标平面内按逆时针方向绕原点旋转30°(如右图),若AB=4,BC=3 ,则左图和右图中点B的坐标为___,点C的坐标为____.
答案:图(2)中:B(4,0),图(3)中:B(2 ,2);
图(2)中:C(4,3),图(3)中:C(
).
3.数学活动课上,小敏、小颖分别画了△ABC和△DEF,数据如图,如果把小敏画的三角形面积记作S△ABC,小颖画的三角形面积记作S△DEF,那么你认为( )
A.S△ABC >S△DEF B.S△ABC
小敏画的三角形 小颖画的三角形
C
4.已知:如图,在△ABC中,AD是边BC上的高,E为边AC的中点,BC= 14,AD=12,sinB=
求:(1)线段DC的长;
(2)tan∠EDC的值.
∴CD=BC-BD=14-9=5.
(2)∵E是Rt△ADC斜边AC的中点,
∴DE=EC,∴∠EDC=∠C.
∴tan∠EDC=tan∠C=
.
4.解:(1)在Rt△ABD中,AB=
=15.
∴BD=
=9.
5.某校教学楼后面紧邻着一个土坡,坡上面是一块平地,如图所示,BC∥AD,斜坡AB长22m,坡角∠BAD=68°,为了防止山体滑坡,保障安全,学校决定对该土坡进行改造.经地质人员勘测,当坡角不超过50°时,可确保山体不滑坡.(1)求改造前坡顶与地面的距离BE的长(精确到0.1m);(2)为确保安全,学校计划改造时保持坡脚A不动,坡顶B沿BC削进到F点处,问BF至少是多少米(精确到0.1m)?
(参考数据:sin68°≈0.927 2,
cos68°≈0.374 6,tan68°≈2.475 1,
tan50°≈0.766 0,cos50°≈0.642 8,
tan50°≈1.191 8)
5.解:如图,(1)作BE⊥AD,E为垂足.
AE=AB·cos68°
=22cos68°≈8.24,
∴BF=AG-AE=8.88
≈8.9 (m).
即BF至少是8.9m.
则BE=AB·sin68°=22sin68°≈20.40=20.4(m)(2)作FG⊥AD,G为垂足,
连结FA,则FG=BE.
∵AG=
=17.12,
≈1.73)
6.如图,小岛A在港口P的南偏西45°方向,距离港口81海里处.甲船从A出发,沿AP方向以9海里/时的速度驶向港口,乙船从港口P出发,沿南偏东60°方向,以18海里/时的速度驶离港口,现两船同时出发,
(1)出发后几小时两船与港口P的距离相等?
(2)出发后几小时乙船在甲船的正东方向?(结果精确到0.1小时)
(参考数据:
≈1.41,
6.解:(1)设出发后x小时时两船与港口P的距离相等.
根据题意,得81-9x=18x,
解这个方程,得x=3.
∴出发后3小时两船与港口P的距离相等.
在Rt△CEP中,∠CPE=45°,
∴PE=PC·cos45°.
在Rt△PED中,∠EPD=60°,
∴PE=PD·cos60°.
∴(81-9x)·cos45°=18x·cos60°.
解这个方程,得x≈3.7.
∴出发后约3.7小时乙船在甲船的正东方向.
(2)如图,设出发后x小时乙船在甲船的正东方向,此时甲、乙两船的位置分别在点C、D处,连结CD.过点P作PE⊥CD,垂足为E.则点E在点P的正南方向.
1.如图①,一架长4米的梯子AB斜靠在与地面OM垂直的墙ON上,梯子与地面的倾斜角α为60°.(1)求AO与BO的长;(2)若梯子顶端A沿NO下滑,同时底端B沿OM向右滑行.①如图②,设A点下滑到C点,B点向右滑行到D点,并且AC:BD=2:3,试计算梯子顶端A沿NO下滑多少米;②如图③,当A点下滑到A′点,B点向右滑行到B′点时,梯子AB的中点
P也随之运动到
P′点,若
∠POP′=15°,
试求AA′的长.
题型6 中考新题型
① ② ③
2.如果正方形网格中的每一个小正方形边长都是1,则每个小格的顶点叫做格点.
(1)在图①中,以格点为顶点画一个三角形,使三角形的三边长分别为3,
(2)在图②中,线段AB的端点在格点上,请画出以AB为一边的三角形,使这个三角形的面积为6(要求至少画出3个).
(3)在图③中,△MNP的顶点M、N在格点上,P在小正方形的边上,问这个三角形的面积相当于多少个小方格的面积?在你解
出答案后,说说
你的解题方法.
① ② ③
(3)若在(1)的条件下,
S△AMN:S△ABE=9:64,
且线段BF与EF的长是
关于y的一元二次方程
5y2-16ky+10k2+5=0的两个实数根,求BC的长.
3.已知:如图,AD为Rt△ABC斜边BC上的高,点E为DA延长线上一点,连结BE,过点C作CF⊥BE于点F,交AB、AD于M、N两点.
(1)若线段AM、AN的长是关于x的一元二次方程x2-2mx+n2-mn+
m2=0的两个实数根.求证:AM=AN.
(2)若AN=
求DE的长;
