8.3 实际问题与二元一次方程组 课件(共25张PPT)
文档属性
| 名称 | 8.3 实际问题与二元一次方程组 课件(共25张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 720.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-23 00:00:00 | ||
图片预览







文档简介
(共25张PPT)
8.3 实际问题与二元一次方程组
第八章 二元一次方程组
七年级数学下册同步(人教版)
1.用二元一次方程组解决实际问题.
2.体会数学建模的思想.
重点:理解题意,寻求题中等量关系列方程.
难点:寻找“关键词”,列出等量关系.
学习目标
列方程组解应用题的步骤:
1. 审题
2. 设未知数
3. 列二元一次方程组
4. 解二元一次方程组
5 .检验
6. 答
回顾旧知
养牛场原有30只大牛和15只小牛,1天约需要饲料675kg克;一周后又购进12只大牛和5只小牛,这时1天约需要饲料940kg。饲养员李大叔估计平均每只大牛1天约需饲料18至20kg,每只小牛1天约需要饲料7至8kg。请你通过计算检验李大叔的估计是否正确?
1、怎样检验他的估计呢?
2、题目中包含怎样的等量关系?
探究新知
怎样判断李大叔的估计是否正确?
求出每头大牛和每头小牛一天各自大约需用饲料量
(1)30头大牛和15头小牛1天需用饲料675kg;
(2)42头大牛和20头小牛1天需用饲料940kg;
每头大牛和每头小牛一天各自大约需用饲料量
题目中有哪些未知量?
题目中有哪些等量关系?
(3)12头大牛和5头小牛1天需用饲料940kg—675kg;
探究新知
大牛所吃饲料 小牛所 吃饲料 合计
以前所用饲料
后来所用饲料
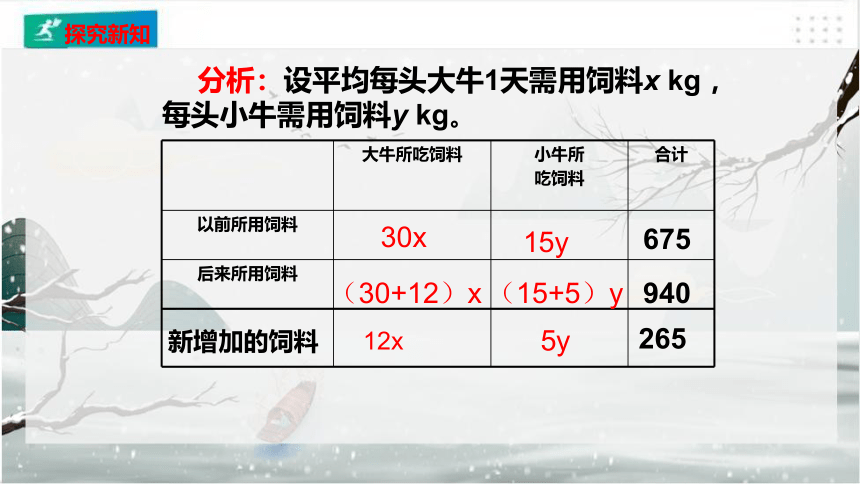
分析:设平均每头大牛1天需用饲料x kg ,每头小牛需用饲料y kg。
30x
(30+12)x
15y
(15+5)y
675
940
新增加的饲料
12x
5y
265
探究新知
解:设平均每头大牛和每头小牛各约需饲料xkg和ykg.
根据题意,列方程组:
解这个方程组,得:
这就是说,平均每头大牛1天约需饲料20kg,每头小牛1天约需饲料5kg。饲养员李大叔对大牛的食量估计较准确,对小牛的食量估计偏高。
化简,得
探究新知
长18米的钢材,要锯成10段,而每段的长只能取“1米或2米”两种型号之一,小明估计2米的有3段,你们认为他估计的是否准确?为什么呢?那2米和1米的各应取多少段?
探究新知
解:设应取2米的x段,1米的y段,则
答:小明估计不准确。2米的应取8段,1米的应取2段。
解得:
依题意得
探究新知
长青化工厂用汽车从A地购买一批原料运回工厂,
制成产品后用火车运到B地。工厂与A地相距80千米,
与B地相距150千米。公路运价为1.5元/(吨·千米),
铁路运价为1.2元/(吨·千米),这两次运输支出公路运费
15000元,铁路运费97200元。求工厂从A地购得的原料
有多少吨?制成的产品有多少吨?
分析:题中的量很多,并且相互关联,这时,我们可画一张示意图,把题中的条件在图中标出来,这样比较直,能帮助我们比较顺利地找出题中的相等关系。
探究新知
A地
B地
长青化工厂
公路80km
铁路150km
原料
产品
1.5元/(吨·千米)
1.2元/(吨·千米)
公路运费:15000元 铁路运费:97200元
长青化工厂用汽车从A地购买一批原料运回工厂,制成产品后用火车运到B地。工厂与A地相距80千米,与B地相距150千米。公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输支出公路运费15000元,铁路运费97200元。求工厂从A地购得的原料有多少吨?制成的产品有多少吨?
探究新知
长青化工厂用汽车从A地购买一批原料运回工厂,制成产品后用火车运到B地。工厂与A地相距80千米,与B地相距150千米。公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),
这两次运输支出公路运费15000元,铁路运费97200元。求工厂从A地购得的原料有多少吨?制成的产品有多少吨?
解:制成的产品为x 吨,设购得的原料为y吨,
根据题意得
{
1.5 × 80 ×y =15000
1.2×150 ×x =97200
解得:
{
x=540
y=125
答:购得的原料为125吨, 制成的产品为540 吨。
画示意图是解决道路运输问题的手段之一。
合作探究
探究 如图,长青化工厂与A,B两地有公路、铁路相连.这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运到B地. 公路运价为1.5元/(t·km),铁路运价为1.2元/(t·km),这两次运输共支出公路运费15 000元,铁路运费97 200元.这批产品的销售款比原料费与运输费的和多多少元?
合作探究
问题1 公路运价为1. 5元/(t·km),铁路运价为1.2元/(t·km)是什
么意思?
如:把2吨货物从A地运到100千米外的B地,
经公路运输需要支付:
公路运价:经公路运输1吨货物行驶1千米需1.5元
铁路运价:经铁路运输1吨货物行驶1千米需1.2元
1.5×2×100=300元,
1.2×2×100=240元
运输费 = 运价 × 质量 × 路程
经铁路运输需要支付:
合作探究
问题2 两次运输共支出公路运费15000元指的是什么?
原料的公路运费+产品的公路运费=15000
问题3 两次运输共支出铁路运费97200元指的又是什么?
原料的铁路运费+产品的铁路运费=97200
合作探究
问题4 这道题求的是什么?
这批产品的销售款比原料费与运输费的和多多少元?
问题5 要解决这个问题我们必须先知道什么?
销售款 原料费 运输费
销售款=产品单价×产品数量
原料费=原料单价×原料数量
运输费=铁路运费+公路运费
合作探究
设产品为x吨,原料为y吨。
1.2·y ·120
1.5·y·10
1.5·x ·20
1.2·x ·110
运输费 = 运价 × 质量 × 路程
产品x吨 原料y吨 合计
公路运费(元)
铁路运费(元)
价值(元)
1.5×20x
1.5×10y
15000
1.2×110x
1.2×120y
97200
8000x
1000y
设产品为 x 吨,原料为 y 吨。
解:设产品为x吨,原料为y吨,由题意得
解得:
销售款为:
8000×300=2400000(元)
原料费为:
1000×400=400000(元)
运输费为:
15000+97200=112200(元)
2400000-(400000+112200)=1887800(元)
答:销售款比原料费与运输费的和多1887800元。
一艘轮船顺流航行45千米需要3小时,逆流航行65千米需要5小时,求船在静水中的速度和水流速度。
解:设船在静水中的速度为x千米/时,水流的速度为y千米/时,根据题意,得
答:船在静水中的速度及水流的速度分别为14千米/时、1千米/时.
解这个方程组得,
即
合作探究
用方程组解决实际问题有哪些步骤?
(1)设未知数,一般求什么就设什么
(2)找两个等量关系
(3)列方程组
(4)解方程组
(5)检验并做答
总结归纳
解决实际问题的基本过程
实际问题
设未知数、列方程(组)
数学问题
二元一次方程组
解方程
(组)
数学问题的解
二元一次方程组的解
检 验
实际问题的答案
建模
课堂小结
1、某工人原计划在限定时间内加工一批零件.如果每小时加工10个零件,就可以超额完成3 个;如果每小时加工11个零件就可以提前1h完成.问这批零件有多少个 按原计划需多少小时 完成
解:设这批零件有x个,按原计划需y小时完成,根据题意得
解这个方程组得,
答:这批零件有77个,按原计划需8小时完成。
当堂检测
2.一个长方形的周长是200 cm,长比宽的3倍少4 cm,求长和宽各是多少.
3.A市至B市的航线长9750千米,一架飞机从A市飞往B市需12.5小时,它逆风飞行同样的航线需13小时.求飞机的平均速度以及风速.
当堂检测
https://www.21cnjy.com/help/help_extract.php
8.3 实际问题与二元一次方程组
第八章 二元一次方程组
七年级数学下册同步(人教版)
1.用二元一次方程组解决实际问题.
2.体会数学建模的思想.
重点:理解题意,寻求题中等量关系列方程.
难点:寻找“关键词”,列出等量关系.
学习目标
列方程组解应用题的步骤:
1. 审题
2. 设未知数
3. 列二元一次方程组
4. 解二元一次方程组
5 .检验
6. 答
回顾旧知
养牛场原有30只大牛和15只小牛,1天约需要饲料675kg克;一周后又购进12只大牛和5只小牛,这时1天约需要饲料940kg。饲养员李大叔估计平均每只大牛1天约需饲料18至20kg,每只小牛1天约需要饲料7至8kg。请你通过计算检验李大叔的估计是否正确?
1、怎样检验他的估计呢?
2、题目中包含怎样的等量关系?
探究新知
怎样判断李大叔的估计是否正确?
求出每头大牛和每头小牛一天各自大约需用饲料量
(1)30头大牛和15头小牛1天需用饲料675kg;
(2)42头大牛和20头小牛1天需用饲料940kg;
每头大牛和每头小牛一天各自大约需用饲料量
题目中有哪些未知量?
题目中有哪些等量关系?
(3)12头大牛和5头小牛1天需用饲料940kg—675kg;
探究新知
大牛所吃饲料 小牛所 吃饲料 合计
以前所用饲料
后来所用饲料
分析:设平均每头大牛1天需用饲料x kg ,每头小牛需用饲料y kg。
30x
(30+12)x
15y
(15+5)y
675
940
新增加的饲料
12x
5y
265
探究新知
解:设平均每头大牛和每头小牛各约需饲料xkg和ykg.
根据题意,列方程组:
解这个方程组,得:
这就是说,平均每头大牛1天约需饲料20kg,每头小牛1天约需饲料5kg。饲养员李大叔对大牛的食量估计较准确,对小牛的食量估计偏高。
化简,得
探究新知
长18米的钢材,要锯成10段,而每段的长只能取“1米或2米”两种型号之一,小明估计2米的有3段,你们认为他估计的是否准确?为什么呢?那2米和1米的各应取多少段?
探究新知
解:设应取2米的x段,1米的y段,则
答:小明估计不准确。2米的应取8段,1米的应取2段。
解得:
依题意得
探究新知
长青化工厂用汽车从A地购买一批原料运回工厂,
制成产品后用火车运到B地。工厂与A地相距80千米,
与B地相距150千米。公路运价为1.5元/(吨·千米),
铁路运价为1.2元/(吨·千米),这两次运输支出公路运费
15000元,铁路运费97200元。求工厂从A地购得的原料
有多少吨?制成的产品有多少吨?
分析:题中的量很多,并且相互关联,这时,我们可画一张示意图,把题中的条件在图中标出来,这样比较直,能帮助我们比较顺利地找出题中的相等关系。
探究新知
A地
B地
长青化工厂
公路80km
铁路150km
原料
产品
1.5元/(吨·千米)
1.2元/(吨·千米)
公路运费:15000元 铁路运费:97200元
长青化工厂用汽车从A地购买一批原料运回工厂,制成产品后用火车运到B地。工厂与A地相距80千米,与B地相距150千米。公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输支出公路运费15000元,铁路运费97200元。求工厂从A地购得的原料有多少吨?制成的产品有多少吨?
探究新知
长青化工厂用汽车从A地购买一批原料运回工厂,制成产品后用火车运到B地。工厂与A地相距80千米,与B地相距150千米。公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),
这两次运输支出公路运费15000元,铁路运费97200元。求工厂从A地购得的原料有多少吨?制成的产品有多少吨?
解:制成的产品为x 吨,设购得的原料为y吨,
根据题意得
{
1.5 × 80 ×y =15000
1.2×150 ×x =97200
解得:
{
x=540
y=125
答:购得的原料为125吨, 制成的产品为540 吨。
画示意图是解决道路运输问题的手段之一。
合作探究
探究 如图,长青化工厂与A,B两地有公路、铁路相连.这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运到B地. 公路运价为1.5元/(t·km),铁路运价为1.2元/(t·km),这两次运输共支出公路运费15 000元,铁路运费97 200元.这批产品的销售款比原料费与运输费的和多多少元?
合作探究
问题1 公路运价为1. 5元/(t·km),铁路运价为1.2元/(t·km)是什
么意思?
如:把2吨货物从A地运到100千米外的B地,
经公路运输需要支付:
公路运价:经公路运输1吨货物行驶1千米需1.5元
铁路运价:经铁路运输1吨货物行驶1千米需1.2元
1.5×2×100=300元,
1.2×2×100=240元
运输费 = 运价 × 质量 × 路程
经铁路运输需要支付:
合作探究
问题2 两次运输共支出公路运费15000元指的是什么?
原料的公路运费+产品的公路运费=15000
问题3 两次运输共支出铁路运费97200元指的又是什么?
原料的铁路运费+产品的铁路运费=97200
合作探究
问题4 这道题求的是什么?
这批产品的销售款比原料费与运输费的和多多少元?
问题5 要解决这个问题我们必须先知道什么?
销售款 原料费 运输费
销售款=产品单价×产品数量
原料费=原料单价×原料数量
运输费=铁路运费+公路运费
合作探究
设产品为x吨,原料为y吨。
1.2·y ·120
1.5·y·10
1.5·x ·20
1.2·x ·110
运输费 = 运价 × 质量 × 路程
产品x吨 原料y吨 合计
公路运费(元)
铁路运费(元)
价值(元)
1.5×20x
1.5×10y
15000
1.2×110x
1.2×120y
97200
8000x
1000y
设产品为 x 吨,原料为 y 吨。
解:设产品为x吨,原料为y吨,由题意得
解得:
销售款为:
8000×300=2400000(元)
原料费为:
1000×400=400000(元)
运输费为:
15000+97200=112200(元)
2400000-(400000+112200)=1887800(元)
答:销售款比原料费与运输费的和多1887800元。
一艘轮船顺流航行45千米需要3小时,逆流航行65千米需要5小时,求船在静水中的速度和水流速度。
解:设船在静水中的速度为x千米/时,水流的速度为y千米/时,根据题意,得
答:船在静水中的速度及水流的速度分别为14千米/时、1千米/时.
解这个方程组得,
即
合作探究
用方程组解决实际问题有哪些步骤?
(1)设未知数,一般求什么就设什么
(2)找两个等量关系
(3)列方程组
(4)解方程组
(5)检验并做答
总结归纳
解决实际问题的基本过程
实际问题
设未知数、列方程(组)
数学问题
二元一次方程组
解方程
(组)
数学问题的解
二元一次方程组的解
检 验
实际问题的答案
建模
课堂小结
1、某工人原计划在限定时间内加工一批零件.如果每小时加工10个零件,就可以超额完成3 个;如果每小时加工11个零件就可以提前1h完成.问这批零件有多少个 按原计划需多少小时 完成
解:设这批零件有x个,按原计划需y小时完成,根据题意得
解这个方程组得,
答:这批零件有77个,按原计划需8小时完成。
当堂检测
2.一个长方形的周长是200 cm,长比宽的3倍少4 cm,求长和宽各是多少.
3.A市至B市的航线长9750千米,一架飞机从A市飞往B市需12.5小时,它逆风飞行同样的航线需13小时.求飞机的平均速度以及风速.
当堂检测
https://www.21cnjy.com/help/help_extract.php
