6.3.2 刻画空间点、线、面位置关系的公理 教案
文档属性
| 名称 | 6.3.2 刻画空间点、线、面位置关系的公理 教案 |
|
|
| 格式 | docx | ||
| 文件大小 | 187.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-23 20:05:09 | ||
图片预览





文档简介
刻画空间点、线、面位置关系的公理
【第一课时】
【教学目标】
掌握空间图形的基本事实1、2、3.
【教学重难点】
掌握平面的基本事实及推论.
【教学过程】
一、基础铺垫
平面的基本事实及推论:
公理 内容 图形 符号
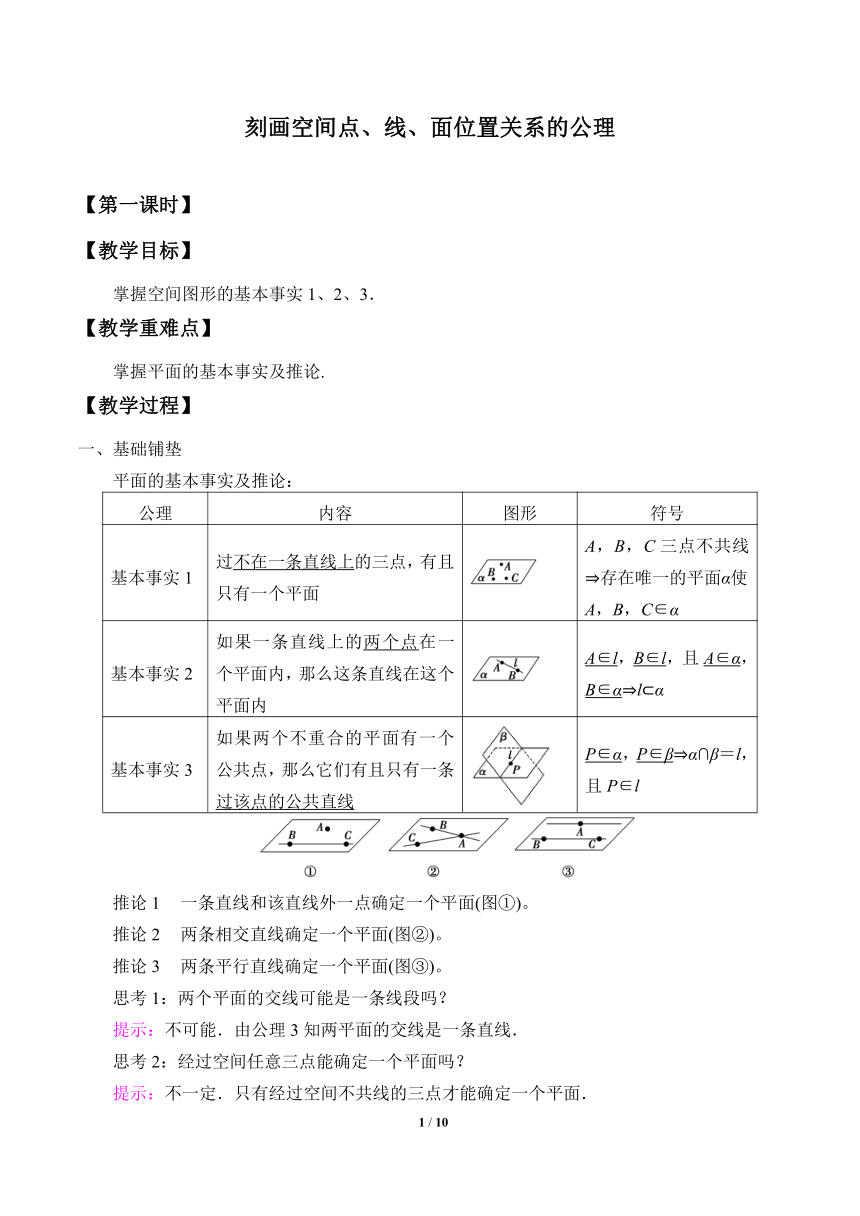
基本事实1 过不在一条直线上的三点,有且只有一个平面 A,B,C三点不共线 存在唯一的平面α使A,B,C∈α
基本事实2 如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内 A∈l,B∈l,且A∈α,B∈α l α
基本事实3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线 P∈α,P∈β α∩β=l,且P∈l
推论1 一条直线和该直线外一点确定一个平面(图①)。
推论2 两条相交直线确定一个平面(图②)。
推论3 两条平行直线确定一个平面(图③)。
思考1:两个平面的交线可能是一条线段吗?
提示:不可能.由公理3知两平面的交线是一条直线.
思考2:经过空间任意三点能确定一个平面吗?
提示:不一定.只有经过空间不共线的三点才能确定一个平面.
二、合作探究
1.点线共面问题
【例1】 证明:两两相交且不共点的三条直线在同一平面内.
[思路探究] 先说明两条相交直线确定一个平面,然后证明另外一条直线也在该平面内.或利用公理1的推论,说明三条相交直线分别确定两个平面α,β,然后证明α,β重合.
[解] 已知:如图所示,l1∩l2=A,l2∩l3=B,l1∩l3=C.
求证:直线l1,l2,l3在同一平面内.
法一:∵l1∩l2=A,∴l1和l2确定一个平面α.
∵l2∩l3=B,∴B∈l2又l2α,∴B∈α.
同理可证C∈α,又B∈l3,C∈l3,∴l3α.
∴直线l1,l2,l3在同一平面内.
法二:∵l1∩l2=A,∴l1,l2确定一个平面α.
∵l2∩l3=B,∴l2,l3确定一个平面β.
∵A∈l2,l2α,∴A∈α.
∵A∈l2,l2β,∴A∈β.
同理可证,B∈α,B∈β,C∈α,C∈β.
∵不共线的三个点A,B,C既在平面α内,又在平面β内,
∴平面α和平面β重合,即直线l1,l2,l3在同一平面内.
【规律方法】
证明点、线共面问题的理论依据是公理1和公理2,常用方法有:
(1)先由部分点、线确定一个面,再证其余的点、线都在这个平面内,即用“纳入法”;
(2)先由其中一部分点、线确定一个平面α,其余点、线确定另一个平面β,再证平面α与β重合,即用“同一法”;
(3)假设不共面,结合题设推出矛盾,即用“反证法”.
2.点共线与线共点问题
[探究问题]
(1)如图所示,在空间四边形各边AD,AB,BC,CD上分别取E,F,G,H四点,如果EF,GH交于一点P,那么点P,B,D共线吗?请说明理由.
提示:连接BD(图略).
∵EF,HG相交于一点P,
且EF平面ABD,GH平面CBD,
∴P∈平面ABD且P∈平面CBD.
又平面ABD∩平面BCD=BD,
∴P∈BD,∴点P,B,D共线.
(2)如图,在正方体ABCD A1B1C1D1中,设线段A1C与平面ABC1D1交于点Q,能否判断B,Q,D1三点共线?
提示:∵D1∈平面ABC1D1,D1∈平面A1D1CB,B∈平面ABC1D1,B∈平面A1D1CB,
∴平面ABC1D1∩平面A1D1CB=BD1.
∵A1C∩平面ABC1D1=Q,且A1C平面A1D1CB,
∴Q∈平面A1D1CB,Q∈平面ABC1D1,
∴Q在两平面的交线BD1上,∴B,Q,D1三点共线.
【例2】 已知△ABC在平面α外,它的三边所在的直线分别交平面α于P,Q,R(如图).求证:P,Q,R三点共线.
[思路探究] 解答本题可以先选两点确定一条直线,再证明第三点也在这条直线上.
[证明] 法一:∵AB∩α=P,∴P∈AB,P∈平面α.
又AB平面ABC,∴P∈平面ABC.
∴由公理3可知,点P在平面ABC与平面α的交线上.
同理可证Q,R也在平面ABC与平面α的交线上.
∴P,Q,R三点共线.
法二:∵AP∩AR=A,
∴直线AP与直线AR确定平面APR.
又∵AB∩α=P,AC∩α=R,
∴平面APR∩平面α=PR.
∵B∈平面APR,C∈平面APR,
∴BC平面APR.又∵Q∈直线BC,
∴Q∈平面APR.又Q∈α,
∴Q∈PR,∴P,Q,R三点共线.
【规律方法】
1.证明多点共线主要采用如下两种方法:一是首先确定两个平面,然后证明这些点是这两个平面的公共点,再根据公理3,这些点都在这两个平面的交线上;二是选择其中两点确定一条直线,然后再证明其他的点都在这条直线上.
2.证明三线共点问题的方法主要是:先确定两条直线交于一点,再证明该点是这两条直线所在平面的公共点,第三条直线是这两个平面的交线.
三、课堂小结
1.解决立体几何问题首先应过好三大语言关,即实现这三种语言的相互转换,正确理解集合符号所表示的几何图形的实际意义,恰当地用符号语言描述图形语言,将图形语言用文字语言描述出来,再转换为符号语言.文字语言和符号语言在转换的时候,要注意符号语言所代表的含义,作直观图时,要注意线的实虚.
2.在处理点线共面、三点共线及三线共点问题时初步体会三个公理的作用,突出先部分再整体的思想.
四、课堂检测
1.思考辨析
(1)不平行的两条直线的位置关系为相交. ( )
(2)两个平面的交线可以是一条线段. ( )
(3)直线l在平面α内,可以表示为“lα”. ( )
(4)平面内的直线与不在该平面内的直线互为异面直线. ( )
[解析] (1)×,不平行的两条直线的位置关系为相交或异面,故(1)错.
(2)×,两个平面的交线是直线,故(2)错.
(3)√,正确.
(4)×,可能相交或平行,故(4)错.
[答案] (1)× (2)× (3)√ (4)×
2.设平面α与平面β交于直线l,A∈α,B∈α,且直线AB∩l=C,则直线AB∩β=________.
C [∵α∩β=l,AB∩l=C,∴C∈β,C∈AB,∴AB∩β=C.]
3.若a,b是异面直线,b,c是异面直线,则直线a与直线c的位置关系是________.
平行、相交或异面 [两条直线a,c都与同一条直线b是异面直线,则这两条直线平行、相交或异面都有可能.]
4.已知直线a∥b,直线l与a,b都相交,求证:过a,b,l有且只有一个平面.
[解] 如图所示.∵a∥b,
∴直线a,b确定一个平面,设这个平面为α.
设a∩l=A,b∩l=B,∴A∈α,B∈α,且A∈l,B∈l,
∴lα.即过a,b,l有且只有一个平面.
【第二课时】
【教学目标】
1.掌握基本事实4和“等角定理”.
2.理解异面直线所成的角及直线与直线垂直的定义.
3.会求异面直线所成的角.
【教学重难点】
理解异面直线所成的角及直线与直线垂直的定义.
【教学过程】
一、基础铺垫
1.基本事实4
(1)条件:两条直线平行于同一条直线.
(2)结论:这两条直线平行.
(3)符号表述:.
2.等角定理
(1)条件:空间中,如果两个角的两条边分别对应平行.
(2)结论:这两个角相等或互补.
思考1:当一个角的两边与另一个角的两边分别平行时,试问这两个角在什么情况下相等,在什么情况下互补?
提示:当两个角的两边分别平行且方向相同或相反时,这两个角相等;当两个角的一组边的方向相同,而另一组边的方向相反时,这两个角互补.
3.空间两条直线的位置关系
共面直线
异面直线:不共面的两条直线且没有公共点.
4.异面直线所成的角
定义 过空间任意一点P分别引两条异面直线a,b的平行线l1,l2(a∥l1,b∥l2),这两条相交直线所成的锐角(或直角)就是异面直线a,b所成的角
取值 范围 异面直线所成的角θ的取值范围:
特例 当θ=时,a与b互相垂直,记作a⊥b
思考2:分别在两个平面内的两条直线一定是异面直线吗?
提示:不一定.可能是相交,平行或异面.
二、合作探究
1.基本事实4的应用
【例1】 如图,已知E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点.
(1)求证:四边形EFGH是平行四边形;
(2)若四边形EFGH是矩形,求证:AC⊥BD.
[解] (1)如题图,在△ABD中,
∵EH是△ABD的中位线,
∴EH∥BD,EH=BD.
又FG是△CBD的中位线,
∴FG∥BD,FG=BD,
∴FG∥EH,∴E,F,G,H四点共面,又FG=EH,
∴四边形EFGH是平行四边形.
(2)由(1)知EH∥BD,同理AC∥GH.又∵四边形EFGH是矩形,∴EH⊥GH,∴AC⊥BD.
【规律方法】
空间中证明两直线平行的方法:
(1)借助平面几何知识证明,如三角形中位线性质、平行四边形的性质、用成比例线段证平行等.
(2)利用公理4证明,即证明两直线都与第三条直线平行.
2.等角定理的应用
【例2】 如图,在正方体ABCD A1B1C1D1中,M,M1分别是棱AD和A1D1的中点.
(1)求证:四边形BB1M1M为平行四边形;
(2)求证:∠BMC=∠B1M1C1.
[解] (1)∵ABCD A1B1C1D1为正方体,
∴ADA1D1,
又M,M1分别为棱AD,A1D1的中点,
∴AMA1M1,
∴四边形AMM1A1为平行四边形,
∴MM1AA1.
又AA1=BB1且AA1∥BB1,
∴MM1BB1,
∴四边形BB1M1M为平行四边形.
(2)法一:由(1)知四边形BB1M1M为平行四边形,
∴B1M1∥BM.
同理可得四边形CC1M1M为平行四边形,
∴C1M1∥CM.
由平面几何知识可知,∠BMC和∠B1M1C1都是锐角,
∴∠BMC=∠B1M1C1.
法二:由(1)知四边形BB1M1M为平行四边形,
∴B1M1=BM.
同理可得四边形CC1M1M为平行四边形,
∴C1M1=CM.
又∵B1C1=BC,∴△BCM≌△B1C1M1,
∴∠BMC=∠B1M1C1.
【规律方法】
空间等角定理实质上是由以下两个结论组成的:
(1)若一个角的两边与另一个角的两边分别对应平行且方向都相同或相反,那么这两个角相等;
(2)若一个角的两边与另一个角的两边分别平行,有一组对边方向相同,另一组对边方向相反,那么这两个角互补.
3.求异面直线所成的角
[探究问题]
(1)已知直线a,b是两条异面直线,如何作出这两条异面直线所成的角?
提示:如图,在空间中任取一点O,作直线a′∥a,b′∥b,则两条相交直线a′,b′所成的锐角或直角θ即两条异面直线a,b所成的角.
(2)a′与b′所成角的大小与什么有关,与点O的位置有关吗?通常点O取在什么位置?
提示:a′与b′所成角的大小只由a,b的相互位置确定,与点O的选择无关,一般情况下为了简便,点O选取在两条直线中的一条直线上.
【例3】 如图,在空间四边形ABCD中,AD=BC=2,E,F分别是AB,CD的中点,若EF=,求异面直线AD,BC所成角的大小.
[思路探究] 根据求异面直线所成角的方法,将异面直线AD,BC平移到同一平面内解决.
[解] 如图,取BD的中点M,连接EM,FM.
因为E,F分别是AB,CD的中点,
所以EMAD,FMBC,
则∠EMF或其补角就是异面直线AD,BC所成的角.
因为AD=BC=2,所以EM=MF=1,
在等腰△MEF中,过点M,作MH⊥EF于H,
在Rt△MHE中,EM=1,EH=EF=,
则sin∠EMH=,于是∠EMH=60°,
则∠EMF=2∠EMH=120°.
所以异面直线AD,BC所成的角为∠EMF的补角,
即异面直线AD,BC所成的角为60°.
【规律方法】求两条异面直线所成的角的一般步骤:
(1)构造:根据异面直线的定义,用平移法 常用三角形中位线、平行四边形性质等 作出异面直线所成的角.
(2)证明:证明作出的角就是要求的角.
(3)计算:求角度,常放在三角形内求解.
(4)结论:若求出的角是锐角或直角,则它就是所求异面直线所成的角;若求出的角是钝角,则它的补角就是所求异面直线所成的角.
三、课堂总结
1.判定两直线的位置关系的依据就在于两直线平行、相交、异面的定义.很多情况下,定义就是一种常用的判定方法.
2.在研究异面直线所成角的大小时,通常把两条异面直线所成的角转化为两条相交直线所成的角.将空间问题向平面问题转化,这是我们学习立体几何的一条重要的思维途径.需要强调的是,两条异面直线所成角的范围为(0°,90°],解题时经常结合这一点去求异面直线所成角的大小.
四、课堂练习
1.思考辨析
(1)已知a,b,c,d是四条直线,若a∥b,b∥c,c∥d,则a∥d.
( )
(2)两条直线a,b没有公共点,那么a与b是异面直线. ( )
(3)若a,b是两条直线,α,β是两个平面,且aα,bβ,则a,b是异面直线. ( )
[解析] (2)×,也可能平行.
(3)×,可能平行、相交、异面.
[答案] (1)√ (2)× (3)×
2.下列结论中正确的是( )
①在空间中,若两条直线不相交,则它们一定平行;②平行于同一条直线的两条直线平行;③一条直线和两条平行直线的一条相交,那么它也和另一条相交;④空间四条直线a,b,c,d,如果a∥b,c∥d,且a∥d,那么b∥c.
A.①②③ B.②④
C.③④ D.②③
B [①错,可以异面.②正确,公理4.③错误,和另一条可以异面.④正确,由平行直线的传递性可知.]
3.已知直线a,b,c,下列三个命题:
①若a∥b,a⊥c,则b⊥c;
②若a∥b,a和c相交,则b和c也相交;
③若a⊥b,a⊥c,则b∥c.
其中,命题正确的是________.(填序号)
① [①项正确;②项不正确,有可能相交也有可能异面;③项不正确,可能平行,可能相交也可能异面.]
4.如图,已知长方体ABCD A′B′C′D′中,AB=2,AD=2,AA′=2.
(1)BC和A′C′所成的角是多少度?
(2)AA′和BC′所成的角是多少度?
[解] (1)因为BC∥B′C′,
所以∠B′C′A′是异面直线A′C′与BC所成的角.
在Rt△A′B′C′中,A′B′=2,
B′C′=2,所以∠B′C′A′=45°.
因此,异面直线BC和A′C′所成的角为45°.
(2)因为AA′∥BB′,
所以∠B′BC′是异面直线AA′和BC′所成的角.
在Rt△BB′C′中,B′C′=AD=2,BB′=AA′=2,
所以BC′=4,∠B′BC′=60°.
因此,异面直线AA′与BC′所成的角为60°.
8 / 10
【第一课时】
【教学目标】
掌握空间图形的基本事实1、2、3.
【教学重难点】
掌握平面的基本事实及推论.
【教学过程】
一、基础铺垫
平面的基本事实及推论:
公理 内容 图形 符号
基本事实1 过不在一条直线上的三点,有且只有一个平面 A,B,C三点不共线 存在唯一的平面α使A,B,C∈α
基本事实2 如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内 A∈l,B∈l,且A∈α,B∈α l α
基本事实3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线 P∈α,P∈β α∩β=l,且P∈l
推论1 一条直线和该直线外一点确定一个平面(图①)。
推论2 两条相交直线确定一个平面(图②)。
推论3 两条平行直线确定一个平面(图③)。
思考1:两个平面的交线可能是一条线段吗?
提示:不可能.由公理3知两平面的交线是一条直线.
思考2:经过空间任意三点能确定一个平面吗?
提示:不一定.只有经过空间不共线的三点才能确定一个平面.
二、合作探究
1.点线共面问题
【例1】 证明:两两相交且不共点的三条直线在同一平面内.
[思路探究] 先说明两条相交直线确定一个平面,然后证明另外一条直线也在该平面内.或利用公理1的推论,说明三条相交直线分别确定两个平面α,β,然后证明α,β重合.
[解] 已知:如图所示,l1∩l2=A,l2∩l3=B,l1∩l3=C.
求证:直线l1,l2,l3在同一平面内.
法一:∵l1∩l2=A,∴l1和l2确定一个平面α.
∵l2∩l3=B,∴B∈l2又l2α,∴B∈α.
同理可证C∈α,又B∈l3,C∈l3,∴l3α.
∴直线l1,l2,l3在同一平面内.
法二:∵l1∩l2=A,∴l1,l2确定一个平面α.
∵l2∩l3=B,∴l2,l3确定一个平面β.
∵A∈l2,l2α,∴A∈α.
∵A∈l2,l2β,∴A∈β.
同理可证,B∈α,B∈β,C∈α,C∈β.
∵不共线的三个点A,B,C既在平面α内,又在平面β内,
∴平面α和平面β重合,即直线l1,l2,l3在同一平面内.
【规律方法】
证明点、线共面问题的理论依据是公理1和公理2,常用方法有:
(1)先由部分点、线确定一个面,再证其余的点、线都在这个平面内,即用“纳入法”;
(2)先由其中一部分点、线确定一个平面α,其余点、线确定另一个平面β,再证平面α与β重合,即用“同一法”;
(3)假设不共面,结合题设推出矛盾,即用“反证法”.
2.点共线与线共点问题
[探究问题]
(1)如图所示,在空间四边形各边AD,AB,BC,CD上分别取E,F,G,H四点,如果EF,GH交于一点P,那么点P,B,D共线吗?请说明理由.
提示:连接BD(图略).
∵EF,HG相交于一点P,
且EF平面ABD,GH平面CBD,
∴P∈平面ABD且P∈平面CBD.
又平面ABD∩平面BCD=BD,
∴P∈BD,∴点P,B,D共线.
(2)如图,在正方体ABCD A1B1C1D1中,设线段A1C与平面ABC1D1交于点Q,能否判断B,Q,D1三点共线?
提示:∵D1∈平面ABC1D1,D1∈平面A1D1CB,B∈平面ABC1D1,B∈平面A1D1CB,
∴平面ABC1D1∩平面A1D1CB=BD1.
∵A1C∩平面ABC1D1=Q,且A1C平面A1D1CB,
∴Q∈平面A1D1CB,Q∈平面ABC1D1,
∴Q在两平面的交线BD1上,∴B,Q,D1三点共线.
【例2】 已知△ABC在平面α外,它的三边所在的直线分别交平面α于P,Q,R(如图).求证:P,Q,R三点共线.
[思路探究] 解答本题可以先选两点确定一条直线,再证明第三点也在这条直线上.
[证明] 法一:∵AB∩α=P,∴P∈AB,P∈平面α.
又AB平面ABC,∴P∈平面ABC.
∴由公理3可知,点P在平面ABC与平面α的交线上.
同理可证Q,R也在平面ABC与平面α的交线上.
∴P,Q,R三点共线.
法二:∵AP∩AR=A,
∴直线AP与直线AR确定平面APR.
又∵AB∩α=P,AC∩α=R,
∴平面APR∩平面α=PR.
∵B∈平面APR,C∈平面APR,
∴BC平面APR.又∵Q∈直线BC,
∴Q∈平面APR.又Q∈α,
∴Q∈PR,∴P,Q,R三点共线.
【规律方法】
1.证明多点共线主要采用如下两种方法:一是首先确定两个平面,然后证明这些点是这两个平面的公共点,再根据公理3,这些点都在这两个平面的交线上;二是选择其中两点确定一条直线,然后再证明其他的点都在这条直线上.
2.证明三线共点问题的方法主要是:先确定两条直线交于一点,再证明该点是这两条直线所在平面的公共点,第三条直线是这两个平面的交线.
三、课堂小结
1.解决立体几何问题首先应过好三大语言关,即实现这三种语言的相互转换,正确理解集合符号所表示的几何图形的实际意义,恰当地用符号语言描述图形语言,将图形语言用文字语言描述出来,再转换为符号语言.文字语言和符号语言在转换的时候,要注意符号语言所代表的含义,作直观图时,要注意线的实虚.
2.在处理点线共面、三点共线及三线共点问题时初步体会三个公理的作用,突出先部分再整体的思想.
四、课堂检测
1.思考辨析
(1)不平行的两条直线的位置关系为相交. ( )
(2)两个平面的交线可以是一条线段. ( )
(3)直线l在平面α内,可以表示为“lα”. ( )
(4)平面内的直线与不在该平面内的直线互为异面直线. ( )
[解析] (1)×,不平行的两条直线的位置关系为相交或异面,故(1)错.
(2)×,两个平面的交线是直线,故(2)错.
(3)√,正确.
(4)×,可能相交或平行,故(4)错.
[答案] (1)× (2)× (3)√ (4)×
2.设平面α与平面β交于直线l,A∈α,B∈α,且直线AB∩l=C,则直线AB∩β=________.
C [∵α∩β=l,AB∩l=C,∴C∈β,C∈AB,∴AB∩β=C.]
3.若a,b是异面直线,b,c是异面直线,则直线a与直线c的位置关系是________.
平行、相交或异面 [两条直线a,c都与同一条直线b是异面直线,则这两条直线平行、相交或异面都有可能.]
4.已知直线a∥b,直线l与a,b都相交,求证:过a,b,l有且只有一个平面.
[解] 如图所示.∵a∥b,
∴直线a,b确定一个平面,设这个平面为α.
设a∩l=A,b∩l=B,∴A∈α,B∈α,且A∈l,B∈l,
∴lα.即过a,b,l有且只有一个平面.
【第二课时】
【教学目标】
1.掌握基本事实4和“等角定理”.
2.理解异面直线所成的角及直线与直线垂直的定义.
3.会求异面直线所成的角.
【教学重难点】
理解异面直线所成的角及直线与直线垂直的定义.
【教学过程】
一、基础铺垫
1.基本事实4
(1)条件:两条直线平行于同一条直线.
(2)结论:这两条直线平行.
(3)符号表述:.
2.等角定理
(1)条件:空间中,如果两个角的两条边分别对应平行.
(2)结论:这两个角相等或互补.
思考1:当一个角的两边与另一个角的两边分别平行时,试问这两个角在什么情况下相等,在什么情况下互补?
提示:当两个角的两边分别平行且方向相同或相反时,这两个角相等;当两个角的一组边的方向相同,而另一组边的方向相反时,这两个角互补.
3.空间两条直线的位置关系
共面直线
异面直线:不共面的两条直线且没有公共点.
4.异面直线所成的角
定义 过空间任意一点P分别引两条异面直线a,b的平行线l1,l2(a∥l1,b∥l2),这两条相交直线所成的锐角(或直角)就是异面直线a,b所成的角
取值 范围 异面直线所成的角θ的取值范围:
特例 当θ=时,a与b互相垂直,记作a⊥b
思考2:分别在两个平面内的两条直线一定是异面直线吗?
提示:不一定.可能是相交,平行或异面.
二、合作探究
1.基本事实4的应用
【例1】 如图,已知E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点.
(1)求证:四边形EFGH是平行四边形;
(2)若四边形EFGH是矩形,求证:AC⊥BD.
[解] (1)如题图,在△ABD中,
∵EH是△ABD的中位线,
∴EH∥BD,EH=BD.
又FG是△CBD的中位线,
∴FG∥BD,FG=BD,
∴FG∥EH,∴E,F,G,H四点共面,又FG=EH,
∴四边形EFGH是平行四边形.
(2)由(1)知EH∥BD,同理AC∥GH.又∵四边形EFGH是矩形,∴EH⊥GH,∴AC⊥BD.
【规律方法】
空间中证明两直线平行的方法:
(1)借助平面几何知识证明,如三角形中位线性质、平行四边形的性质、用成比例线段证平行等.
(2)利用公理4证明,即证明两直线都与第三条直线平行.
2.等角定理的应用
【例2】 如图,在正方体ABCD A1B1C1D1中,M,M1分别是棱AD和A1D1的中点.
(1)求证:四边形BB1M1M为平行四边形;
(2)求证:∠BMC=∠B1M1C1.
[解] (1)∵ABCD A1B1C1D1为正方体,
∴ADA1D1,
又M,M1分别为棱AD,A1D1的中点,
∴AMA1M1,
∴四边形AMM1A1为平行四边形,
∴MM1AA1.
又AA1=BB1且AA1∥BB1,
∴MM1BB1,
∴四边形BB1M1M为平行四边形.
(2)法一:由(1)知四边形BB1M1M为平行四边形,
∴B1M1∥BM.
同理可得四边形CC1M1M为平行四边形,
∴C1M1∥CM.
由平面几何知识可知,∠BMC和∠B1M1C1都是锐角,
∴∠BMC=∠B1M1C1.
法二:由(1)知四边形BB1M1M为平行四边形,
∴B1M1=BM.
同理可得四边形CC1M1M为平行四边形,
∴C1M1=CM.
又∵B1C1=BC,∴△BCM≌△B1C1M1,
∴∠BMC=∠B1M1C1.
【规律方法】
空间等角定理实质上是由以下两个结论组成的:
(1)若一个角的两边与另一个角的两边分别对应平行且方向都相同或相反,那么这两个角相等;
(2)若一个角的两边与另一个角的两边分别平行,有一组对边方向相同,另一组对边方向相反,那么这两个角互补.
3.求异面直线所成的角
[探究问题]
(1)已知直线a,b是两条异面直线,如何作出这两条异面直线所成的角?
提示:如图,在空间中任取一点O,作直线a′∥a,b′∥b,则两条相交直线a′,b′所成的锐角或直角θ即两条异面直线a,b所成的角.
(2)a′与b′所成角的大小与什么有关,与点O的位置有关吗?通常点O取在什么位置?
提示:a′与b′所成角的大小只由a,b的相互位置确定,与点O的选择无关,一般情况下为了简便,点O选取在两条直线中的一条直线上.
【例3】 如图,在空间四边形ABCD中,AD=BC=2,E,F分别是AB,CD的中点,若EF=,求异面直线AD,BC所成角的大小.
[思路探究] 根据求异面直线所成角的方法,将异面直线AD,BC平移到同一平面内解决.
[解] 如图,取BD的中点M,连接EM,FM.
因为E,F分别是AB,CD的中点,
所以EMAD,FMBC,
则∠EMF或其补角就是异面直线AD,BC所成的角.
因为AD=BC=2,所以EM=MF=1,
在等腰△MEF中,过点M,作MH⊥EF于H,
在Rt△MHE中,EM=1,EH=EF=,
则sin∠EMH=,于是∠EMH=60°,
则∠EMF=2∠EMH=120°.
所以异面直线AD,BC所成的角为∠EMF的补角,
即异面直线AD,BC所成的角为60°.
【规律方法】求两条异面直线所成的角的一般步骤:
(1)构造:根据异面直线的定义,用平移法 常用三角形中位线、平行四边形性质等 作出异面直线所成的角.
(2)证明:证明作出的角就是要求的角.
(3)计算:求角度,常放在三角形内求解.
(4)结论:若求出的角是锐角或直角,则它就是所求异面直线所成的角;若求出的角是钝角,则它的补角就是所求异面直线所成的角.
三、课堂总结
1.判定两直线的位置关系的依据就在于两直线平行、相交、异面的定义.很多情况下,定义就是一种常用的判定方法.
2.在研究异面直线所成角的大小时,通常把两条异面直线所成的角转化为两条相交直线所成的角.将空间问题向平面问题转化,这是我们学习立体几何的一条重要的思维途径.需要强调的是,两条异面直线所成角的范围为(0°,90°],解题时经常结合这一点去求异面直线所成角的大小.
四、课堂练习
1.思考辨析
(1)已知a,b,c,d是四条直线,若a∥b,b∥c,c∥d,则a∥d.
( )
(2)两条直线a,b没有公共点,那么a与b是异面直线. ( )
(3)若a,b是两条直线,α,β是两个平面,且aα,bβ,则a,b是异面直线. ( )
[解析] (2)×,也可能平行.
(3)×,可能平行、相交、异面.
[答案] (1)√ (2)× (3)×
2.下列结论中正确的是( )
①在空间中,若两条直线不相交,则它们一定平行;②平行于同一条直线的两条直线平行;③一条直线和两条平行直线的一条相交,那么它也和另一条相交;④空间四条直线a,b,c,d,如果a∥b,c∥d,且a∥d,那么b∥c.
A.①②③ B.②④
C.③④ D.②③
B [①错,可以异面.②正确,公理4.③错误,和另一条可以异面.④正确,由平行直线的传递性可知.]
3.已知直线a,b,c,下列三个命题:
①若a∥b,a⊥c,则b⊥c;
②若a∥b,a和c相交,则b和c也相交;
③若a⊥b,a⊥c,则b∥c.
其中,命题正确的是________.(填序号)
① [①项正确;②项不正确,有可能相交也有可能异面;③项不正确,可能平行,可能相交也可能异面.]
4.如图,已知长方体ABCD A′B′C′D′中,AB=2,AD=2,AA′=2.
(1)BC和A′C′所成的角是多少度?
(2)AA′和BC′所成的角是多少度?
[解] (1)因为BC∥B′C′,
所以∠B′C′A′是异面直线A′C′与BC所成的角.
在Rt△A′B′C′中,A′B′=2,
B′C′=2,所以∠B′C′A′=45°.
因此,异面直线BC和A′C′所成的角为45°.
(2)因为AA′∥BB′,
所以∠B′BC′是异面直线AA′和BC′所成的角.
在Rt△BB′C′中,B′C′=AD=2,BB′=AA′=2,
所以BC′=4,∠B′BC′=60°.
因此,异面直线AA′与BC′所成的角为60°.
8 / 10
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
