6.6.1 柱、锥、台的侧面展开与面积 教案
文档属性
| 名称 | 6.6.1 柱、锥、台的侧面展开与面积 教案 |
|
|
| 格式 | docx | ||
| 文件大小 | 82.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-23 00:00:00 | ||
图片预览


文档简介
柱、锥、台的侧面展开与面积
【教学目标】 【核心素养】
1.理解圆柱、圆锥、圆台的表面积的概念,了解它们的侧面展开图.(重点) 2.掌握直棱柱、正棱锥、正棱台的表面积公式,并会求它们的表面积.(难点) 1.通过学习柱体、锥体、台体表面积的侧面展开图,培养直观想象的核心素养. 2.借助柱体、锥体、台体的表面积计算,培养数学运算的核心素养.
【教学过程】
一、基础铺垫
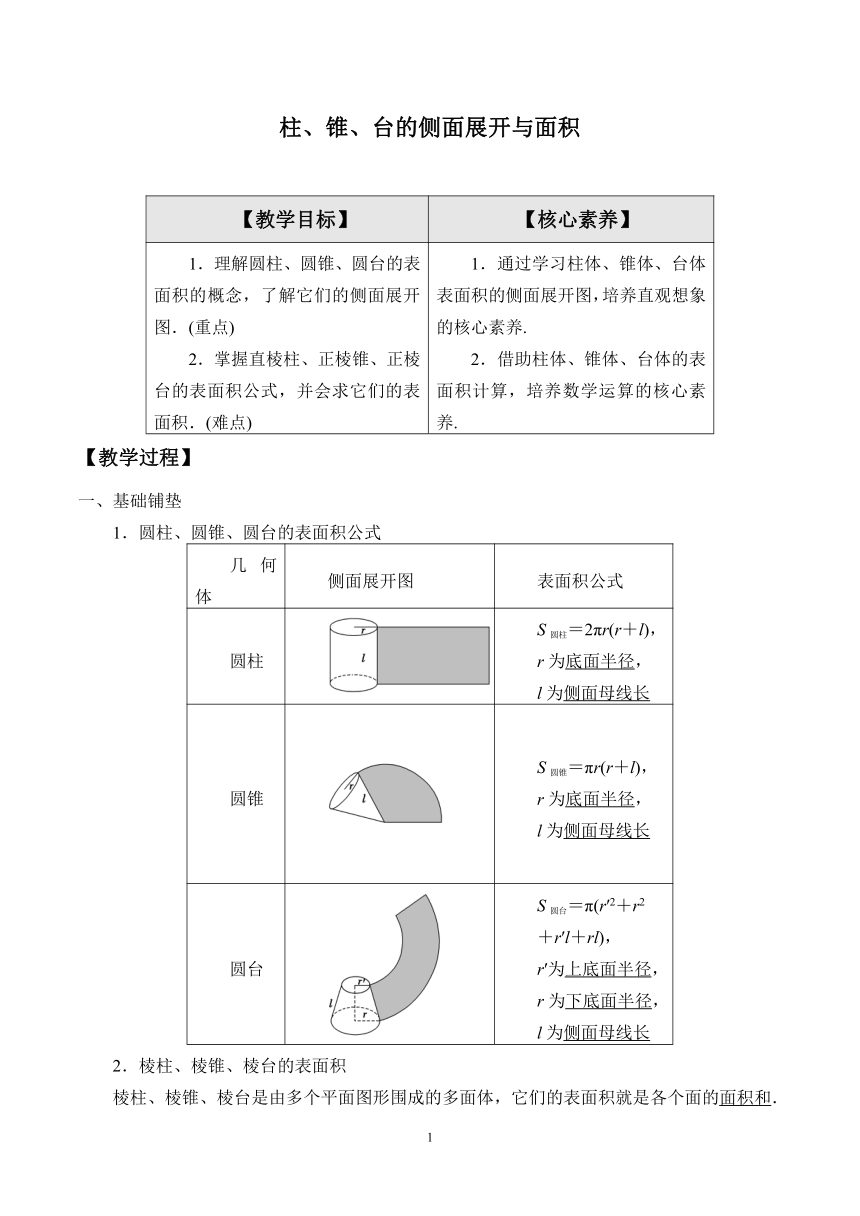
1.圆柱、圆锥、圆台的表面积公式
几何体 侧面展开图 表面积公式
圆柱 S圆柱=2πr(r+l), r为底面半径, l为侧面母线长
圆锥 S圆锥=πr(r+l), r为底面半径, l为侧面母线长
圆台 S圆台=π(r′2+r2 +r′l+rl), r′为上底面半径, r为下底面半径, l为侧面母线长
2.棱柱、棱锥、棱台的表面积
棱柱、棱锥、棱台是由多个平面图形围成的多面体,它们的表面积就是各个面的面积和.
其中,S直棱柱侧=ch,S直棱锥侧=ch’/2,S正棱台侧=(c1+c2)h’/2.
二、合作探究
1.求圆柱、圆锥、圆台的表面积
【例1】 一个直角梯形的两底长为2和5,高为4,将其绕较长的底旋转一周,求所得旋转体的表面积.
[思路探究] →
[解] 如图所示,梯形ABCD中,AD=2,AB=4,BC=5.
作DM⊥BC,垂足为点M,则DM=4,MC=5-2=3,
在Rt△CMD中,由勾股定理得CD==5.
在旋转生成的旋转体中,AB形成一个圆面,AD形成一个圆柱的侧面,CD形成一个圆锥的侧面,设其面积分别为S1,S2,S3,则S1=π×42=16π,S2=2π×4×2=16π,S3=π×4×5=20π,
故此旋转体的表面积为S=S1+S2+S3=52π.
【规律方法】
(1)圆柱、圆锥、圆台的相关几何量都集中体现在轴截面上,因此准确把握轴截面中的相关量是求解旋转体表面积的关键.
(2)棱锥及棱台的表面积计算常借助斜高、侧棱及其在底面的射影与高、底面边长等构成的直角三角形(或梯形)求解.
2.求棱柱、棱锥、棱台的表面积
【例2】 已知正四棱锥底面边长为4,高与斜高夹角为30°.求它的侧面积和表面积.
[思路探究] 根据多面体的侧面积公式,可以先求出相应多面体的底面边长和各侧面的斜高,进而由公式求解.
[解] 如图所示,设正四棱锥的高为PO,斜高为PE,底面边心距为OE,它们组成一个直角三角形POE.
∵OE==2,∠OPE=30°,
∴PE===4.
∴S正四棱锥侧=ch′=×(4×4)×4=32,
S表面积=42+32=48.
即该正四棱锥的侧面积是32,表面积是48.
【规律方法】
(1)要求锥体的侧面积及表面积,要利用已知条件寻求公式中所需的条件,一般用锥体的高、斜高、底面边心距等量组成的直角三角形求解相应的量.
(2)空间几何体的表面积运算,一般是转化为平面几何图形的运算,往往通过解三角形来完成.
三、课堂小结
1.本节课的重点是掌握柱体、锥体、台体、球的表面积的求法,难点是会求组合体的表面积.
2.本节课要重点掌握的规律方法
(1)求空间几何体侧面积、表面积的方法技巧.
(2)求与组合体有关的表面积的方法.
3.本节课的易错点是求与三视图有关的几何体表面积时易把相关数据弄错.
四、课堂练习
1.思考辨析
(1)多面体的表面积等于各个面的面积之和.( )
(2)棱台的侧面展开图是由若干个等腰梯形组成的.( )
(3)沿不同的棱将多面体展开,得到的展开图相同,表面积相等.( )
[解析] (1)正确.多面体的表面积等于侧面积与底面积之和.
(2)错误.棱台的侧面展开图是由若干个梯形组成的,不一定是等腰梯形.
(3)错误.由于剪开的棱不同,同一个几何体的表面展开图可能不是全等形.但是,不论怎么剪,同一个多面体表面展开图的面积是一样的.
[答案] (1)√ (2)× (3)×
2.一个圆柱的侧面展开图是一个正方形,则这个圆柱的表面积与侧面积之比为( )
A. B.
C. D.
A [设圆柱的底面半径为r,高为h,则有h=2πr,所以表面积与侧面积的比为2π(r2+rh)∶2πrh=(r+h)∶h=(2π+1)∶2π.]
3.已知一圆锥的侧面展开图为半圆,且面积为S,求圆锥的底面面积.
[解] 如图,设圆锥底面半径为r,母线长为l,
由题意得
解得r=,
所以底面积为πr2=π×=.
所以圆锥的底面面积为.
1
【教学目标】 【核心素养】
1.理解圆柱、圆锥、圆台的表面积的概念,了解它们的侧面展开图.(重点) 2.掌握直棱柱、正棱锥、正棱台的表面积公式,并会求它们的表面积.(难点) 1.通过学习柱体、锥体、台体表面积的侧面展开图,培养直观想象的核心素养. 2.借助柱体、锥体、台体的表面积计算,培养数学运算的核心素养.
【教学过程】
一、基础铺垫
1.圆柱、圆锥、圆台的表面积公式
几何体 侧面展开图 表面积公式
圆柱 S圆柱=2πr(r+l), r为底面半径, l为侧面母线长
圆锥 S圆锥=πr(r+l), r为底面半径, l为侧面母线长
圆台 S圆台=π(r′2+r2 +r′l+rl), r′为上底面半径, r为下底面半径, l为侧面母线长
2.棱柱、棱锥、棱台的表面积
棱柱、棱锥、棱台是由多个平面图形围成的多面体,它们的表面积就是各个面的面积和.
其中,S直棱柱侧=ch,S直棱锥侧=ch’/2,S正棱台侧=(c1+c2)h’/2.
二、合作探究
1.求圆柱、圆锥、圆台的表面积
【例1】 一个直角梯形的两底长为2和5,高为4,将其绕较长的底旋转一周,求所得旋转体的表面积.
[思路探究] →
[解] 如图所示,梯形ABCD中,AD=2,AB=4,BC=5.
作DM⊥BC,垂足为点M,则DM=4,MC=5-2=3,
在Rt△CMD中,由勾股定理得CD==5.
在旋转生成的旋转体中,AB形成一个圆面,AD形成一个圆柱的侧面,CD形成一个圆锥的侧面,设其面积分别为S1,S2,S3,则S1=π×42=16π,S2=2π×4×2=16π,S3=π×4×5=20π,
故此旋转体的表面积为S=S1+S2+S3=52π.
【规律方法】
(1)圆柱、圆锥、圆台的相关几何量都集中体现在轴截面上,因此准确把握轴截面中的相关量是求解旋转体表面积的关键.
(2)棱锥及棱台的表面积计算常借助斜高、侧棱及其在底面的射影与高、底面边长等构成的直角三角形(或梯形)求解.
2.求棱柱、棱锥、棱台的表面积
【例2】 已知正四棱锥底面边长为4,高与斜高夹角为30°.求它的侧面积和表面积.
[思路探究] 根据多面体的侧面积公式,可以先求出相应多面体的底面边长和各侧面的斜高,进而由公式求解.
[解] 如图所示,设正四棱锥的高为PO,斜高为PE,底面边心距为OE,它们组成一个直角三角形POE.
∵OE==2,∠OPE=30°,
∴PE===4.
∴S正四棱锥侧=ch′=×(4×4)×4=32,
S表面积=42+32=48.
即该正四棱锥的侧面积是32,表面积是48.
【规律方法】
(1)要求锥体的侧面积及表面积,要利用已知条件寻求公式中所需的条件,一般用锥体的高、斜高、底面边心距等量组成的直角三角形求解相应的量.
(2)空间几何体的表面积运算,一般是转化为平面几何图形的运算,往往通过解三角形来完成.
三、课堂小结
1.本节课的重点是掌握柱体、锥体、台体、球的表面积的求法,难点是会求组合体的表面积.
2.本节课要重点掌握的规律方法
(1)求空间几何体侧面积、表面积的方法技巧.
(2)求与组合体有关的表面积的方法.
3.本节课的易错点是求与三视图有关的几何体表面积时易把相关数据弄错.
四、课堂练习
1.思考辨析
(1)多面体的表面积等于各个面的面积之和.( )
(2)棱台的侧面展开图是由若干个等腰梯形组成的.( )
(3)沿不同的棱将多面体展开,得到的展开图相同,表面积相等.( )
[解析] (1)正确.多面体的表面积等于侧面积与底面积之和.
(2)错误.棱台的侧面展开图是由若干个梯形组成的,不一定是等腰梯形.
(3)错误.由于剪开的棱不同,同一个几何体的表面展开图可能不是全等形.但是,不论怎么剪,同一个多面体表面展开图的面积是一样的.
[答案] (1)√ (2)× (3)×
2.一个圆柱的侧面展开图是一个正方形,则这个圆柱的表面积与侧面积之比为( )
A. B.
C. D.
A [设圆柱的底面半径为r,高为h,则有h=2πr,所以表面积与侧面积的比为2π(r2+rh)∶2πrh=(r+h)∶h=(2π+1)∶2π.]
3.已知一圆锥的侧面展开图为半圆,且面积为S,求圆锥的底面面积.
[解] 如图,设圆锥底面半径为r,母线长为l,
由题意得
解得r=,
所以底面积为πr2=π×=.
所以圆锥的底面面积为.
1
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
