9.2.4总体离散程度的估计课件-2021-2022学年高一下学期数学人教A版(2019)必修第二册(共27张PPT)
文档属性
| 名称 | 9.2.4总体离散程度的估计课件-2021-2022学年高一下学期数学人教A版(2019)必修第二册(共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-24 00:00:00 | ||
图片预览








文档简介
(共27张PPT)
第九章 统计
9.2.4 总体离散程度的估计
学习目标
结合实例,能用样本估计总体的离散程度参数(标准差、方差、极差),理解离散程度参数的统计含义
新课程标准
结合实例,能用样本估计总体的离散程度参数(标准差、方差、极差),理解离散程度参数的统计含义
学习 重难点
标准差、方差、极差
总体集中趋势的估计
知识回顾
名称 优点 缺点
众数 ①体现了样本数据的最大集中点; ②容易得到 ①它只能表达样本数据中很少的一部分信息;
②无法客观地反映总体特征
中位数 ①不受少数几个极端数据,即排序靠前或靠后的几个数据的影响; ②容易得到,便于利用中间数据的信息 对极端值不敏感
平均数 能反映出更多关于样本数据全体的信息 任何一个数据的改变都会引起平均数的改变,数据越“离群”,对平均数的影响越大
样本的众数、中位数和平均数常用来表示样本数据的“中心值”,其中众数和中位数容易计算,不受少数几个极端值的影响,但只能表达样本数据中的少量信息. 平均数代表了数据更多的信息,但受样本中每个数据的影响,越极端的数据对平均数的影响也越大.当样本数据质量比较差时,使用众数、中位数或平均数描述数据的中心位置,可能与实际情况产生较大的误差,难以反映样本数据的实际状况,很多时候还不能使我们做出有效决策.
知识回顾
通过上述数据计算得出:甲、乙两名运动员射击成绩的平均数、中位数、众数都是7。从这三个数据来看,两名运动员没有差别。
探索新知
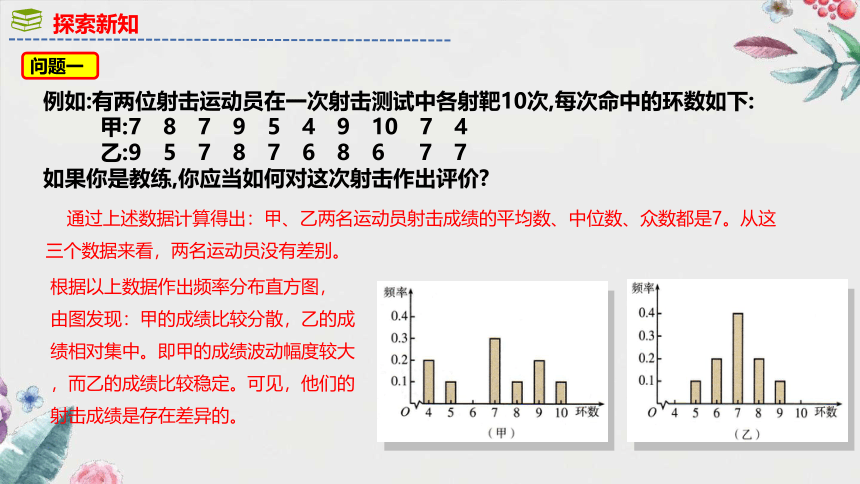
问题一
例如:有两位射击运动员在一次射击测试中各射靶10次,每次命中的环数如下:
甲:7 8 7 9 5 4 9 10 7 4
乙:9 5 7 8 7 6 8 6 7 7
如果你是教练,你应当如何对这次射击作出评价
根据以上数据作出频率分布直方图,
由图发现:甲的成绩比较分散,乙的成绩相对集中。即甲的成绩波动幅度较大,而乙的成绩比较稳定。可见,他们的
射击成绩是存在差异的。
探索新知
问题二
上述问题中,甲、乙的平均数、中位数、众数相同,但二者的射击成绩存在差异,那么,如何度量这种差异呢?
我们可以利用极差进行度量。
根据上述数据计算得:甲的极差=10-4=6 乙的极差=9-5=4
极差在一定程度上刻画了数据的离散程度。
由极差发现甲的成绩波动范围比乙的大。
但由于极差只使用了数据中最大、最小两个值的信息,所含的信息量很少。也就是说,极差度量出的差异误差较大。
方差与标准差
问题三
你还能想出其他刻画数据离散程度的办法吗?
我们知道,如果射击的成绩很稳定,那么大多数的射击成绩离平均成绩不会太远;
相反,如果射击的成绩波动幅度很大,那么大多数的射击成绩离平均成绩会比较远。
因此,我们可以通过这两组射击成绩与它们的平均成绩的“平均距离”来度量成绩的波动幅度。
方差与标准差
如何定义“平均距离”?
思考1
方差与标准差
注意
注意
标准差刻画了数据的离散程度或波动幅度,标准差越大,数据的离散程度越大;标准差越小,数据的离散程度越小.显然,在刻画数据的分散程度上,方差和标准差是一样的.但在解决实际问题中,一般多采用标准差.
在实际问题中,总体平均数和总体标准差都是未知的.就像用样本平均数估计总体平均数一样,通常我们也用样本标准差去估计总体标准差.在随机抽样中,样本标准差依赖于样本的选取,具有随机性.
表示.
标准差:考察样本数据的_ ______________最常用的统计量,是样本数据到_______的一种__________,一般用
标准差的表达式:
分散程度的大小
平均距离
平均数
方差的表达式:
方差与标准差
标准差的范围
是什么?
标准差
s=0表示这组数据中的每个数据到平均数的距离都是0,这组数据的每个数据是相等的。
方差与标准差
问题一
例如:有两位射击运动员在一次射击测试中各射靶10次,每次命中的环数如下:
甲:7 8 7 9 5 4 9 10 7 4
乙:9 5 7 8 7 6 8 6 7 7
如果你是教练,你应当如何对这次射击作出评价
解析:我们可以根据标准差来判断两名运动员的成绩的离散程度,计算可得s甲=2,s乙≈1.095.
即s甲>s乙,由此可知,甲的成绩离散程度大,乙的成绩离散程度小。由此可以估计,乙比甲的成绩稳定。
因此,如果要从这两名选手中选择一名参赛,要看一下他们的平均成绩在所有参赛选手中的位置。
如果两人都排在前面,就选成绩稳定的乙选手,否则选甲。
例一
甲、乙两机床同时加工直径为100 cm的零件,为检验质量,各从中抽取6件测量,数据为
甲:99 100 98 100 100 103
乙:99 100 102 99 100 100
(1)分别计算两组数据的平均数及方差;
(2)根据计算结果判断哪台机床加工零件的质量更稳定.
解析:(1) x 甲=(99+100+98+100+100+103)=100,
x 乙= (99+100+102+99+100+100)=100.
s2甲 = [(99-100)2+(100-100)2+(98-100)2+(100-100)2+(100-100)2+(103-100)2]=,
s2乙 = [(99-100)2+(100-100)2+(102-100)2+(99-100)2+(100-100)2+(100-100)2]=1.
(2)两台机床所加工零件的直径的平均值相同,又s2甲 >s2乙 ,所以乙机床加工零件的质量更稳定.
名师提醒
平均数向我们提供了样本数据的重要信息,一组数据的平均数可以反映出这组数据的一般情况.但当样本数据的平均数相等或相差不多时,就要用样本数据的离散程度来估计总体的离散程度.而样本数据的离散程度,一般由标准差来衡量.
变式练习1
为了选拔参加自行车比赛的选手,对自行车运动员甲,乙两人在相同条件下进行了6次测试,测得他们的最大速度(单位:m/s)的数据如下:
甲 27 38 30 37 35 31
乙 33 29 38 34 28 36
(1)分别求出甲、乙运动员的中位数;
(2)估计甲、乙两运动员的最大速度的平均数和方差,并判断谁参加比赛更合适.
变式练习1
为了选拔参加自行车比赛的选手,对自行车运动员甲,乙两人在相同条件下进行了6次测试,测得他们的最大速度(单位:m/s)的数据如下:
甲 27 38 30 37 35 31
乙 33 29 38 34 28 36
(1)分别求出甲、乙运动员的中位数;
(2)估计甲、乙两运动员的最大速度的平均数和方差,并判断谁参加比赛更合适.
(1)甲的中位数为:(35+31)/2 =33,乙的中位数为:(33+34)/2 =33.5.
(2)甲的平均数为:x甲=1/6 (27+30+31+35+37+38)=33,
乙的平均数为:x乙=1/6 (28+29+33+34+36+38)=33,
甲的方差为:S2甲= (36+9+4+4+16+25)= ,
乙的方差为:S2乙= (25+16+1+9+25)= ,
甲、乙的平均数相等,乙的方差更小,则乙的发挥更稳定,故乙参加比赛更合适.
例二(教材212页例6)
在对树人中学高一年级学生身高的调查中,采用样本量比例分配的分层随机抽样,如果不知道样本数据,只知道抽取了男生23人,其平均数和方差分别为170.6和12.59,抽取了女生27人,其平均数和方差分别为160.6和38.62.你能由这些数据计算出总样本的方差,并对高一年级全体学生的身
高方差作出估计吗
解:把男生样本记为x1,x 2,…,x23,其平均数记为元,方差记为;把女生样本记为y1,y2,…,y23,其平均数记为,方差记为;把总样本数据的平均数记为,方差记为s2.
根据方差的定义,总样本方差为
==
由=-23=0,得=2=0
同理可得=0
因此=
=
由=170.6,=160.6,根据按比例分配分层随机抽样总样本平均数与各层样本平均数的关系,可得总样本平均数为
==
把已知的男生、女生样本平均数和方差的取值代入①,可得
=51.4862
我们可以计算出总样本的方差为51.4862,并据此估计高一年级学生身高的总体方差为51.486 2.
样本标准差刻画了数据离平均数波动的幅度大小,平均数和标准差一起能反映数据取值的信息.例如,根据9.2.1节中100户居民用户的月均用水量数据,可以计算出样本平均数∶=8.79,样本标准差s6.20.
-s2.59,+s=14.99,-2s=-3.61,+2s =21.19.
如图9.2-14所示,可以发现,这100个数据中大部分
落在区间[-s,+s]=[2.59,14.99]内,
在区间[-2s+2s]=[-3.61,21.19]外的只有7个.
也就是说,绝大部分数据落在[-2s,+2s]内.
例二(教材212页例6)
变式练习2
某学校有高中学生500 人,其中男生320 人,女生180人.有人为了获得该校全体高中学生的身高信息,采用分层抽样的方法抽取样本,并观测样本的指标值(单位:cm),计算得男生样本的均值为173.5,方差为17,女生样本的均值为163.83,方差为30.03.
(1)根据以上信息,能够计算出总样本的均值和方差吗 为什么
(2)如果已知男、女样本量按比例分配,你能计算出总样本的均值和方差各为多少吗
(3)如果已知男、女的样本量都是25,你能计算出总样本的均值和方差各为多少吗 它们分别作为
总体均值和方差的估计合适吗 为什么
【解析】(1)不能,因为没有给出男、女生的样本量,或者男、女生样本量的比例,
故无法计算出总样本的均值和方差;
(2)总样本的均值为:
总样本的方差为:+
变式练习2
某学校有高中学生500 人,其中男生320 人,女生180人.有人为了获得该校全体高中学生的身高信息,采用分层抽样的方法抽取样本,并观测样本的指标值(单位:cm),计算得男生样本的均值为173.5,方差为17,女生样本的均值为163.83,方差为30.03.
(1)根据以上信息,能够计算出总样本的均值和方差吗 为什么
(2)如果已知男、女样本量按比例分配,你能计算出总样本的均值和方差各为多少吗
(3)如果已知男、女的样本量都是25,你能计算出总样本的均值和方差各为多少吗 它们分别作为
总体均值和方差的估计合适吗 为什么
(3)总样本的均值为:
总样本的方差为:+
它们分别作为总体均值和方差不合适,因为抽样中未按比例进行分层抽样,所以总体中每个个体被抽到的可能性不完全相同因而样本的代表性差,所以作为总体的估计不合适.
例三
从某企业生成的产品生产线上随机抽取200件产品,测量这批产品的一项质量指标值,由测量结果得如图所示的频率分布直方图:
(1)估计这批产品质量指标值的样本平均和样本方差s2(同一组中的数据用该组区间的中点值做代表);
(2)若该种产品的等级及相应等级产品的利润(每件)参照以下规则(其中Z为产品质量指标值):当Z∈(-s,+s)该产品定为一等品,企业可获利200元;当Z∈(-2s,+2s)且Z (-s,+s)该产品定为二等品,企业可获利100元;当Z∈(-3s,+3s)且Z (-2s,+2s),该产品定为三等品,企业将损失500元;否则该产品定为不合格品,企业将损失1000元.若测得一箱产品(5件)的质量指标数据分别为:76,85,93,105,112,求该箱产品的利润;(参考数据:26 =5.10)
解析:(1)质量指标的样本平均数:
=80×0.06+90×0.26+100×0.38+110×0.22+120×0.08=100,
质量指标的样本方差为:
s2=(-20)2×0.06+(-10)2×0.26+102×0.22+202×0.08=104,
∴估计这批产品质量指标值的样本平均=100,样本方差s2=104.
例三
从某企业生成的产品生产线上随机抽取200件产品,测量这批产品的一项质量指标值,由测量结果得如图所示的频率分布直方图:
(2)若该种产品的等级及相应等级产品的利润(每件)参照以下规则(其中Z为产品质量指标值):当Z∈(-s,+s该产品定为一等品,企业可获利200元;当Z∈(-2s,+2s)且Z (-s,+s)该产品定为二等品,企业可获利100元;当Z∈(-3s,+3s)且Z (-2s,+2s),该产品定为三等品,企业将损失500元;否则该产品定为不合格品,企业将损失1000元.若测得一箱产品(5件)的质量指标数据分别为:76,85,93,105,112,求该箱产品的利润;(参考数据:=5.10)
(2)由(1)知=100,s=104 ≈10.2
∵(-s,+s)=(89.8,110.2),(-2s,+2s)=(79.6,120.4),(-3s,+3s)=(69.4,130.6),
由题意得5件产品中有一等品2件:93,105,有二等品2件:85,112,有三等品1件:76,
∴根据规则该箱产品的利润为:2×200+2×100+1×(-500)=100元.
课堂检测
1.不经过计算,你能给下列各组数的方差排序吗
(1)5,5,5,5,5,5,5,5,5;
(2)4,4,4,5,5,5,6,6,6;
(3) 3,3,4,4,5,6,6,7,7;
(4) 2,2,2,2,5,8,8,8,8.
2.数据x1,x2,…,xn的方差为s2,数据y1,y2,…,yn的方差为s2y,a,b为常数.证明:
(1)如果y1=x1+b,y2=x2+b,…,yn=xn+b,那么s2y=s2x;
(2)如果=,=,…,=,那么s2y=a2s2x.
(2)如果=+b,=+b,…,=+b,那么s2y=a2s2x.
课堂检测
2.数据x1,x2,…,xn的方差为s2,数据y1,y2,…,yn的方差为s2y,a,b为常数.证明:
(1)如果y1=x1+b,y2=x2+b,…,yn=xn+b,那么s2y=s2x;
(2)如果=+b,=+b,…,=+b,那么s2y=a2s2x.
(2)如果=+b,=+b,…,=+b,那么s2y=a2s2x.
课堂检测
2.数据x1,x2,…,xn的方差为s2,数据y1,y2,…,yn的方差为s2y,a,b为常数.证明:
(1)如果y1=x1+b,y2=x2+b,…,yn=xn+b,那么s2y=s2x;
(2)如果=+b,=+b,…,=+b,那么s2y=a2s2x.
(2)如果=+b,=+b,…,=+b,那么s2y=a2s2x.
课堂检测
平均数、方差性质
课堂检测
课堂检测
1.极差的定义及特征:
2.方差、标准差的定义及特征
总体方差、总体标准差的定义
样本方差、样本标准差的定义
3.会求方差、标准差,并做出决策
4.方差的运算性质:
5.会求分层抽样的方差
课堂小结
第九章 统计
9.2.4 总体离散程度的估计
学习目标
结合实例,能用样本估计总体的离散程度参数(标准差、方差、极差),理解离散程度参数的统计含义
新课程标准
结合实例,能用样本估计总体的离散程度参数(标准差、方差、极差),理解离散程度参数的统计含义
学习 重难点
标准差、方差、极差
总体集中趋势的估计
知识回顾
名称 优点 缺点
众数 ①体现了样本数据的最大集中点; ②容易得到 ①它只能表达样本数据中很少的一部分信息;
②无法客观地反映总体特征
中位数 ①不受少数几个极端数据,即排序靠前或靠后的几个数据的影响; ②容易得到,便于利用中间数据的信息 对极端值不敏感
平均数 能反映出更多关于样本数据全体的信息 任何一个数据的改变都会引起平均数的改变,数据越“离群”,对平均数的影响越大
样本的众数、中位数和平均数常用来表示样本数据的“中心值”,其中众数和中位数容易计算,不受少数几个极端值的影响,但只能表达样本数据中的少量信息. 平均数代表了数据更多的信息,但受样本中每个数据的影响,越极端的数据对平均数的影响也越大.当样本数据质量比较差时,使用众数、中位数或平均数描述数据的中心位置,可能与实际情况产生较大的误差,难以反映样本数据的实际状况,很多时候还不能使我们做出有效决策.
知识回顾
通过上述数据计算得出:甲、乙两名运动员射击成绩的平均数、中位数、众数都是7。从这三个数据来看,两名运动员没有差别。
探索新知
问题一
例如:有两位射击运动员在一次射击测试中各射靶10次,每次命中的环数如下:
甲:7 8 7 9 5 4 9 10 7 4
乙:9 5 7 8 7 6 8 6 7 7
如果你是教练,你应当如何对这次射击作出评价
根据以上数据作出频率分布直方图,
由图发现:甲的成绩比较分散,乙的成绩相对集中。即甲的成绩波动幅度较大,而乙的成绩比较稳定。可见,他们的
射击成绩是存在差异的。
探索新知
问题二
上述问题中,甲、乙的平均数、中位数、众数相同,但二者的射击成绩存在差异,那么,如何度量这种差异呢?
我们可以利用极差进行度量。
根据上述数据计算得:甲的极差=10-4=6 乙的极差=9-5=4
极差在一定程度上刻画了数据的离散程度。
由极差发现甲的成绩波动范围比乙的大。
但由于极差只使用了数据中最大、最小两个值的信息,所含的信息量很少。也就是说,极差度量出的差异误差较大。
方差与标准差
问题三
你还能想出其他刻画数据离散程度的办法吗?
我们知道,如果射击的成绩很稳定,那么大多数的射击成绩离平均成绩不会太远;
相反,如果射击的成绩波动幅度很大,那么大多数的射击成绩离平均成绩会比较远。
因此,我们可以通过这两组射击成绩与它们的平均成绩的“平均距离”来度量成绩的波动幅度。
方差与标准差
如何定义“平均距离”?
思考1
方差与标准差
注意
注意
标准差刻画了数据的离散程度或波动幅度,标准差越大,数据的离散程度越大;标准差越小,数据的离散程度越小.显然,在刻画数据的分散程度上,方差和标准差是一样的.但在解决实际问题中,一般多采用标准差.
在实际问题中,总体平均数和总体标准差都是未知的.就像用样本平均数估计总体平均数一样,通常我们也用样本标准差去估计总体标准差.在随机抽样中,样本标准差依赖于样本的选取,具有随机性.
表示.
标准差:考察样本数据的_ ______________最常用的统计量,是样本数据到_______的一种__________,一般用
标准差的表达式:
分散程度的大小
平均距离
平均数
方差的表达式:
方差与标准差
标准差的范围
是什么?
标准差
s=0表示这组数据中的每个数据到平均数的距离都是0,这组数据的每个数据是相等的。
方差与标准差
问题一
例如:有两位射击运动员在一次射击测试中各射靶10次,每次命中的环数如下:
甲:7 8 7 9 5 4 9 10 7 4
乙:9 5 7 8 7 6 8 6 7 7
如果你是教练,你应当如何对这次射击作出评价
解析:我们可以根据标准差来判断两名运动员的成绩的离散程度,计算可得s甲=2,s乙≈1.095.
即s甲>s乙,由此可知,甲的成绩离散程度大,乙的成绩离散程度小。由此可以估计,乙比甲的成绩稳定。
因此,如果要从这两名选手中选择一名参赛,要看一下他们的平均成绩在所有参赛选手中的位置。
如果两人都排在前面,就选成绩稳定的乙选手,否则选甲。
例一
甲、乙两机床同时加工直径为100 cm的零件,为检验质量,各从中抽取6件测量,数据为
甲:99 100 98 100 100 103
乙:99 100 102 99 100 100
(1)分别计算两组数据的平均数及方差;
(2)根据计算结果判断哪台机床加工零件的质量更稳定.
解析:(1) x 甲=(99+100+98+100+100+103)=100,
x 乙= (99+100+102+99+100+100)=100.
s2甲 = [(99-100)2+(100-100)2+(98-100)2+(100-100)2+(100-100)2+(103-100)2]=,
s2乙 = [(99-100)2+(100-100)2+(102-100)2+(99-100)2+(100-100)2+(100-100)2]=1.
(2)两台机床所加工零件的直径的平均值相同,又s2甲 >s2乙 ,所以乙机床加工零件的质量更稳定.
名师提醒
平均数向我们提供了样本数据的重要信息,一组数据的平均数可以反映出这组数据的一般情况.但当样本数据的平均数相等或相差不多时,就要用样本数据的离散程度来估计总体的离散程度.而样本数据的离散程度,一般由标准差来衡量.
变式练习1
为了选拔参加自行车比赛的选手,对自行车运动员甲,乙两人在相同条件下进行了6次测试,测得他们的最大速度(单位:m/s)的数据如下:
甲 27 38 30 37 35 31
乙 33 29 38 34 28 36
(1)分别求出甲、乙运动员的中位数;
(2)估计甲、乙两运动员的最大速度的平均数和方差,并判断谁参加比赛更合适.
变式练习1
为了选拔参加自行车比赛的选手,对自行车运动员甲,乙两人在相同条件下进行了6次测试,测得他们的最大速度(单位:m/s)的数据如下:
甲 27 38 30 37 35 31
乙 33 29 38 34 28 36
(1)分别求出甲、乙运动员的中位数;
(2)估计甲、乙两运动员的最大速度的平均数和方差,并判断谁参加比赛更合适.
(1)甲的中位数为:(35+31)/2 =33,乙的中位数为:(33+34)/2 =33.5.
(2)甲的平均数为:x甲=1/6 (27+30+31+35+37+38)=33,
乙的平均数为:x乙=1/6 (28+29+33+34+36+38)=33,
甲的方差为:S2甲= (36+9+4+4+16+25)= ,
乙的方差为:S2乙= (25+16+1+9+25)= ,
甲、乙的平均数相等,乙的方差更小,则乙的发挥更稳定,故乙参加比赛更合适.
例二(教材212页例6)
在对树人中学高一年级学生身高的调查中,采用样本量比例分配的分层随机抽样,如果不知道样本数据,只知道抽取了男生23人,其平均数和方差分别为170.6和12.59,抽取了女生27人,其平均数和方差分别为160.6和38.62.你能由这些数据计算出总样本的方差,并对高一年级全体学生的身
高方差作出估计吗
解:把男生样本记为x1,x 2,…,x23,其平均数记为元,方差记为;把女生样本记为y1,y2,…,y23,其平均数记为,方差记为;把总样本数据的平均数记为,方差记为s2.
根据方差的定义,总样本方差为
==
由=-23=0,得=2=0
同理可得=0
因此=
=
由=170.6,=160.6,根据按比例分配分层随机抽样总样本平均数与各层样本平均数的关系,可得总样本平均数为
==
把已知的男生、女生样本平均数和方差的取值代入①,可得
=51.4862
我们可以计算出总样本的方差为51.4862,并据此估计高一年级学生身高的总体方差为51.486 2.
样本标准差刻画了数据离平均数波动的幅度大小,平均数和标准差一起能反映数据取值的信息.例如,根据9.2.1节中100户居民用户的月均用水量数据,可以计算出样本平均数∶=8.79,样本标准差s6.20.
-s2.59,+s=14.99,-2s=-3.61,+2s =21.19.
如图9.2-14所示,可以发现,这100个数据中大部分
落在区间[-s,+s]=[2.59,14.99]内,
在区间[-2s+2s]=[-3.61,21.19]外的只有7个.
也就是说,绝大部分数据落在[-2s,+2s]内.
例二(教材212页例6)
变式练习2
某学校有高中学生500 人,其中男生320 人,女生180人.有人为了获得该校全体高中学生的身高信息,采用分层抽样的方法抽取样本,并观测样本的指标值(单位:cm),计算得男生样本的均值为173.5,方差为17,女生样本的均值为163.83,方差为30.03.
(1)根据以上信息,能够计算出总样本的均值和方差吗 为什么
(2)如果已知男、女样本量按比例分配,你能计算出总样本的均值和方差各为多少吗
(3)如果已知男、女的样本量都是25,你能计算出总样本的均值和方差各为多少吗 它们分别作为
总体均值和方差的估计合适吗 为什么
【解析】(1)不能,因为没有给出男、女生的样本量,或者男、女生样本量的比例,
故无法计算出总样本的均值和方差;
(2)总样本的均值为:
总样本的方差为:+
变式练习2
某学校有高中学生500 人,其中男生320 人,女生180人.有人为了获得该校全体高中学生的身高信息,采用分层抽样的方法抽取样本,并观测样本的指标值(单位:cm),计算得男生样本的均值为173.5,方差为17,女生样本的均值为163.83,方差为30.03.
(1)根据以上信息,能够计算出总样本的均值和方差吗 为什么
(2)如果已知男、女样本量按比例分配,你能计算出总样本的均值和方差各为多少吗
(3)如果已知男、女的样本量都是25,你能计算出总样本的均值和方差各为多少吗 它们分别作为
总体均值和方差的估计合适吗 为什么
(3)总样本的均值为:
总样本的方差为:+
它们分别作为总体均值和方差不合适,因为抽样中未按比例进行分层抽样,所以总体中每个个体被抽到的可能性不完全相同因而样本的代表性差,所以作为总体的估计不合适.
例三
从某企业生成的产品生产线上随机抽取200件产品,测量这批产品的一项质量指标值,由测量结果得如图所示的频率分布直方图:
(1)估计这批产品质量指标值的样本平均和样本方差s2(同一组中的数据用该组区间的中点值做代表);
(2)若该种产品的等级及相应等级产品的利润(每件)参照以下规则(其中Z为产品质量指标值):当Z∈(-s,+s)该产品定为一等品,企业可获利200元;当Z∈(-2s,+2s)且Z (-s,+s)该产品定为二等品,企业可获利100元;当Z∈(-3s,+3s)且Z (-2s,+2s),该产品定为三等品,企业将损失500元;否则该产品定为不合格品,企业将损失1000元.若测得一箱产品(5件)的质量指标数据分别为:76,85,93,105,112,求该箱产品的利润;(参考数据:26 =5.10)
解析:(1)质量指标的样本平均数:
=80×0.06+90×0.26+100×0.38+110×0.22+120×0.08=100,
质量指标的样本方差为:
s2=(-20)2×0.06+(-10)2×0.26+102×0.22+202×0.08=104,
∴估计这批产品质量指标值的样本平均=100,样本方差s2=104.
例三
从某企业生成的产品生产线上随机抽取200件产品,测量这批产品的一项质量指标值,由测量结果得如图所示的频率分布直方图:
(2)若该种产品的等级及相应等级产品的利润(每件)参照以下规则(其中Z为产品质量指标值):当Z∈(-s,+s该产品定为一等品,企业可获利200元;当Z∈(-2s,+2s)且Z (-s,+s)该产品定为二等品,企业可获利100元;当Z∈(-3s,+3s)且Z (-2s,+2s),该产品定为三等品,企业将损失500元;否则该产品定为不合格品,企业将损失1000元.若测得一箱产品(5件)的质量指标数据分别为:76,85,93,105,112,求该箱产品的利润;(参考数据:=5.10)
(2)由(1)知=100,s=104 ≈10.2
∵(-s,+s)=(89.8,110.2),(-2s,+2s)=(79.6,120.4),(-3s,+3s)=(69.4,130.6),
由题意得5件产品中有一等品2件:93,105,有二等品2件:85,112,有三等品1件:76,
∴根据规则该箱产品的利润为:2×200+2×100+1×(-500)=100元.
课堂检测
1.不经过计算,你能给下列各组数的方差排序吗
(1)5,5,5,5,5,5,5,5,5;
(2)4,4,4,5,5,5,6,6,6;
(3) 3,3,4,4,5,6,6,7,7;
(4) 2,2,2,2,5,8,8,8,8.
2.数据x1,x2,…,xn的方差为s2,数据y1,y2,…,yn的方差为s2y,a,b为常数.证明:
(1)如果y1=x1+b,y2=x2+b,…,yn=xn+b,那么s2y=s2x;
(2)如果=,=,…,=,那么s2y=a2s2x.
(2)如果=+b,=+b,…,=+b,那么s2y=a2s2x.
课堂检测
2.数据x1,x2,…,xn的方差为s2,数据y1,y2,…,yn的方差为s2y,a,b为常数.证明:
(1)如果y1=x1+b,y2=x2+b,…,yn=xn+b,那么s2y=s2x;
(2)如果=+b,=+b,…,=+b,那么s2y=a2s2x.
(2)如果=+b,=+b,…,=+b,那么s2y=a2s2x.
课堂检测
2.数据x1,x2,…,xn的方差为s2,数据y1,y2,…,yn的方差为s2y,a,b为常数.证明:
(1)如果y1=x1+b,y2=x2+b,…,yn=xn+b,那么s2y=s2x;
(2)如果=+b,=+b,…,=+b,那么s2y=a2s2x.
(2)如果=+b,=+b,…,=+b,那么s2y=a2s2x.
课堂检测
平均数、方差性质
课堂检测
课堂检测
1.极差的定义及特征:
2.方差、标准差的定义及特征
总体方差、总体标准差的定义
样本方差、样本标准差的定义
3.会求方差、标准差,并做出决策
4.方差的运算性质:
5.会求分层抽样的方差
课堂小结
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
