北师大版数学七年级下册 第六章概率初步过关训练 习题课件(共28张PPT)
文档属性
| 名称 | 北师大版数学七年级下册 第六章概率初步过关训练 习题课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 506.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-24 17:01:00 | ||
图片预览








文档简介
(共28张PPT)
第六章概率初步过关训练
一、选择题(本大题12小题,每小题3分,共36分)
1.在一副扑克牌(54 张,其中王牌两张)中,任意抽一张是王牌的概率是( )
C
2.七(1)班在参加学校 4×100 m 接力赛时,安排了甲、乙、丙、丁四位选手,他们的顺序由抽签随机决定,则甲跑第一棒的概率为( )
D
3.一个布袋里装有3 个红球和 5 个黄球,它们除颜色外其余都相同.从中任意摸出一个球是红球的概率是( )
4.书架上摆放5 本书,其中有 2 本教科书,3 本文学书,从书架上任意抽取 1 本,抽到教科书的概率是 ( )
C
C
5.一个小球在如图S6-1所示的地板上随意滚动,当小球停下时,最终停在地板上阴影部分的概率是( )
A
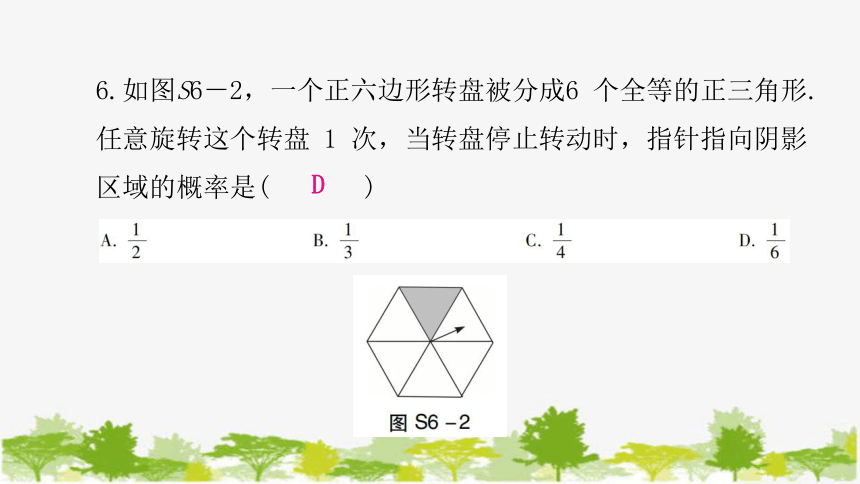
6.如图S6-2,一个正六边形转盘被分成6 个全等的正三角形.任意旋转这个转盘 1 次,当转盘停止转动时,指针指向阴影区域的概率是( )
D
7. 在一个不透明的盒子中装有红、白两种除颜色外完全相同的球,其中有a个白球和3个红球,若每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子.通过大量重复试验后,发现摸到红球的频率稳定在20%左右,则a的值约为( )
A. 9 B. 12 C. 15 D. 18
B
8.一枚质地均匀的正方体骰子,其六个面上分别刻有1,2,3,
4,5,6 的点数,掷这个骰子一次,则掷得面朝上的点数为奇数的概率是 ( )
C
9.小真煮好了25 颗汤圆,其中 15 颗为芝麻汤圆,10 颗为花生汤圆,已知小真想从煮好的汤圆中捞一颗,若每颗汤圆被小真捞到的机会相等,则他捞到花生汤圆的概率为 ( )
C
10.用频率估计概率,可以发现,抛掷一枚硬币,“正面朝上”的概率为0.5,是指( )
A. 连续掷 2 次,结果一定是“正面朝上”和“反面朝上”各 1 次
B. 连续抛掷 100 次,结果一定是“正面朝上”和“反面朝上”各 50 次
C. 抛掷 2n 次硬币,恰好有 n 次“正面朝上”
D. 抛掷 n 次,当 n 越来越大时,“正面朝上”的频率会越来越稳定于 0.5
D
摸球的次数n 100 200 300 500 800 1 000 1 500
摸到白球的次数m 70 128 171 302 481 599 903
0.70 0.64 0.57 0.604 0.601 0.599 0.602
11.在一个不透明的盒子里装着除颜色外完全相同的黑、白两种小球共40个.小颖做摸球试验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色后放回,不断重复上述过程,多次试验后,得到下表中的数据,并得出了四个结论,其中正确的是( )
B
A. 试验1 500 次摸到白球的频率比试验800次的更接近0.6
B. 从该盒子中任意摸出一个小球,摸到白球的频率约为0.6
C. 当试验次数n为2 000时,摸到白球的次数m一定等于1 200
D. 这个盒子中的白球一定有24个
12.某小组做“用频率估计概率”的试验时,统计了某一结果出现的频率,绘制了如图S6-3所示的折线统计图,则符合这一结果的试验最有可能的是( )
在“石头、剪刀、布”的游戏中,
小明随机出的是“剪刀”
B. 一副去掉大、小王的普通扑克牌洗
匀后,从中任抽一张牌的花色是红桃
C. 暗箱中有 1 个红球和 2 个黄球,
它们只有颜色上的区别,从中任取一球是黄球
D. 掷一个质地均匀的正六面体骰子,向上的面的点数是 4
D
二、填空题(本大题6小题,每小题4分,共24分)
13.一个袋中装有6 个红球,5 个黄球,3 个白球,每个球除颜色外都相同,任意摸出一球,摸到 球的可能性最大.
14.在一个箱子里放有1 个白球和 2 个红球,它们除颜色外其余都相同,从箱子里摸出 1 个球,则摸到红球的概率是 .
红
15.向如图S6-4所示的正三角形区域扔沙包(区域中每一个小正三角形除颜色外完全相同),假设沙包击中每一个小三角形是等可能的,扔沙包1 次击中阴影区域的概率等于 .
16. 把标有号码1,2,3,…,10的10个乒乓球放在一个箱子中,摇匀后,从中任意取一个,号码为小于7的奇数的概率是 .
17.一个不透明的袋子中装有除颜色外均相同的8 个黑球、 4 个白球和若干个红球.每次摇匀随机摸出一个球,记下颜色后再放回袋子中,通过大量重复摸球试验后,发现摸到红球的频率稳定于 0.4,由此可估计袋子中约有红球 个.
8
18.农业部门引进一批新麦种,在播种前做了五次发芽试验,目的是想了解一粒这样的麦种发芽情况,实验统计数据如下:
实验的麦种数/粒 500 500 500 500 500
发芽的麦种数/粒 492 487 491 493 489
发芽率/% 98.40 97.40 98.20 98.60 97.80
估计在与实验条件相同的情况下,种一粒这样的麦种发芽的概率约为 .(结果精确到0.01)
0.98
三、解答题(一)(本大题2小题,每小题8分,共16分)
19. 转动如图S6-5所示的转盘(转盘被等分成六份),转盘停止后,指针对着某一数字.
(1)“指针对着2”和“指针对着 1”哪个可能性大?
(2)“指针对着3”和“指针对着 1”哪个可能性大?
解:(1) “指针对着 2”和“指针对着 1”
的可能性相同.
(2) “指针对着1”的可能性大.
20.一个不透明的袋子中有 1 个红球,2 个绿球和 n 个白球,这些球除颜色外都相同.
(1)当n=1 时,从袋中随机摸出 1 个球,摸到红球和摸到白球的可能性 ;(填“相同”或“不相同”)
(2)从袋中随机摸出1 个球,记录其颜色,然后放回.大量重复该试验,发现摸到绿球的频率稳定于 0.2,求 n 的值.
解:(2) 由题意,得2÷0.2=10(个).
10-1-2=7(个).
所以n=7.
相同
四、解答题(二)(本大题2小题,每小题10分,共20分)
21.甲认为如图S6-6所示的A,B两转盘都只有两种颜色,分别转动指针,待指针停止后,指针不是停在红色上就是停在蓝色上,机会一样,都是 50%,你认为对吗?为什么?
解:不对.
因为A转盘上指针停在红色上的概率是 ,停在蓝色上的概率是
所以指针停在红色上和停在蓝色上的机会不一样.
因为B转盘上指针停在红色上的概率是 ,停在蓝色上的概率是 ,
所以指针停在红色上和停在蓝色上的机会一样.
22.某市民政部门今年五一期间举行了“即开式社会福利彩票”销售活动,设置彩票2 000万张(每张彩票 2 元).在这些彩票中,设置了如下的奖项.
奖金/万元 50 15 8 2 …
数量/个 10 20 20 180 …
(1)如果花2元购买1张彩票,那么能得到50万元大奖的概率是多少?
(2)如果花2元购买1张彩票,那么能得到8万元以上(包括8万元)大奖的概率是多少?
解:(1) 因为彩票2 000万张,50万元的彩票有10张,
所以能得到50万元大奖的概率是
(2)因为彩票 2 000 万张,8万元以上(包括 8 万元)的彩票有 10+20+20=50(张),
所以能得到8万以上(包括8万元)大奖的概率是
五、解答题(三)(本大题2小题,每小题12分,共24分)
23.如图S6-7,小林和小芳两人玩游戏,掷骰子定输赢.
(1)朝上一面点数是3 的倍数的情况有哪些?出现朝上一面点数是 3 的倍数的概率是多少?
(2)朝上一面点数不是3 的倍数的情况有哪些?出现朝上一面点数不是 3 的倍数的概率是多少?
(3)请你评判一下,这样的规则公平吗?
解:(1) 朝上一面点数是 3 的倍数的情况有 3,6 两种,
出现朝上一面点数是3 的倍数的概率为
(2) 朝上一面点数不是3 的倍数的情况有 1,2,4,5 四种,
出现朝上一面点数不是3 的倍数的概率为
(3) 出现朝上一面点数是3 的倍数的概率小于出现朝上一面点数不是 3 的倍数的概率,规则不公平.
24. 某批足球的质量检测结果如下:
抽取足球数n 100 200 400 600 800 1 000
合格的频数m 93 192 384 564 759 950
合格的频率 0.93 0.96 0.96 0.94
(1)填写表中的空格.(结果精确到0.01)
(2)请在图S6-8中画出合格的频率的折线统计图.
(3)从这批足球任意抽取的一只足球是合格品的概率估计值是多少?并说明理由.
0.95
0.95
解:(2) 如答图S6-1.
(3) 从这批足球任意抽取的一只足球是合格品的概率估计值是0.95.
因为从折线统计图中可知,随着试验次数的增大,频率逐渐稳定到常数0.95 附近,
所以从这批足球任意抽取的一只足球是合格品的概率估计值是0.95.
谢 谢
第六章概率初步过关训练
一、选择题(本大题12小题,每小题3分,共36分)
1.在一副扑克牌(54 张,其中王牌两张)中,任意抽一张是王牌的概率是( )
C
2.七(1)班在参加学校 4×100 m 接力赛时,安排了甲、乙、丙、丁四位选手,他们的顺序由抽签随机决定,则甲跑第一棒的概率为( )
D
3.一个布袋里装有3 个红球和 5 个黄球,它们除颜色外其余都相同.从中任意摸出一个球是红球的概率是( )
4.书架上摆放5 本书,其中有 2 本教科书,3 本文学书,从书架上任意抽取 1 本,抽到教科书的概率是 ( )
C
C
5.一个小球在如图S6-1所示的地板上随意滚动,当小球停下时,最终停在地板上阴影部分的概率是( )
A
6.如图S6-2,一个正六边形转盘被分成6 个全等的正三角形.任意旋转这个转盘 1 次,当转盘停止转动时,指针指向阴影区域的概率是( )
D
7. 在一个不透明的盒子中装有红、白两种除颜色外完全相同的球,其中有a个白球和3个红球,若每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子.通过大量重复试验后,发现摸到红球的频率稳定在20%左右,则a的值约为( )
A. 9 B. 12 C. 15 D. 18
B
8.一枚质地均匀的正方体骰子,其六个面上分别刻有1,2,3,
4,5,6 的点数,掷这个骰子一次,则掷得面朝上的点数为奇数的概率是 ( )
C
9.小真煮好了25 颗汤圆,其中 15 颗为芝麻汤圆,10 颗为花生汤圆,已知小真想从煮好的汤圆中捞一颗,若每颗汤圆被小真捞到的机会相等,则他捞到花生汤圆的概率为 ( )
C
10.用频率估计概率,可以发现,抛掷一枚硬币,“正面朝上”的概率为0.5,是指( )
A. 连续掷 2 次,结果一定是“正面朝上”和“反面朝上”各 1 次
B. 连续抛掷 100 次,结果一定是“正面朝上”和“反面朝上”各 50 次
C. 抛掷 2n 次硬币,恰好有 n 次“正面朝上”
D. 抛掷 n 次,当 n 越来越大时,“正面朝上”的频率会越来越稳定于 0.5
D
摸球的次数n 100 200 300 500 800 1 000 1 500
摸到白球的次数m 70 128 171 302 481 599 903
0.70 0.64 0.57 0.604 0.601 0.599 0.602
11.在一个不透明的盒子里装着除颜色外完全相同的黑、白两种小球共40个.小颖做摸球试验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色后放回,不断重复上述过程,多次试验后,得到下表中的数据,并得出了四个结论,其中正确的是( )
B
A. 试验1 500 次摸到白球的频率比试验800次的更接近0.6
B. 从该盒子中任意摸出一个小球,摸到白球的频率约为0.6
C. 当试验次数n为2 000时,摸到白球的次数m一定等于1 200
D. 这个盒子中的白球一定有24个
12.某小组做“用频率估计概率”的试验时,统计了某一结果出现的频率,绘制了如图S6-3所示的折线统计图,则符合这一结果的试验最有可能的是( )
在“石头、剪刀、布”的游戏中,
小明随机出的是“剪刀”
B. 一副去掉大、小王的普通扑克牌洗
匀后,从中任抽一张牌的花色是红桃
C. 暗箱中有 1 个红球和 2 个黄球,
它们只有颜色上的区别,从中任取一球是黄球
D. 掷一个质地均匀的正六面体骰子,向上的面的点数是 4
D
二、填空题(本大题6小题,每小题4分,共24分)
13.一个袋中装有6 个红球,5 个黄球,3 个白球,每个球除颜色外都相同,任意摸出一球,摸到 球的可能性最大.
14.在一个箱子里放有1 个白球和 2 个红球,它们除颜色外其余都相同,从箱子里摸出 1 个球,则摸到红球的概率是 .
红
15.向如图S6-4所示的正三角形区域扔沙包(区域中每一个小正三角形除颜色外完全相同),假设沙包击中每一个小三角形是等可能的,扔沙包1 次击中阴影区域的概率等于 .
16. 把标有号码1,2,3,…,10的10个乒乓球放在一个箱子中,摇匀后,从中任意取一个,号码为小于7的奇数的概率是 .
17.一个不透明的袋子中装有除颜色外均相同的8 个黑球、 4 个白球和若干个红球.每次摇匀随机摸出一个球,记下颜色后再放回袋子中,通过大量重复摸球试验后,发现摸到红球的频率稳定于 0.4,由此可估计袋子中约有红球 个.
8
18.农业部门引进一批新麦种,在播种前做了五次发芽试验,目的是想了解一粒这样的麦种发芽情况,实验统计数据如下:
实验的麦种数/粒 500 500 500 500 500
发芽的麦种数/粒 492 487 491 493 489
发芽率/% 98.40 97.40 98.20 98.60 97.80
估计在与实验条件相同的情况下,种一粒这样的麦种发芽的概率约为 .(结果精确到0.01)
0.98
三、解答题(一)(本大题2小题,每小题8分,共16分)
19. 转动如图S6-5所示的转盘(转盘被等分成六份),转盘停止后,指针对着某一数字.
(1)“指针对着2”和“指针对着 1”哪个可能性大?
(2)“指针对着3”和“指针对着 1”哪个可能性大?
解:(1) “指针对着 2”和“指针对着 1”
的可能性相同.
(2) “指针对着1”的可能性大.
20.一个不透明的袋子中有 1 个红球,2 个绿球和 n 个白球,这些球除颜色外都相同.
(1)当n=1 时,从袋中随机摸出 1 个球,摸到红球和摸到白球的可能性 ;(填“相同”或“不相同”)
(2)从袋中随机摸出1 个球,记录其颜色,然后放回.大量重复该试验,发现摸到绿球的频率稳定于 0.2,求 n 的值.
解:(2) 由题意,得2÷0.2=10(个).
10-1-2=7(个).
所以n=7.
相同
四、解答题(二)(本大题2小题,每小题10分,共20分)
21.甲认为如图S6-6所示的A,B两转盘都只有两种颜色,分别转动指针,待指针停止后,指针不是停在红色上就是停在蓝色上,机会一样,都是 50%,你认为对吗?为什么?
解:不对.
因为A转盘上指针停在红色上的概率是 ,停在蓝色上的概率是
所以指针停在红色上和停在蓝色上的机会不一样.
因为B转盘上指针停在红色上的概率是 ,停在蓝色上的概率是 ,
所以指针停在红色上和停在蓝色上的机会一样.
22.某市民政部门今年五一期间举行了“即开式社会福利彩票”销售活动,设置彩票2 000万张(每张彩票 2 元).在这些彩票中,设置了如下的奖项.
奖金/万元 50 15 8 2 …
数量/个 10 20 20 180 …
(1)如果花2元购买1张彩票,那么能得到50万元大奖的概率是多少?
(2)如果花2元购买1张彩票,那么能得到8万元以上(包括8万元)大奖的概率是多少?
解:(1) 因为彩票2 000万张,50万元的彩票有10张,
所以能得到50万元大奖的概率是
(2)因为彩票 2 000 万张,8万元以上(包括 8 万元)的彩票有 10+20+20=50(张),
所以能得到8万以上(包括8万元)大奖的概率是
五、解答题(三)(本大题2小题,每小题12分,共24分)
23.如图S6-7,小林和小芳两人玩游戏,掷骰子定输赢.
(1)朝上一面点数是3 的倍数的情况有哪些?出现朝上一面点数是 3 的倍数的概率是多少?
(2)朝上一面点数不是3 的倍数的情况有哪些?出现朝上一面点数不是 3 的倍数的概率是多少?
(3)请你评判一下,这样的规则公平吗?
解:(1) 朝上一面点数是 3 的倍数的情况有 3,6 两种,
出现朝上一面点数是3 的倍数的概率为
(2) 朝上一面点数不是3 的倍数的情况有 1,2,4,5 四种,
出现朝上一面点数不是3 的倍数的概率为
(3) 出现朝上一面点数是3 的倍数的概率小于出现朝上一面点数不是 3 的倍数的概率,规则不公平.
24. 某批足球的质量检测结果如下:
抽取足球数n 100 200 400 600 800 1 000
合格的频数m 93 192 384 564 759 950
合格的频率 0.93 0.96 0.96 0.94
(1)填写表中的空格.(结果精确到0.01)
(2)请在图S6-8中画出合格的频率的折线统计图.
(3)从这批足球任意抽取的一只足球是合格品的概率估计值是多少?并说明理由.
0.95
0.95
解:(2) 如答图S6-1.
(3) 从这批足球任意抽取的一只足球是合格品的概率估计值是0.95.
因为从折线统计图中可知,随着试验次数的增大,频率逐渐稳定到常数0.95 附近,
所以从这批足球任意抽取的一只足球是合格品的概率估计值是0.95.
谢 谢
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
