沪科版数学七年级下册专题专练 微专题9 平行线的性质与判定(含答案)
文档属性
| 名称 | 沪科版数学七年级下册专题专练 微专题9 平行线的性质与判定(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-24 09:11:16 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
沪科版数学七年级下册专题专练
微专题9 平行线的性质与判定
一、选择题
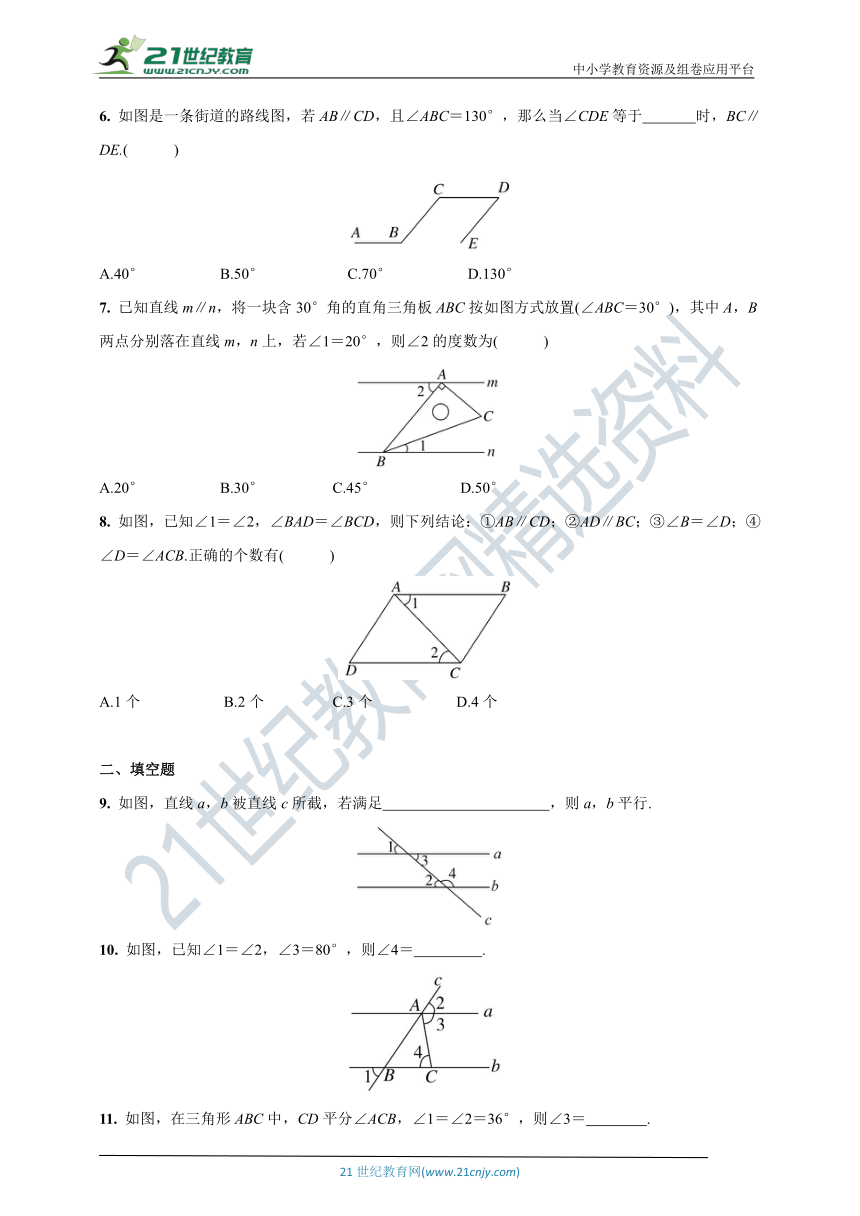
1. 如图,直线a∥b,c⊥a,则c与b相交所形成的∠2的度数为( )
A.45° B.60° C.90° D.120°
2. 如图,下列条件中,不能判断直线l1∥l2的是( )
A.∠1=∠3 B.∠2=∠3 C.∠4=∠5 D.∠2+∠4= 180°
3. 如图,若∠1=50°,∠C=50°,∠2=120°,则( )
A.∠B=40° B.∠B=50° C.∠B=60° D.∠B=120°
4. 如图,已知AB∥CD,∠DFE=135°,则∠ABE的度数为( )
A.30° B.45° C.60° D.90°
5. 如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C度数是( )
A.30° B.60° C.80° D. 120°
6. 如图是一条街道的路线图,若AB∥CD,且∠ABC=130°,那么当∠CDE等于 时,BC∥DE.( )
A.40° B.50° C.70° D.130°
7. 已知直线m∥n,将一块含30°角的直角三角板ABC按如图方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上,若∠1=20°,则∠2的度数为( )
A.20° B.30° C.45° D.50°
8. 如图,已知∠1=∠2,∠BAD=∠BCD,则下列结论:①AB∥CD;②AD∥BC;③∠B=∠D;④∠D=∠ACB.正确的个数有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
9. 如图,直线a,b被直线c所截,若满足 ,则a,b平行.
10. 如图,已知∠1=∠2,∠3=80°,则∠4= .
11. 如图,在三角形ABC中,CD平分∠ACB,∠1=∠2=36°,则∠3= .
12. 如图是一台起重机的工作简图,前后两次吊杆位置OP1,OP2与绳线的夹角分别是30°和70°,则吊杆前后两次的夹角∠P1OP2= .
13. 如图,BC∥DE,∠E+∠B=180°,则AB和EG的位置关系为 .
14. 如图,直线AB,CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3= .
三、解答题
15. 如图,AB∥DE,∠1=∠2,直线AE与DC平行吗 请说明理由.
16. 如图,已知点A,B,E共线,AD∥BC,∠1=∠2,∠A=100°,求∠C的度数.
17. 如图,已知DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2.
试说明:CD⊥AB.
解:因为DG⊥BC,AC⊥BC(已知),
所以∠DGB=∠ACB=90°(垂直的定义),
所以DG∥AC( ),
所以∠2=∠ ( ).
因为∠1=∠2(已知),
所以∠1=∠ (等量代换),
所以EF∥CD( ),
所以∠AEF=∠ ( ).
因为EF⊥AB(已知),
所以∠AEF=90°( ),
所以∠ADC=90°( ),
所以CD⊥AB( ).
18. 如图,已知∠1+∠2= 180°,∠DAE=∠BCF.
(1)试判断直线AE与CF有怎样的位置关系,并说明理由;
(2)若∠ BCF=70°,求∠ADF的度数.
19. 如图,AB∥CD,∠1=∠B,∠2=∠D.试说明:BE⊥DE.
参 考 答 案
1. C 2. B 3. C 4. B 5. A 6. B 7. D 8. C
9. ∠1=∠2(答案不唯一) 10. 80° 11. 72° 12. 40° 13. 平行 14. 80°
15. 解:AE∥DC. 理由如下:因为AB∥DE(已知),所以∠1=∠AED(两直线平行,内错角相等). 因为∠1=∠2(已知) ,所以∠2=∠AED(等量代换),所以AE∥DC(内错角相等,两直线平行).
16. 解:因为AD∥BC,∠A= 100°,所以∠CBE=∠A= 100°.因为∠1=∠2,所以CD∥AE,所以∠C=∠ CBE=100°.
17. 解:同位角相等,两直线平行 ACD 两直线平行,内错角相等 ACD 同位角相等,两直线平行 ADC 两直线平行,同位角相等 垂直的定义 等量代换 垂直的定义
18. 解:(1)AE∥CF. 理由如下:因为∠1+∠2=180°,∠BDC+∠2=180°,所以∠1=∠BDC,所以AE∥CF.
(2)由(1)可知AE∥CF,所以∠BCF=∠CBE. 因为∠DAE=∠BCF,所以∠DAE=∠CBE,所以AD∥BC,所以∠ADF=∠BCF=70°.
19. 解:如图,过点E作EF∥AB,则∠B=∠3.又因为∠1=∠B,所以∠1=∠3. 因为AB∥EF,AB∥CD,所以EF∥CD,所以∠4=∠D. 又因为∠2=∠D,所以∠2=∠4. 因为∠1+∠2+∠3+∠4=180°,所以∠3+∠4=90°,即∠BED=90°,所以BE⊥ED.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
沪科版数学七年级下册专题专练
微专题9 平行线的性质与判定
一、选择题
1. 如图,直线a∥b,c⊥a,则c与b相交所形成的∠2的度数为( )
A.45° B.60° C.90° D.120°
2. 如图,下列条件中,不能判断直线l1∥l2的是( )
A.∠1=∠3 B.∠2=∠3 C.∠4=∠5 D.∠2+∠4= 180°
3. 如图,若∠1=50°,∠C=50°,∠2=120°,则( )
A.∠B=40° B.∠B=50° C.∠B=60° D.∠B=120°
4. 如图,已知AB∥CD,∠DFE=135°,则∠ABE的度数为( )
A.30° B.45° C.60° D.90°
5. 如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C度数是( )
A.30° B.60° C.80° D. 120°
6. 如图是一条街道的路线图,若AB∥CD,且∠ABC=130°,那么当∠CDE等于 时,BC∥DE.( )
A.40° B.50° C.70° D.130°
7. 已知直线m∥n,将一块含30°角的直角三角板ABC按如图方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上,若∠1=20°,则∠2的度数为( )
A.20° B.30° C.45° D.50°
8. 如图,已知∠1=∠2,∠BAD=∠BCD,则下列结论:①AB∥CD;②AD∥BC;③∠B=∠D;④∠D=∠ACB.正确的个数有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
9. 如图,直线a,b被直线c所截,若满足 ,则a,b平行.
10. 如图,已知∠1=∠2,∠3=80°,则∠4= .
11. 如图,在三角形ABC中,CD平分∠ACB,∠1=∠2=36°,则∠3= .
12. 如图是一台起重机的工作简图,前后两次吊杆位置OP1,OP2与绳线的夹角分别是30°和70°,则吊杆前后两次的夹角∠P1OP2= .
13. 如图,BC∥DE,∠E+∠B=180°,则AB和EG的位置关系为 .
14. 如图,直线AB,CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3= .
三、解答题
15. 如图,AB∥DE,∠1=∠2,直线AE与DC平行吗 请说明理由.
16. 如图,已知点A,B,E共线,AD∥BC,∠1=∠2,∠A=100°,求∠C的度数.
17. 如图,已知DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2.
试说明:CD⊥AB.
解:因为DG⊥BC,AC⊥BC(已知),
所以∠DGB=∠ACB=90°(垂直的定义),
所以DG∥AC( ),
所以∠2=∠ ( ).
因为∠1=∠2(已知),
所以∠1=∠ (等量代换),
所以EF∥CD( ),
所以∠AEF=∠ ( ).
因为EF⊥AB(已知),
所以∠AEF=90°( ),
所以∠ADC=90°( ),
所以CD⊥AB( ).
18. 如图,已知∠1+∠2= 180°,∠DAE=∠BCF.
(1)试判断直线AE与CF有怎样的位置关系,并说明理由;
(2)若∠ BCF=70°,求∠ADF的度数.
19. 如图,AB∥CD,∠1=∠B,∠2=∠D.试说明:BE⊥DE.
参 考 答 案
1. C 2. B 3. C 4. B 5. A 6. B 7. D 8. C
9. ∠1=∠2(答案不唯一) 10. 80° 11. 72° 12. 40° 13. 平行 14. 80°
15. 解:AE∥DC. 理由如下:因为AB∥DE(已知),所以∠1=∠AED(两直线平行,内错角相等). 因为∠1=∠2(已知) ,所以∠2=∠AED(等量代换),所以AE∥DC(内错角相等,两直线平行).
16. 解:因为AD∥BC,∠A= 100°,所以∠CBE=∠A= 100°.因为∠1=∠2,所以CD∥AE,所以∠C=∠ CBE=100°.
17. 解:同位角相等,两直线平行 ACD 两直线平行,内错角相等 ACD 同位角相等,两直线平行 ADC 两直线平行,同位角相等 垂直的定义 等量代换 垂直的定义
18. 解:(1)AE∥CF. 理由如下:因为∠1+∠2=180°,∠BDC+∠2=180°,所以∠1=∠BDC,所以AE∥CF.
(2)由(1)可知AE∥CF,所以∠BCF=∠CBE. 因为∠DAE=∠BCF,所以∠DAE=∠CBE,所以AD∥BC,所以∠ADF=∠BCF=70°.
19. 解:如图,过点E作EF∥AB,则∠B=∠3.又因为∠1=∠B,所以∠1=∠3. 因为AB∥EF,AB∥CD,所以EF∥CD,所以∠4=∠D. 又因为∠2=∠D,所以∠2=∠4. 因为∠1+∠2+∠3+∠4=180°,所以∠3+∠4=90°,即∠BED=90°,所以BE⊥ED.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
