七年级下册数学第十章数据的收集、整理与描述单元测试(B)(附答案解析)
文档属性
| 名称 | 七年级下册数学第十章数据的收集、整理与描述单元测试(B)(附答案解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 747.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-07 00:00:00 | ||
图片预览


文档简介
第十章数据的收集、整理与描述单元测试(B)
考试时间:100分钟;命题人:张洪峰
学校:___________姓名:___________班级:___________考号:___________
一.选择题(共10小题)
1.下表为某公司200名职员年龄的次数分配表,其中36~42岁及50~56岁的次数因污损而无法看出.若36~42岁及50~56岁职员人数的相对次数分别为a%、b%,则a+b之值为何?( )
年龄
22~28
29~35
36~42
43~49
50~56
57~63
次数
6
40
42
2
A.10 B.45 C.55 D.99
2.下列调查方式,你认为最合适的是( )
A.日光灯管厂要检测一批灯管的使用寿命,采用普查方式
B.了解衢州市每天的流动人口数,采用抽查方式
C.了解衢州市居民日平均用水量,采用普查方式
D.旅客上飞机前的安检,采用抽样调查方式
3.为了了解攀枝花市2012年中考数学学科各分数段成绩分布情况,从中抽取150名考生的中考数学成绩进行统计分析.在这个问题中,样本是指( )
A.150 B.被抽取的150名考生
C.被抽取的150名考生的中考数学成绩D.攀枝花市2012年中考数学成绩
4.下列调查:
①调查一批灯泡的使用寿命;
②调查全班同学的身高;
③调查市场上某种食品的色素含量是否符合国家标准;
④企业招聘,对应聘人员进行面试.
其中符合用抽样调查的是( )
A.①② B.①③ C.②④D.②③
5.某同学为了解梅州市火车站今年“五一”期间每天乘车人数,随机抽查了其中五天的乘车人数,所抽查的这五天中每天乘车人数是这个问题的( )
A.总体 B.个体 C.样本 D.以上都不对
6.下列调查中,适宜采用全面调查(普查)方式的是( )
A.对一批圆珠笔使用寿命的调查
B.对全国九年级学生身高现状的调查
C.对某品牌烟花爆竹燃放安全的调查
D.对一枚用于发射卫星的运载火箭各零部件的检查
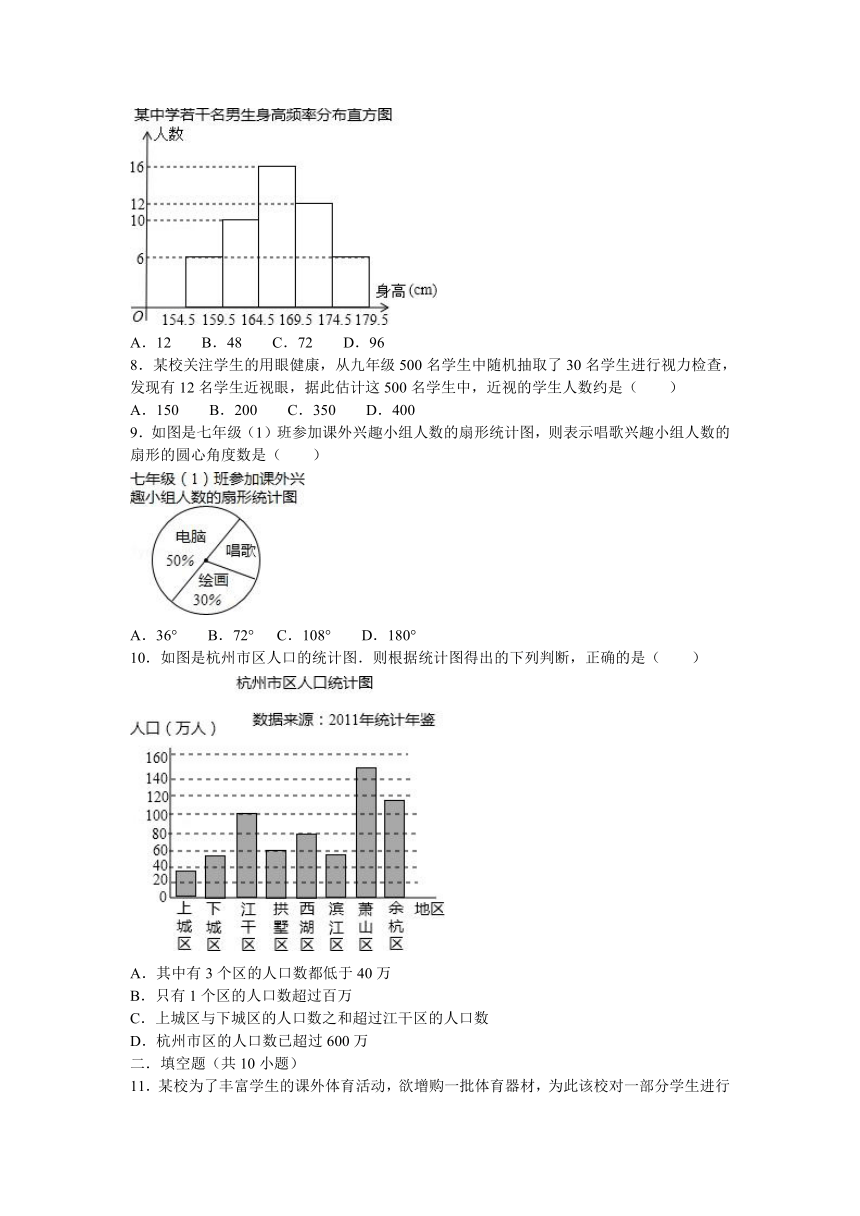
7.为了解中学300名男生的身高情况,随机抽取若干名男生进行身高测量,将所得数据整理后,画出频数分布直方图(如图).估计该校男生的身高在169.5cm~174.5cm之间的人数有( )
A.12 B.48 C.72 D.96
8.某校关注学生的用眼健康,从九年级500名学生中随机抽取了30名学生进行视力检查,发现有12名学生近视眼,据此估计这500名学生中,近视的学生人数约是( )
A.150 B.200 C.350 D.400
9.如图是七年级(1)班参加课外兴趣小组人数的扇形统计图,则表示唱歌兴趣小组人数的扇形的圆心角度数是( )
A.36° B.72° C.108° D.180°
10.如图是杭州市区人口的统计图.则根据统计图得出的下列判断,正确的是( )
A.其中有3个区的人口数都低于40万
B.只有1个区的人口数超过百万
C.上城区与下城区的人口数之和超过江干区的人口数
D.杭州市区的人口数已超过600万
二.填空题(共10小题)
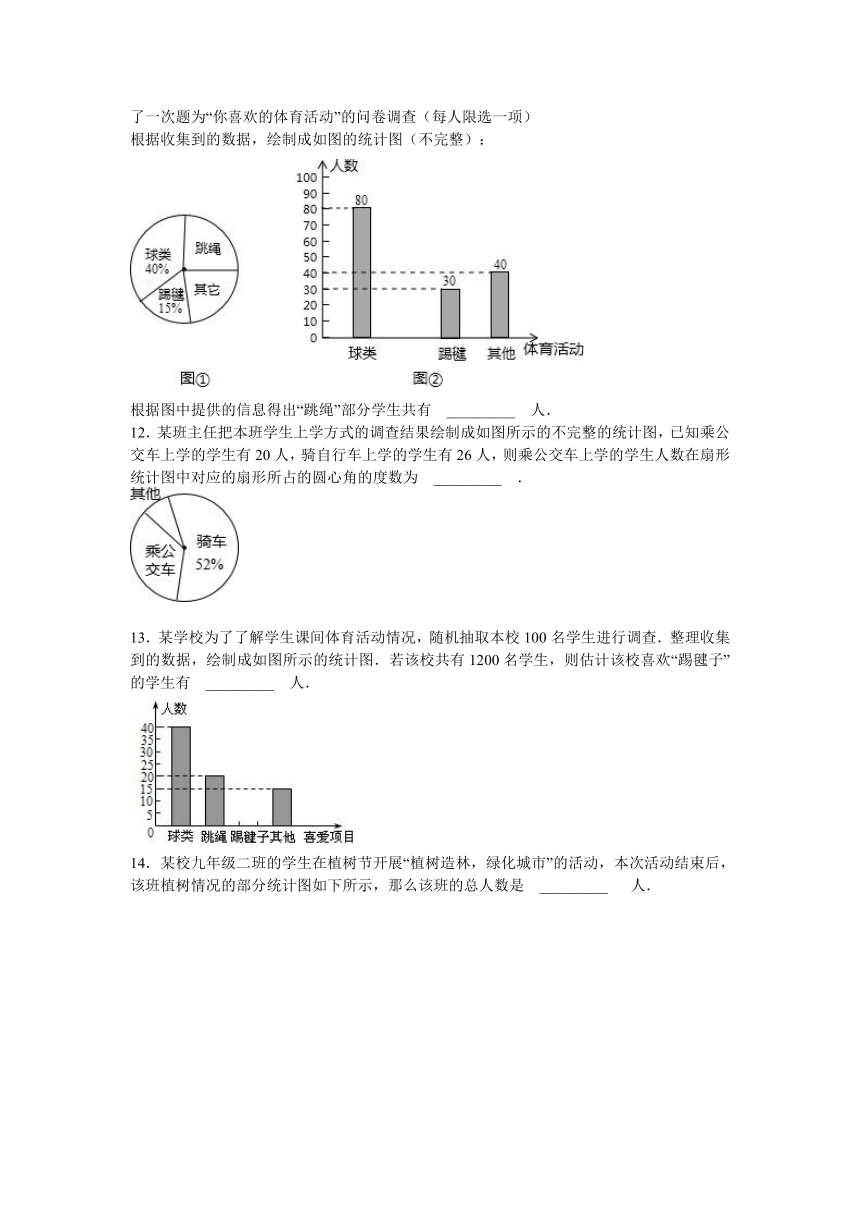
11.某校为了丰富学生的课外体育活动,欲增购一批体育器材,为此该校对一部分学生进行了一次题为“你喜欢的体育活动”的问卷调查(每人限选一项)
根据收集到的数据,绘制成如图的统计图(不完整):
根据图中提供的信息得出“跳绳”部分学生共有 _________ 人.
12.某班主任把本班学生上学方式的调查结果绘制成如图所示的不完整的统计图,已知乘公交车上学的学生有20人,骑自行车上学的学生有26人,则乘公交车上学的学生人数在扇形统计图中对应的扇形所占的圆心角的度数为 _________ .
13.某学校为了了解学生课间体育活动情况,随机抽取本校100名学生进行调查.整理收集到的数据,绘制成如图所示的统计图.若该校共有1200名学生,则估计该校喜欢“踢毽子”的学生有 _________ 人.
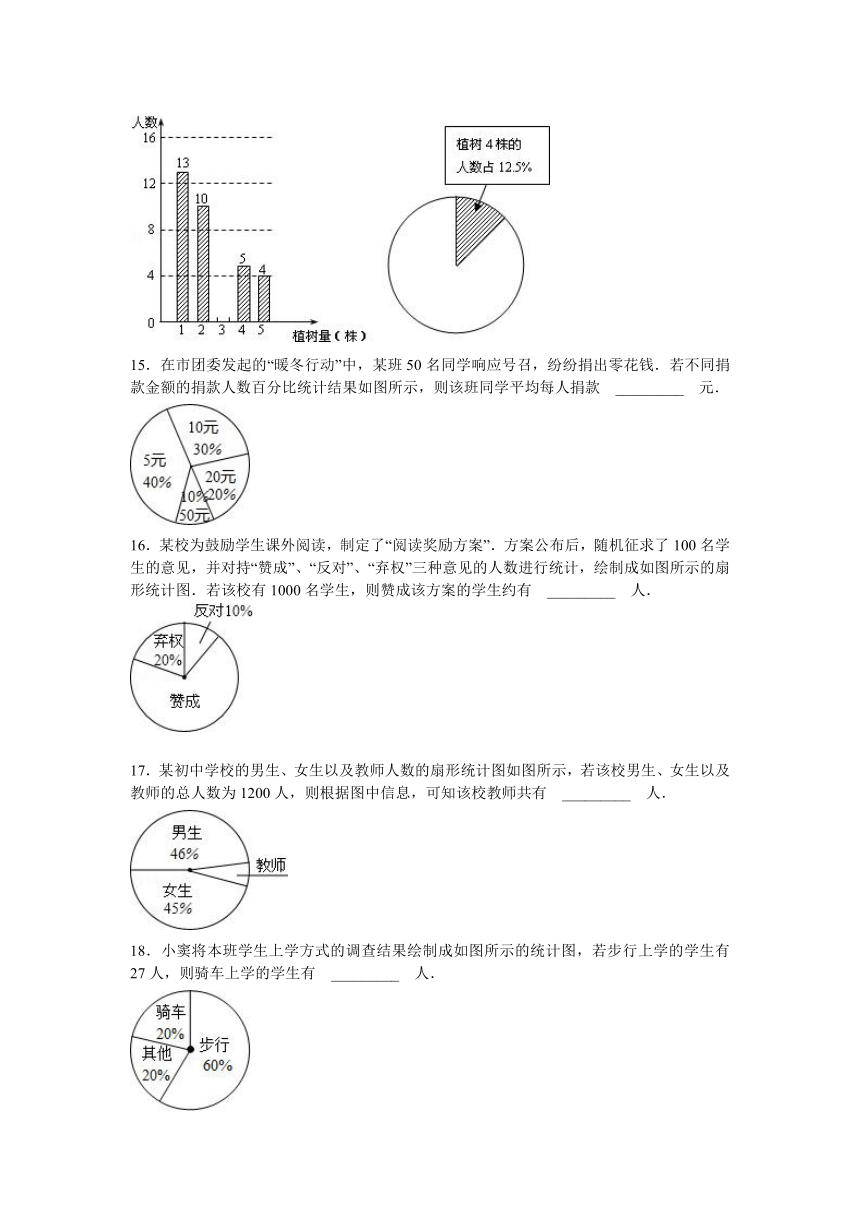
14.某校九年级二班的学生在植树节开展“植树造林,绿化城市”的活动,本次活动结束后,该班植树情况的部分统计图如下所示,那么该班的总人数是 _________ 人.
15.在市团委发起的“暖冬行动”中,某班50名同学响应号召,纷纷捐出零花钱.若不同捐款金额的捐款人数百分比统计结果如图所示,则该班同学平均每人捐款 _________ 元.
16.某校为鼓励学生课外阅读,制定了“阅读奖励方案”.方案公布后,随机征求了100名学生的意见,并对持“赞成”、“反对”、“弃权”三种意见的人数进行统计,绘制成如图所示的扇形统计图.若该校有1000名学生,则赞成该方案的学生约有 _________ 人.
17.某初中学校的男生、女生以及教师人数的扇形统计图如图所示,若该校男生、女生以及教师的总人数为1200人,则根据图中信息,可知该校教师共有 _________ 人.
18.小窦将本班学生上学方式的调查结果绘制成如图所示的统计图,若步行上学的学生有27人,则骑车上学的学生有 _________ 人.
19.生物工作者为了估计一片山林中雀鸟的数量,设计了如下方案:先捕捉100只雀鸟,给它们做上标记后放回山林;一段时间后,再从中随机捕捉500只,其中有标记的雀鸟有5只.请你帮助工作人员估计这片山林中雀鸟的数量约为 _________ 只.
20.某班总人数为50人,根据全班学生的课外活动情况绘制的统计图如右图,长跑的人数占30%,跳高的人数占50%,那么参加其他活动的人数为 _________ 人.
三.解答题(共9小题)
21.扬州市中小学全面开展“体艺2+1”活动,某校根据学校实际,决定开设A:篮球,B:乒乓球,C:声乐,D:健美操等四中活动项目,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制了两幅不完整的统计图.请回答下列问题:
(1)这次被调查的学生共有 _________ 人.
(2)请你将统计图1补充完整.
(3)统计图2中D项目对应的扇形的圆心角是 _________ 度.
(4)已知该校学生2400人,请根据调查结果估计该校最喜欢乒乓球的学生人数.
22.第三十届夏季奥林匹克运动会将于2012年7月27日至8月12日在英国伦敦举行,目前正在进行火炬传递活动.某校学生会为了确定近期宣传专刊的主题,想知道学生对伦敦奥运会火炬传递路线的了解程度,决定随机抽取部分学生进行一次问卷调查,并根据收集到的信息进行了统计,绘制了如图两幅上不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有 _________ 名;
(2)请补全折线统计图,并求出扇形统计图中“基本了解”部分所对应扇形的圆心角的大小;
(3)若该校共有1200名学生,请根据上述调查结果估计该校学生中对伦敦奥运火炬传递路线达到了“了解”和“基本了解”程度的总人数.
23.某市园林处去年植树节在滨海路两侧栽了A,B,C三个品种的树苗.栽种的A,B,C三个品种树苗数量的扇形统计图如图(1),其中B种树苗数量对应的扇形圆心角为120°.今年植树节前管理员调查了这三个品种树苗的成活率情况,准备今年从三个品种中选成活率最高的品种再进行栽种.经调查得知:A品种的成活率为85%,三个品种的总成活率为89%,但三个品种树苗成活数量统计图尚不完整,如图(2).
请你根据以上信息帮管理员解决下列问题:
(1)三个品种树苗去年共栽多少棵?
(2)补全条形统计图,并通过计算,说明今年应栽哪个品种的树苗.
24. 2011年徐州市全年实现地区生产总值3551.65亿元,按可比价格计算,比上年增长13.5%,经济平稳较快增长.其中,第一产业、第二产业、第三产业增加值与增长率情况如图所示:
根据图中信息,写成下列填空:
(1)第三产业的增加值为 _________ 亿元:
(2)第三产业的增长率是第一产业增长率的 _________ 倍(精确到0.1);
(3)三个产业中第 _________ 产业的增长最快.
25.为了推动课堂教学改革,打造高效课堂,配合我市“两型课堂”的课题研究,莲城中学对八年级部分学生就一期来“分组合作学习”方式的支持程度进行调查,统计情况如图.试根据图中提供的信息,回答下列问题:
(1)求本次被调查的八年级学生的人数,并补全条形统计图;
(2)若该校八年级学生共有180人,请你估计该校八年级有多少名学生支持“分组合作学习”方式(含“非常喜欢”和“喜欢”两种情况的学生)?
26.某市青少年宫准备在七月一日组织市区部分学校的中小学生到本市A,B,C,D,E五个红色旅游景区“一日游”,每名学生只能在五个景区中任选一个.为估算到各景区旅游的人数,青少年宫随机抽取这些学校的部分学生,进行了“五个红色景区,你最想去哪里”的问卷调查,在统计了所有的调查问卷后将结果绘制成如图所示的统计图.
(1)求参加问卷调查的学生数,并将条形统计图补充完整;
(2)若参加“一日游”的学生为1000人,请估计到C景区旅游的人数.
27.某市为提高学生参与体育活动的积极性,2011年9月围绕“你最喜欢的体育运动项目(只写一项)”这一问题,对初一新生进行随机抽样调查,下图是根据调查结果绘制成的统计图(不完整).
请你根据图中提供的信息解答下列问题:
(1)本次抽样调查的样本容量是多少?
(2)根据条形统计图中的数据,求扇形统计图中“最喜欢足球运动”的学生数所对应扇形的圆心角度数.
(3)请将条形统计图补充完整.
(4)若该市2011年约有初一新生21000人,请你估计全市本届学生中“最喜欢足球运动”的学生约有多少人.
28.某校组织学生书法比赛,对参赛作品按A、B、C、D四个等级进行了评定.现随机抽取部分学生书法作品的评定结果进行分析,并绘制扇形统计图和条形统计图如下:
根据上述信息完成下列问题:
(1)求这次抽取的样本的容量;
(2)请在图②中把条形统计图补充完整;
(3)已知该校这次活动共收到参赛作品750份,请你估计参赛作品达到B级以上(即A级和B级)有多少份?
29.某地为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好地决策,自来水公司随机抽取部分用户的用适量数据,并绘制了如下不完整统计图(每组数据包括右端点但不包括左端点),请你根据统计图解决下列问题:
(1)此次调查抽取了多少用户的用水量数据?
(2)补全频数分布直方图,求扇形统计图中“25吨~30吨”部分的圆心角度数;
(3)如果自来水公司将基本用水量定为每户25吨,那么该地20万用户中约有多少用户的用水全部享受基本价格?
参考答案与试题解析
一.选择题(共10小题)
1.解答:
解:由表知36~42岁及50~56岁的职员人数共有,
200﹣6﹣40﹣42﹣2=110人,
所以,a%+b%=×100%=55%,
所以a+b=55.
故选C.
2.解答:
解:A.日光灯管厂要检测一批灯管的使用寿命,应采用抽样调查方式,故此选项错误;
B.了解衢州市每天的流动人口数,采用抽查方式;故此选项正确;
C.了解衢州市居民日平均用水量,应采用抽样调查方式;故此选项错误;
D.旅客上飞机前的安检,应采用全面调查方式;故此选项错误.
故选:B.
3.解答:
解:了解攀枝花市2012年中考数学学科各分数段成绩分布情况,从中抽取150名考生的中考数学成绩进行统计分析.
样本是,被抽取的150名考生的中考数学成绩,
故选C.
4.解答:
解:①调查一批灯泡的使用寿命,适合抽样调查;
②调查全班同学的身高,适合全面调查;
③调查市场上某种食品的色素含量是否符合国家标准,适合抽样调查;
④企业招聘,对应聘人员进行面试,适合全面调查;
故选B.
5.解答:
解:∵抽查的是“五一”期间每天乘车人数,
∴“五一”期间每天乘车人数是个体.
故选B.
6.解答:
解:A、对一批圆珠笔使用寿命的调查,由于具有破坏性,应当使用抽样调查,故本选项错误;
B、对全国九年级学生身高现状的调查,人数太多,不便于测量,应当采用抽样调查,故本选项错误;
C、对某品牌烟花爆竹燃放安全的调查,由于具有破坏性,应当使用抽样调查,故本选项错误;
D、对一枚用于发射卫星的运载火箭各零部件的检查,只有做到全面调查才能做到准确无误,故必须全面调查,故此选项正确.
故选:D.
7.解答:
解:根据图形,身高在169.5cm~174.5cm之间的人数的百分比为:
×100%=24%,
所以,该校男生的身高在169.5cm~174.5cm之间的人数有300×24%=72(人).
故选C.
8.解答:
解:500×=200人,
即近视的学生人数约200人.
故选B.
9.解答:
解:唱歌所占百分数为:1﹣50%﹣30%=20%,
唱歌兴趣小组人数的扇形的圆心角度数为:360°×20%=72°.
故选B.
10.解答:
解:A、只有上城区人口数都低于40万,故此选项错误;
B、萧山区、余杭区两个区的人口超过100万,故此选项错误;
C、上城区与下城区的人口数之和低于江干区的人口数,故此选项错误;
D、杭州市区的人口数已超过600万,故此选项正确;
故选:D.
二.填空题(共10小题)
11.某校为了丰富学生的课外体育活动,欲增购一批体育器材,为此该校对一部分学生进行了一次题为“你喜欢的体育活动”的问卷调查(每人限选一项)
根据收集到的数据,绘制成如图的统计图(不完整):
根据图中提供的信息得出“跳绳”部分学生共有 50 人.
解答:
解:∵从条形统计图知喜欢球类的有80人,占40%
∴总人数为80÷40%=200人
∴喜欢跳绳的有200﹣80﹣30﹣40=50人,
故答案为50.
12.某班主任把本班学生上学方式的调查结果绘制成如图所示的不完整的统计图,已知乘公交车上学的学生有20人,骑自行车上学的学生有26人,则乘公交车上学的学生人数在扇形统计图中对应的扇形所占的圆心角的度数为 144° .
解答:
解:根据题意得:
总人数是:26÷52%=50人,
所以乘车部分所对应的圆心角的度数为360×=144°;
故答案为:144°.
13.某学校为了了解学生课间体育活动情况,随机抽取本校100名学生进行调查.整理收集到的数据,绘制成如图所示的统计图.若该校共有1200名学生,则估计该校喜欢“踢毽子”的学生有 300 人.
解答:
解:∵随机抽取本校的100名学生中喜欢“踢毽子”的学生有:100﹣40﹣20﹣15=25(人),
∴喜欢“踢毽子”的频率为:25÷100=0.25,
∴该校喜欢“踢毽子”的学生有:1200×0.25=300(人).
故答案为:300.
14.某校九年级二班的学生在植树节开展“植树造林,绿化城市”的活动,本次活动结束后,该班植树情况的部分统计图如下所示,那么该班的总人数是 40 人.
解答:
解:∵植树4株的人数为5人,占总人数的12.5%,
∴该班的总人数=5÷12.5%=40(人).
故答案为40.
15.在资阳市团委发起的“暖冬行动”中,某班50名同学响应号召,纷纷捐出零花钱.若不同捐款金额的捐款人数百分比统计结果如图所示,则该班同学平均每人捐款 14 元.
解答:
解:该班同学平均每人捐款:10×30%+20×20%+50×10%+5×40%=14元.
故答案为14.
16.某校为鼓励学生课外阅读,制定了“阅读奖励方案”.方案公布后,随机征求了100名学生的意见,并对持“赞成”、“反对”、“弃权”三种意见的人数进行统计,绘制成如图所示的扇形统计图.若该校有1000名学生,则赞成该方案的学生约有 700 人.
解答:
解:由扇形统计图可知赞成的百分比为:1﹣20%﹣10%=70%
∴1000名学生中赞成该方案的学生约有1000×70%=700人.
故答案为:700.
17.某初中学校的男生、女生以及教师人数的扇形统计图如图所示,若该校男生、女生以及教师的总人数为1200人,则根据图中信息,可知该校教师共有 108 人.
解答:
解:教师所占的百分比是:1﹣46%﹣45%=9%,
则教师的人数是:1200×9%=108.
故答案是:108.
18.小窦将本班学生上学方式的调查结果绘制成如图所示的统计图,若步行上学的学生有27人,则骑车上学的学生有 9 人.
解答:
解:由图可知步行上学的学生占本班学生上学方式的60%,又知步行上学的学生有27人,
∴本班学生总数=27÷60%=45人,
由图可知骑车的占20%,
∴骑车上学的学生=45×20%=9人.
故答案为9.
19.生物工作者为了估计一片山林中雀鸟的数量,设计了如下方案:先捕捉100只雀鸟,给它们做上标记后放回山林;一段时间后,再从中随机捕捉500只,其中有标记的雀鸟有5只.请你帮助工作人员估计这片山林中雀鸟的数量约为 10000 只.
解答:
解:100=10000只.
故答案为:10000. 20.某班总人数为50人,根据全班学生的课外活动情况绘制的统计图如右图,长跑的人数占30%,跳高的人数占50%,那么参加其他活动的人数为 10 人.
解答:
解:由扇形图知,参加其他活动的人数占全班总人数的百分比为:1﹣30%﹣50%=20%,
又知某班总人数为50人,
∴参加其他活动的人数为 50×20%=10人,
三.解答题(共9小题)
21.扬州市中小学全面开展“体艺2+1”活动,某校根据学校实际,决定开设A:篮球,B:乒乓球,C:声乐,D:健美操等四中活动项目,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制了两幅不完整的统计图.请回答下列问题:
(1)这次被调查的学生共有 200 人.
(2)请你将统计图1补充完整.
(3)统计图2中D项目对应的扇形的圆心角是 72 度.
(4)已知该校学生2400人,请根据调查结果估计该校最喜欢乒乓球的学生人数.
解答:
解:(1)根据喜欢篮球的人数为20人,所占百分比为10%,
故这次被调查的学生共有:20÷10%=200;
故答案为:200;
(2)根据喜欢C音乐的人数=200﹣20﹣80﹣40=60,
故C对应60人,如图所示:
(3)根据喜欢D:健美操的人数为:40人,
则统计图2中D项目对应的扇形的圆心角是:40÷200×360°=72°;
故答案为:72;
(4)根据样本中最喜欢乒乓球的学生人数为80人,
故该校学生2400人中最喜欢乒乓球的学生人数为:×2400=960人.
答:该校最喜欢乒乓球的学生人数大约为960人.
22.第三十届夏季奥林匹克运动会将于2012年7月27日至8月12日在英国伦敦举行,目前正在进行火炬传递活动.某校学生会为了确定近期宣传专刊的主题,想知道学生对伦敦奥运会火炬传递路线的了解程度,决定随机抽取部分学生进行一次问卷调查,并根据收集到的信息进行了统计,绘制了如图两幅上不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有 60 名;
(2)请补全折线统计图,并求出扇形统计图中“基本了解”部分所对应扇形的圆心角的大小;
(3)若该校共有1200名学生,请根据上述调查结果估计该校学生中对伦敦奥运火炬传递路线达到了“了解”和“基本了解”程度的总人数.
解答:
解:(1)根据题意得:30÷50%=60(名)
答:接受问卷调查的学生共有 60名;
(2)如图:60﹣10﹣15﹣30=5(名);
“基本了解”部分所对应扇形的圆心角是:360°×=90°;
(3)该校学生中对伦敦奥运火炬传递路线达到了“了解”和“基本了解”程度的总人数是:
1200×=400(名).
故答案为:60.
23.某市园林处去年植树节在滨海路两侧栽了A,B,C三个品种的树苗.栽种的A,B,C三个品种树苗数量的扇形统计图如图(1),其中B种树苗数量对应的扇形圆心角为120°.今年植树节前管理员调查了这三个品种树苗的成活率情况,准备今年从三个品种中选成活率最高的品种再进行栽种.经调查得知:A品种的成活率为85%,三个品种的总成活率为89%,但三个品种树苗成活数量统计图尚不完整,如图(2).
请你根据以上信息帮管理员解决下列问题:
(1)三个品种树苗去年共栽多少棵?
(2)补全条形统计图,并通过计算,说明今年应栽哪个品种的树苗.
解答:
解:(1)A品种树苗棵数为1020÷85%=1200(棵),
所以,三个品种树苗共栽棵数为1200÷40%=3000(棵);
(2)B品种树苗成活棵数为
3000×89%﹣1020﹣720=930(棵),
补全条形统计图,如图,…(7分)?
B品种树苗成活率为×100%=93%;
C品种树苗成活率为×100%=×100%=90%.
所以,B品种成活率最高,今年应栽B品种树苗.
24. 2011年徐州市全年实现地区生产总值3551.65亿元,按可比价格计算,比上年增长13.5%,经济平稳较快增长.其中,第一产业、第二产业、第三产业增加值与增长率情况如图所示:
根据图中信息,写成下列填空:
(1)第三产业的增加值为 1440.06 亿元:
(2)第三产业的增长率是第一产业增长率的 3.2 倍(精确到0.1);
(3)三个产业中第 二 产业的增长最快.
解答:
解:(1)由左图可知,第三产业的增加值为1440.06亿元,
故答案为:1440.06;
(2)由右图可知,14.50%÷4.50%≈3.2,
故答案为:3.2;
(3)由右图可知,三个产业的增长率依次为:4.50%,14.60%,14.50%,
由此可知,三个产业中第二产业的增长最快,
故答案为:二.
25.为了推动课堂教学改革,打造高效课堂,配合我市“两型课堂”的课题研究,莲城中学对八年级部分学生就一期来“分组合作学习”方式的支持程度进行调查,统计情况如图.试根据图中提供的信息,回答下列问题:
(1)求本次被调查的八年级学生的人数,并补全条形统计图;
(2)若该校八年级学生共有180人,请你估计该校八年级有多少名学生支持“分组合作学习”方式(含“非常喜欢”和“喜欢”两种情况的学生)?
解答:
解:(1)∵喜欢“分组合作学习”方式的圆心角度数为120°,频数为18,
∴喜欢“分组合作学习”方式的总人数为:18÷=54人,
故非常喜欢“分组合作学习”方式的人数为:54﹣18﹣6=30人,如图所示补全条形图即可;
(2)∵“非常喜欢”和“喜欢”两种情况在扇形统计图中所占圆心角为:120°+200°=320°,
∴支持“分组合作学习”方式所占百分比为:×100%,
∴该校八年级学生共有180人,有180×=160名学生支持“分组合作学习”方式.
26.某市青少年宫准备在七月一日组织市区部分学校的中小学生到本市A,B,C,D,E五个红色旅游景区“一日游”,每名学生只能在五个景区中任选一个.为估算到各景区旅游的人数,青少年宫随机抽取这些学校的部分学生,进行了“五个红色景区,你最想去哪里”的问卷调查,在统计了所有的调查问卷后将结果绘制成如图所示的统计图.
(1)求参加问卷调查的学生数,并将条形统计图补充完整;
(2)若参加“一日游”的学生为1000人,请估计到C景区旅游的人数.
解答:
解:(1)50÷25%=200(人),
到B景区旅游的人数是:
200﹣20﹣70﹣10﹣50=50(人),
(2)70÷200=35%,
1000×35%=350(人),
答:估计到C景区旅游的有350人.
27.某市为提高学生参与体育活动的积极性,2011年9月围绕“你最喜欢的体育运动项目(只写一项)”这一问题,对初一新生进行随机抽样调查,下图是根据调查结果绘制成的统计图(不完整).
请你根据图中提供的信息解答下列问题:
(1)本次抽样调查的样本容量是多少?
(2)根据条形统计图中的数据,求扇形统计图中“最喜欢足球运动”的学生数所对应扇形的圆心角度数.
(3)请将条形统计图补充完整.
(4)若该市2011年约有初一新生21000人,请你估计全市本届学生中“最喜欢足球运动”的学生约有多少人.
解答:
解:(1)100÷20%=500,
∴本次抽样调查的样本容量是500;
(2)∵360°×=43.2°,
∴扇形统计图中“最喜欢足球运动”的学生数所对应的扇形圆心角度数为43.2°;
(3)如图:
(4)21000×=2520(人)
全市本届学生中“最喜欢足球运动”的学生约有2520人;
28.某校组织学生书法比赛,对参赛作品按A、B、C、D四个等级进行了评定.现随机抽取部分学生书法作品的评定结果进行分析,并绘制扇形统计图和条形统计图如下:
根据上述信息完成下列问题:
(1)求这次抽取的样本的容量;
(2)请在图②中把条形统计图补充完整;
(3)已知该校这次活动共收到参赛作品750份,请你估计参赛作品达到B级以上(即A级和B级)有多少份?
解答:
解:(1)∵A级人数为24人,在扇形图中所占比例为20%,
∴这次抽取的样本的容量为:24÷20%=120;
(2)根据C级在扇形图中所占比例为30%,
得出C级人数为:120×30%=36人,
∴D级人数为:120﹣36﹣24﹣48=12人,
如图所示:
(3)∵A级和B级作品在样本中所占比例为:(24+48)÷120×100%=60%,
∴该校这次活动共收到参赛作品750份,参赛作品达到B级以上有750×60%=450份.
29.某地为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好地决策,自来水公司随机抽取部分用户的用适量数据,并绘制了如下不完整统计图(每组数据包括右端点但不包括左端点),请你根据统计图解决下列问题:
(1)此次调查抽取了多少用户的用水量数据?
(2)补全频数分布直方图,求扇形统计图中“25吨~30吨”部分的圆心角度数;
(3)如果自来水公司将基本用水量定为每户25吨,那么该地20万用户中约有多少用户的用水全部享受基本价格?
解答:
解:(1)10÷10%=100(户);
(2)100﹣10﹣36﹣25﹣9=100﹣80=20户,画直方图如图,
(画图正确没标记数字同样给分,算出“15﹣﹣20吨”部分的用户数是20但没画图给1分)
×360°=90°;
(3)×20=13.2(万户).
答:该地20万用户中约有13.2万户居民的用水全部享受基本价格.
考试时间:100分钟;命题人:张洪峰
学校:___________姓名:___________班级:___________考号:___________
一.选择题(共10小题)
1.下表为某公司200名职员年龄的次数分配表,其中36~42岁及50~56岁的次数因污损而无法看出.若36~42岁及50~56岁职员人数的相对次数分别为a%、b%,则a+b之值为何?( )
年龄
22~28
29~35
36~42
43~49
50~56
57~63
次数
6
40
42
2
A.10 B.45 C.55 D.99
2.下列调查方式,你认为最合适的是( )
A.日光灯管厂要检测一批灯管的使用寿命,采用普查方式
B.了解衢州市每天的流动人口数,采用抽查方式
C.了解衢州市居民日平均用水量,采用普查方式
D.旅客上飞机前的安检,采用抽样调查方式
3.为了了解攀枝花市2012年中考数学学科各分数段成绩分布情况,从中抽取150名考生的中考数学成绩进行统计分析.在这个问题中,样本是指( )
A.150 B.被抽取的150名考生
C.被抽取的150名考生的中考数学成绩D.攀枝花市2012年中考数学成绩
4.下列调查:
①调查一批灯泡的使用寿命;
②调查全班同学的身高;
③调查市场上某种食品的色素含量是否符合国家标准;
④企业招聘,对应聘人员进行面试.
其中符合用抽样调查的是( )
A.①② B.①③ C.②④D.②③
5.某同学为了解梅州市火车站今年“五一”期间每天乘车人数,随机抽查了其中五天的乘车人数,所抽查的这五天中每天乘车人数是这个问题的( )
A.总体 B.个体 C.样本 D.以上都不对
6.下列调查中,适宜采用全面调查(普查)方式的是( )
A.对一批圆珠笔使用寿命的调查
B.对全国九年级学生身高现状的调查
C.对某品牌烟花爆竹燃放安全的调查
D.对一枚用于发射卫星的运载火箭各零部件的检查
7.为了解中学300名男生的身高情况,随机抽取若干名男生进行身高测量,将所得数据整理后,画出频数分布直方图(如图).估计该校男生的身高在169.5cm~174.5cm之间的人数有( )
A.12 B.48 C.72 D.96
8.某校关注学生的用眼健康,从九年级500名学生中随机抽取了30名学生进行视力检查,发现有12名学生近视眼,据此估计这500名学生中,近视的学生人数约是( )
A.150 B.200 C.350 D.400
9.如图是七年级(1)班参加课外兴趣小组人数的扇形统计图,则表示唱歌兴趣小组人数的扇形的圆心角度数是( )
A.36° B.72° C.108° D.180°
10.如图是杭州市区人口的统计图.则根据统计图得出的下列判断,正确的是( )
A.其中有3个区的人口数都低于40万
B.只有1个区的人口数超过百万
C.上城区与下城区的人口数之和超过江干区的人口数
D.杭州市区的人口数已超过600万
二.填空题(共10小题)
11.某校为了丰富学生的课外体育活动,欲增购一批体育器材,为此该校对一部分学生进行了一次题为“你喜欢的体育活动”的问卷调查(每人限选一项)
根据收集到的数据,绘制成如图的统计图(不完整):
根据图中提供的信息得出“跳绳”部分学生共有 _________ 人.
12.某班主任把本班学生上学方式的调查结果绘制成如图所示的不完整的统计图,已知乘公交车上学的学生有20人,骑自行车上学的学生有26人,则乘公交车上学的学生人数在扇形统计图中对应的扇形所占的圆心角的度数为 _________ .
13.某学校为了了解学生课间体育活动情况,随机抽取本校100名学生进行调查.整理收集到的数据,绘制成如图所示的统计图.若该校共有1200名学生,则估计该校喜欢“踢毽子”的学生有 _________ 人.
14.某校九年级二班的学生在植树节开展“植树造林,绿化城市”的活动,本次活动结束后,该班植树情况的部分统计图如下所示,那么该班的总人数是 _________ 人.
15.在市团委发起的“暖冬行动”中,某班50名同学响应号召,纷纷捐出零花钱.若不同捐款金额的捐款人数百分比统计结果如图所示,则该班同学平均每人捐款 _________ 元.
16.某校为鼓励学生课外阅读,制定了“阅读奖励方案”.方案公布后,随机征求了100名学生的意见,并对持“赞成”、“反对”、“弃权”三种意见的人数进行统计,绘制成如图所示的扇形统计图.若该校有1000名学生,则赞成该方案的学生约有 _________ 人.
17.某初中学校的男生、女生以及教师人数的扇形统计图如图所示,若该校男生、女生以及教师的总人数为1200人,则根据图中信息,可知该校教师共有 _________ 人.
18.小窦将本班学生上学方式的调查结果绘制成如图所示的统计图,若步行上学的学生有27人,则骑车上学的学生有 _________ 人.
19.生物工作者为了估计一片山林中雀鸟的数量,设计了如下方案:先捕捉100只雀鸟,给它们做上标记后放回山林;一段时间后,再从中随机捕捉500只,其中有标记的雀鸟有5只.请你帮助工作人员估计这片山林中雀鸟的数量约为 _________ 只.
20.某班总人数为50人,根据全班学生的课外活动情况绘制的统计图如右图,长跑的人数占30%,跳高的人数占50%,那么参加其他活动的人数为 _________ 人.
三.解答题(共9小题)
21.扬州市中小学全面开展“体艺2+1”活动,某校根据学校实际,决定开设A:篮球,B:乒乓球,C:声乐,D:健美操等四中活动项目,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制了两幅不完整的统计图.请回答下列问题:
(1)这次被调查的学生共有 _________ 人.
(2)请你将统计图1补充完整.
(3)统计图2中D项目对应的扇形的圆心角是 _________ 度.
(4)已知该校学生2400人,请根据调查结果估计该校最喜欢乒乓球的学生人数.
22.第三十届夏季奥林匹克运动会将于2012年7月27日至8月12日在英国伦敦举行,目前正在进行火炬传递活动.某校学生会为了确定近期宣传专刊的主题,想知道学生对伦敦奥运会火炬传递路线的了解程度,决定随机抽取部分学生进行一次问卷调查,并根据收集到的信息进行了统计,绘制了如图两幅上不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有 _________ 名;
(2)请补全折线统计图,并求出扇形统计图中“基本了解”部分所对应扇形的圆心角的大小;
(3)若该校共有1200名学生,请根据上述调查结果估计该校学生中对伦敦奥运火炬传递路线达到了“了解”和“基本了解”程度的总人数.
23.某市园林处去年植树节在滨海路两侧栽了A,B,C三个品种的树苗.栽种的A,B,C三个品种树苗数量的扇形统计图如图(1),其中B种树苗数量对应的扇形圆心角为120°.今年植树节前管理员调查了这三个品种树苗的成活率情况,准备今年从三个品种中选成活率最高的品种再进行栽种.经调查得知:A品种的成活率为85%,三个品种的总成活率为89%,但三个品种树苗成活数量统计图尚不完整,如图(2).
请你根据以上信息帮管理员解决下列问题:
(1)三个品种树苗去年共栽多少棵?
(2)补全条形统计图,并通过计算,说明今年应栽哪个品种的树苗.
24. 2011年徐州市全年实现地区生产总值3551.65亿元,按可比价格计算,比上年增长13.5%,经济平稳较快增长.其中,第一产业、第二产业、第三产业增加值与增长率情况如图所示:
根据图中信息,写成下列填空:
(1)第三产业的增加值为 _________ 亿元:
(2)第三产业的增长率是第一产业增长率的 _________ 倍(精确到0.1);
(3)三个产业中第 _________ 产业的增长最快.
25.为了推动课堂教学改革,打造高效课堂,配合我市“两型课堂”的课题研究,莲城中学对八年级部分学生就一期来“分组合作学习”方式的支持程度进行调查,统计情况如图.试根据图中提供的信息,回答下列问题:
(1)求本次被调查的八年级学生的人数,并补全条形统计图;
(2)若该校八年级学生共有180人,请你估计该校八年级有多少名学生支持“分组合作学习”方式(含“非常喜欢”和“喜欢”两种情况的学生)?
26.某市青少年宫准备在七月一日组织市区部分学校的中小学生到本市A,B,C,D,E五个红色旅游景区“一日游”,每名学生只能在五个景区中任选一个.为估算到各景区旅游的人数,青少年宫随机抽取这些学校的部分学生,进行了“五个红色景区,你最想去哪里”的问卷调查,在统计了所有的调查问卷后将结果绘制成如图所示的统计图.
(1)求参加问卷调查的学生数,并将条形统计图补充完整;
(2)若参加“一日游”的学生为1000人,请估计到C景区旅游的人数.
27.某市为提高学生参与体育活动的积极性,2011年9月围绕“你最喜欢的体育运动项目(只写一项)”这一问题,对初一新生进行随机抽样调查,下图是根据调查结果绘制成的统计图(不完整).
请你根据图中提供的信息解答下列问题:
(1)本次抽样调查的样本容量是多少?
(2)根据条形统计图中的数据,求扇形统计图中“最喜欢足球运动”的学生数所对应扇形的圆心角度数.
(3)请将条形统计图补充完整.
(4)若该市2011年约有初一新生21000人,请你估计全市本届学生中“最喜欢足球运动”的学生约有多少人.
28.某校组织学生书法比赛,对参赛作品按A、B、C、D四个等级进行了评定.现随机抽取部分学生书法作品的评定结果进行分析,并绘制扇形统计图和条形统计图如下:
根据上述信息完成下列问题:
(1)求这次抽取的样本的容量;
(2)请在图②中把条形统计图补充完整;
(3)已知该校这次活动共收到参赛作品750份,请你估计参赛作品达到B级以上(即A级和B级)有多少份?
29.某地为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好地决策,自来水公司随机抽取部分用户的用适量数据,并绘制了如下不完整统计图(每组数据包括右端点但不包括左端点),请你根据统计图解决下列问题:
(1)此次调查抽取了多少用户的用水量数据?
(2)补全频数分布直方图,求扇形统计图中“25吨~30吨”部分的圆心角度数;
(3)如果自来水公司将基本用水量定为每户25吨,那么该地20万用户中约有多少用户的用水全部享受基本价格?
参考答案与试题解析
一.选择题(共10小题)
1.解答:
解:由表知36~42岁及50~56岁的职员人数共有,
200﹣6﹣40﹣42﹣2=110人,
所以,a%+b%=×100%=55%,
所以a+b=55.
故选C.
2.解答:
解:A.日光灯管厂要检测一批灯管的使用寿命,应采用抽样调查方式,故此选项错误;
B.了解衢州市每天的流动人口数,采用抽查方式;故此选项正确;
C.了解衢州市居民日平均用水量,应采用抽样调查方式;故此选项错误;
D.旅客上飞机前的安检,应采用全面调查方式;故此选项错误.
故选:B.
3.解答:
解:了解攀枝花市2012年中考数学学科各分数段成绩分布情况,从中抽取150名考生的中考数学成绩进行统计分析.
样本是,被抽取的150名考生的中考数学成绩,
故选C.
4.解答:
解:①调查一批灯泡的使用寿命,适合抽样调查;
②调查全班同学的身高,适合全面调查;
③调查市场上某种食品的色素含量是否符合国家标准,适合抽样调查;
④企业招聘,对应聘人员进行面试,适合全面调查;
故选B.
5.解答:
解:∵抽查的是“五一”期间每天乘车人数,
∴“五一”期间每天乘车人数是个体.
故选B.
6.解答:
解:A、对一批圆珠笔使用寿命的调查,由于具有破坏性,应当使用抽样调查,故本选项错误;
B、对全国九年级学生身高现状的调查,人数太多,不便于测量,应当采用抽样调查,故本选项错误;
C、对某品牌烟花爆竹燃放安全的调查,由于具有破坏性,应当使用抽样调查,故本选项错误;
D、对一枚用于发射卫星的运载火箭各零部件的检查,只有做到全面调查才能做到准确无误,故必须全面调查,故此选项正确.
故选:D.
7.解答:
解:根据图形,身高在169.5cm~174.5cm之间的人数的百分比为:
×100%=24%,
所以,该校男生的身高在169.5cm~174.5cm之间的人数有300×24%=72(人).
故选C.
8.解答:
解:500×=200人,
即近视的学生人数约200人.
故选B.
9.解答:
解:唱歌所占百分数为:1﹣50%﹣30%=20%,
唱歌兴趣小组人数的扇形的圆心角度数为:360°×20%=72°.
故选B.
10.解答:
解:A、只有上城区人口数都低于40万,故此选项错误;
B、萧山区、余杭区两个区的人口超过100万,故此选项错误;
C、上城区与下城区的人口数之和低于江干区的人口数,故此选项错误;
D、杭州市区的人口数已超过600万,故此选项正确;
故选:D.
二.填空题(共10小题)
11.某校为了丰富学生的课外体育活动,欲增购一批体育器材,为此该校对一部分学生进行了一次题为“你喜欢的体育活动”的问卷调查(每人限选一项)
根据收集到的数据,绘制成如图的统计图(不完整):
根据图中提供的信息得出“跳绳”部分学生共有 50 人.
解答:
解:∵从条形统计图知喜欢球类的有80人,占40%
∴总人数为80÷40%=200人
∴喜欢跳绳的有200﹣80﹣30﹣40=50人,
故答案为50.
12.某班主任把本班学生上学方式的调查结果绘制成如图所示的不完整的统计图,已知乘公交车上学的学生有20人,骑自行车上学的学生有26人,则乘公交车上学的学生人数在扇形统计图中对应的扇形所占的圆心角的度数为 144° .
解答:
解:根据题意得:
总人数是:26÷52%=50人,
所以乘车部分所对应的圆心角的度数为360×=144°;
故答案为:144°.
13.某学校为了了解学生课间体育活动情况,随机抽取本校100名学生进行调查.整理收集到的数据,绘制成如图所示的统计图.若该校共有1200名学生,则估计该校喜欢“踢毽子”的学生有 300 人.
解答:
解:∵随机抽取本校的100名学生中喜欢“踢毽子”的学生有:100﹣40﹣20﹣15=25(人),
∴喜欢“踢毽子”的频率为:25÷100=0.25,
∴该校喜欢“踢毽子”的学生有:1200×0.25=300(人).
故答案为:300.
14.某校九年级二班的学生在植树节开展“植树造林,绿化城市”的活动,本次活动结束后,该班植树情况的部分统计图如下所示,那么该班的总人数是 40 人.
解答:
解:∵植树4株的人数为5人,占总人数的12.5%,
∴该班的总人数=5÷12.5%=40(人).
故答案为40.
15.在资阳市团委发起的“暖冬行动”中,某班50名同学响应号召,纷纷捐出零花钱.若不同捐款金额的捐款人数百分比统计结果如图所示,则该班同学平均每人捐款 14 元.
解答:
解:该班同学平均每人捐款:10×30%+20×20%+50×10%+5×40%=14元.
故答案为14.
16.某校为鼓励学生课外阅读,制定了“阅读奖励方案”.方案公布后,随机征求了100名学生的意见,并对持“赞成”、“反对”、“弃权”三种意见的人数进行统计,绘制成如图所示的扇形统计图.若该校有1000名学生,则赞成该方案的学生约有 700 人.
解答:
解:由扇形统计图可知赞成的百分比为:1﹣20%﹣10%=70%
∴1000名学生中赞成该方案的学生约有1000×70%=700人.
故答案为:700.
17.某初中学校的男生、女生以及教师人数的扇形统计图如图所示,若该校男生、女生以及教师的总人数为1200人,则根据图中信息,可知该校教师共有 108 人.
解答:
解:教师所占的百分比是:1﹣46%﹣45%=9%,
则教师的人数是:1200×9%=108.
故答案是:108.
18.小窦将本班学生上学方式的调查结果绘制成如图所示的统计图,若步行上学的学生有27人,则骑车上学的学生有 9 人.
解答:
解:由图可知步行上学的学生占本班学生上学方式的60%,又知步行上学的学生有27人,
∴本班学生总数=27÷60%=45人,
由图可知骑车的占20%,
∴骑车上学的学生=45×20%=9人.
故答案为9.
19.生物工作者为了估计一片山林中雀鸟的数量,设计了如下方案:先捕捉100只雀鸟,给它们做上标记后放回山林;一段时间后,再从中随机捕捉500只,其中有标记的雀鸟有5只.请你帮助工作人员估计这片山林中雀鸟的数量约为 10000 只.
解答:
解:100=10000只.
故答案为:10000. 20.某班总人数为50人,根据全班学生的课外活动情况绘制的统计图如右图,长跑的人数占30%,跳高的人数占50%,那么参加其他活动的人数为 10 人.
解答:
解:由扇形图知,参加其他活动的人数占全班总人数的百分比为:1﹣30%﹣50%=20%,
又知某班总人数为50人,
∴参加其他活动的人数为 50×20%=10人,
三.解答题(共9小题)
21.扬州市中小学全面开展“体艺2+1”活动,某校根据学校实际,决定开设A:篮球,B:乒乓球,C:声乐,D:健美操等四中活动项目,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制了两幅不完整的统计图.请回答下列问题:
(1)这次被调查的学生共有 200 人.
(2)请你将统计图1补充完整.
(3)统计图2中D项目对应的扇形的圆心角是 72 度.
(4)已知该校学生2400人,请根据调查结果估计该校最喜欢乒乓球的学生人数.
解答:
解:(1)根据喜欢篮球的人数为20人,所占百分比为10%,
故这次被调查的学生共有:20÷10%=200;
故答案为:200;
(2)根据喜欢C音乐的人数=200﹣20﹣80﹣40=60,
故C对应60人,如图所示:
(3)根据喜欢D:健美操的人数为:40人,
则统计图2中D项目对应的扇形的圆心角是:40÷200×360°=72°;
故答案为:72;
(4)根据样本中最喜欢乒乓球的学生人数为80人,
故该校学生2400人中最喜欢乒乓球的学生人数为:×2400=960人.
答:该校最喜欢乒乓球的学生人数大约为960人.
22.第三十届夏季奥林匹克运动会将于2012年7月27日至8月12日在英国伦敦举行,目前正在进行火炬传递活动.某校学生会为了确定近期宣传专刊的主题,想知道学生对伦敦奥运会火炬传递路线的了解程度,决定随机抽取部分学生进行一次问卷调查,并根据收集到的信息进行了统计,绘制了如图两幅上不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有 60 名;
(2)请补全折线统计图,并求出扇形统计图中“基本了解”部分所对应扇形的圆心角的大小;
(3)若该校共有1200名学生,请根据上述调查结果估计该校学生中对伦敦奥运火炬传递路线达到了“了解”和“基本了解”程度的总人数.
解答:
解:(1)根据题意得:30÷50%=60(名)
答:接受问卷调查的学生共有 60名;
(2)如图:60﹣10﹣15﹣30=5(名);
“基本了解”部分所对应扇形的圆心角是:360°×=90°;
(3)该校学生中对伦敦奥运火炬传递路线达到了“了解”和“基本了解”程度的总人数是:
1200×=400(名).
故答案为:60.
23.某市园林处去年植树节在滨海路两侧栽了A,B,C三个品种的树苗.栽种的A,B,C三个品种树苗数量的扇形统计图如图(1),其中B种树苗数量对应的扇形圆心角为120°.今年植树节前管理员调查了这三个品种树苗的成活率情况,准备今年从三个品种中选成活率最高的品种再进行栽种.经调查得知:A品种的成活率为85%,三个品种的总成活率为89%,但三个品种树苗成活数量统计图尚不完整,如图(2).
请你根据以上信息帮管理员解决下列问题:
(1)三个品种树苗去年共栽多少棵?
(2)补全条形统计图,并通过计算,说明今年应栽哪个品种的树苗.
解答:
解:(1)A品种树苗棵数为1020÷85%=1200(棵),
所以,三个品种树苗共栽棵数为1200÷40%=3000(棵);
(2)B品种树苗成活棵数为
3000×89%﹣1020﹣720=930(棵),
补全条形统计图,如图,…(7分)?
B品种树苗成活率为×100%=93%;
C品种树苗成活率为×100%=×100%=90%.
所以,B品种成活率最高,今年应栽B品种树苗.
24. 2011年徐州市全年实现地区生产总值3551.65亿元,按可比价格计算,比上年增长13.5%,经济平稳较快增长.其中,第一产业、第二产业、第三产业增加值与增长率情况如图所示:
根据图中信息,写成下列填空:
(1)第三产业的增加值为 1440.06 亿元:
(2)第三产业的增长率是第一产业增长率的 3.2 倍(精确到0.1);
(3)三个产业中第 二 产业的增长最快.
解答:
解:(1)由左图可知,第三产业的增加值为1440.06亿元,
故答案为:1440.06;
(2)由右图可知,14.50%÷4.50%≈3.2,
故答案为:3.2;
(3)由右图可知,三个产业的增长率依次为:4.50%,14.60%,14.50%,
由此可知,三个产业中第二产业的增长最快,
故答案为:二.
25.为了推动课堂教学改革,打造高效课堂,配合我市“两型课堂”的课题研究,莲城中学对八年级部分学生就一期来“分组合作学习”方式的支持程度进行调查,统计情况如图.试根据图中提供的信息,回答下列问题:
(1)求本次被调查的八年级学生的人数,并补全条形统计图;
(2)若该校八年级学生共有180人,请你估计该校八年级有多少名学生支持“分组合作学习”方式(含“非常喜欢”和“喜欢”两种情况的学生)?
解答:
解:(1)∵喜欢“分组合作学习”方式的圆心角度数为120°,频数为18,
∴喜欢“分组合作学习”方式的总人数为:18÷=54人,
故非常喜欢“分组合作学习”方式的人数为:54﹣18﹣6=30人,如图所示补全条形图即可;
(2)∵“非常喜欢”和“喜欢”两种情况在扇形统计图中所占圆心角为:120°+200°=320°,
∴支持“分组合作学习”方式所占百分比为:×100%,
∴该校八年级学生共有180人,有180×=160名学生支持“分组合作学习”方式.
26.某市青少年宫准备在七月一日组织市区部分学校的中小学生到本市A,B,C,D,E五个红色旅游景区“一日游”,每名学生只能在五个景区中任选一个.为估算到各景区旅游的人数,青少年宫随机抽取这些学校的部分学生,进行了“五个红色景区,你最想去哪里”的问卷调查,在统计了所有的调查问卷后将结果绘制成如图所示的统计图.
(1)求参加问卷调查的学生数,并将条形统计图补充完整;
(2)若参加“一日游”的学生为1000人,请估计到C景区旅游的人数.
解答:
解:(1)50÷25%=200(人),
到B景区旅游的人数是:
200﹣20﹣70﹣10﹣50=50(人),
(2)70÷200=35%,
1000×35%=350(人),
答:估计到C景区旅游的有350人.
27.某市为提高学生参与体育活动的积极性,2011年9月围绕“你最喜欢的体育运动项目(只写一项)”这一问题,对初一新生进行随机抽样调查,下图是根据调查结果绘制成的统计图(不完整).
请你根据图中提供的信息解答下列问题:
(1)本次抽样调查的样本容量是多少?
(2)根据条形统计图中的数据,求扇形统计图中“最喜欢足球运动”的学生数所对应扇形的圆心角度数.
(3)请将条形统计图补充完整.
(4)若该市2011年约有初一新生21000人,请你估计全市本届学生中“最喜欢足球运动”的学生约有多少人.
解答:
解:(1)100÷20%=500,
∴本次抽样调查的样本容量是500;
(2)∵360°×=43.2°,
∴扇形统计图中“最喜欢足球运动”的学生数所对应的扇形圆心角度数为43.2°;
(3)如图:
(4)21000×=2520(人)
全市本届学生中“最喜欢足球运动”的学生约有2520人;
28.某校组织学生书法比赛,对参赛作品按A、B、C、D四个等级进行了评定.现随机抽取部分学生书法作品的评定结果进行分析,并绘制扇形统计图和条形统计图如下:
根据上述信息完成下列问题:
(1)求这次抽取的样本的容量;
(2)请在图②中把条形统计图补充完整;
(3)已知该校这次活动共收到参赛作品750份,请你估计参赛作品达到B级以上(即A级和B级)有多少份?
解答:
解:(1)∵A级人数为24人,在扇形图中所占比例为20%,
∴这次抽取的样本的容量为:24÷20%=120;
(2)根据C级在扇形图中所占比例为30%,
得出C级人数为:120×30%=36人,
∴D级人数为:120﹣36﹣24﹣48=12人,
如图所示:
(3)∵A级和B级作品在样本中所占比例为:(24+48)÷120×100%=60%,
∴该校这次活动共收到参赛作品750份,参赛作品达到B级以上有750×60%=450份.
29.某地为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好地决策,自来水公司随机抽取部分用户的用适量数据,并绘制了如下不完整统计图(每组数据包括右端点但不包括左端点),请你根据统计图解决下列问题:
(1)此次调查抽取了多少用户的用水量数据?
(2)补全频数分布直方图,求扇形统计图中“25吨~30吨”部分的圆心角度数;
(3)如果自来水公司将基本用水量定为每户25吨,那么该地20万用户中约有多少用户的用水全部享受基本价格?
解答:
解:(1)10÷10%=100(户);
(2)100﹣10﹣36﹣25﹣9=100﹣80=20户,画直方图如图,
(画图正确没标记数字同样给分,算出“15﹣﹣20吨”部分的用户数是20但没画图给1分)
×360°=90°;
(3)×20=13.2(万户).
答:该地20万用户中约有13.2万户居民的用水全部享受基本价格.
