数学北师大版(2019)必修第二册 6.3.1空间图形基本位置关系的认识6.3.2刻画空间点、线、 课件(共35张PPT)
文档属性
| 名称 | 数学北师大版(2019)必修第二册 6.3.1空间图形基本位置关系的认识6.3.2刻画空间点、线、 课件(共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-25 00:00:00 | ||
图片预览







文档简介
(共35张PPT)
6.3.1 空间图形基本位置关系的认识
6.3.2 刻画空间点、线、面位置关系的公理(一)
课标阐释
1.通过长方体这一常见的几何体,体会点、直线、平面之间的位置关系.(几何直观)
2.会用数学符号表示点、线、面的位置关系.(数学抽象)
3.掌握平面的基本性质(3个基本事实和3个推论),并能应用其解决点、线、面位置关系的判断和共点、共线、共面等问题的证明.(逻辑推理)
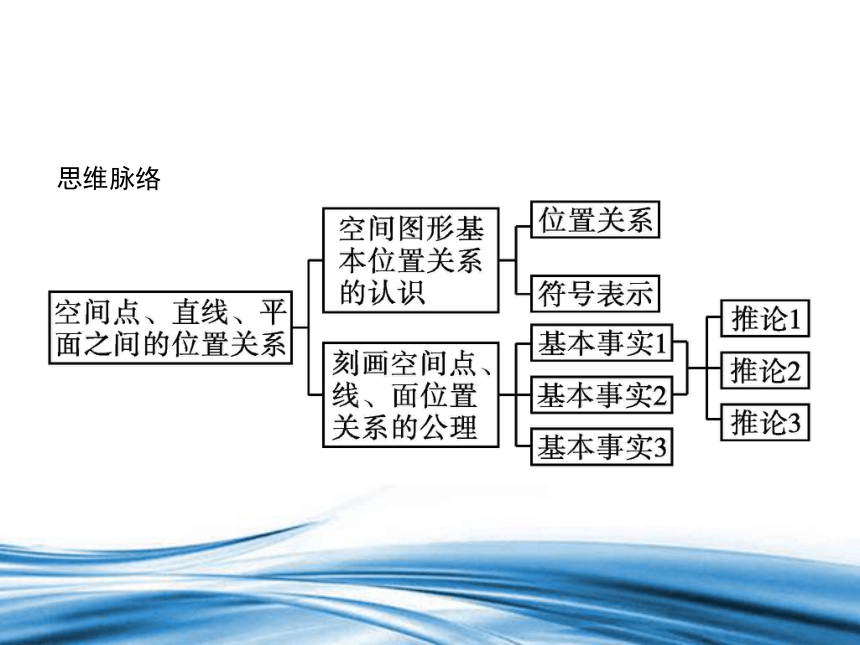
思维脉络
激趣诱思
知识点拨
联合国总部广场万国宫大门对面矗立着一把巨大的三条腿的椅子.这把椅子是瑞士日内瓦艺术家丹尼尔·伯塞特的雕塑作品,是1997年国际残联为了呼吁人们关注战争中地雷对平民造成的伤害而建立的纪念雕塑,象征
人类因触雷而残缺的肢体,但仍然顽强地、有尊严地站立着.伯塞特在设计时,将椅座的位置向上提升,突出长长的椅腿,同时,将椅背设计成弧线形,使整个椅子有微微上翘的感觉,显示它“伤残的尊严”.现在断腿长椅已经成为日内瓦的标志性建筑了.伯塞特的作品给予了我们精神的洗礼,同时也蕴含着数学中的抽象美,思考一下:(1)若要确定一个平面,两个点可以吗 三个点呢 (2)两个平面能否只有一个交点
激趣诱思
知识点拨
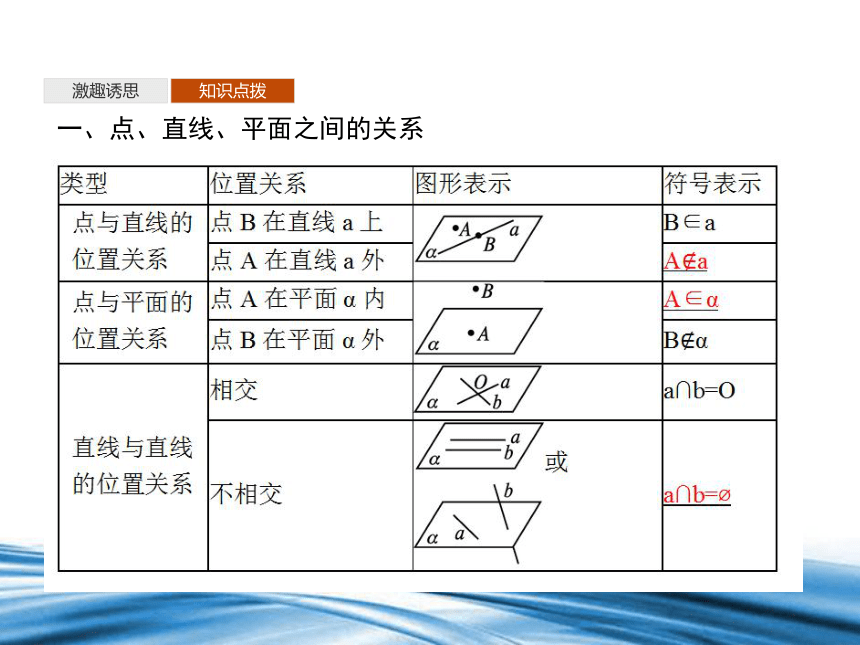
一、点、直线、平面之间的关系
激趣诱思
知识点拨
激趣诱思
知识点拨
激趣诱思
知识点拨
名师点析1.在用符号语言表示点、线、面的关系时,要分清是属于元素和集合的关系,还是集合之间的关系,一般点看成元素,线和面看成点的集合.
2.直线与平面平行和直线与平面相交统称为直线在平面外,即
3.点、线的位置关系用图示表示时可以用平面衬托,线面或面面位置关系的图示表示时要注意线的虚实,被遮挡的要画成虚线或不画.
激趣诱思
知识点拨
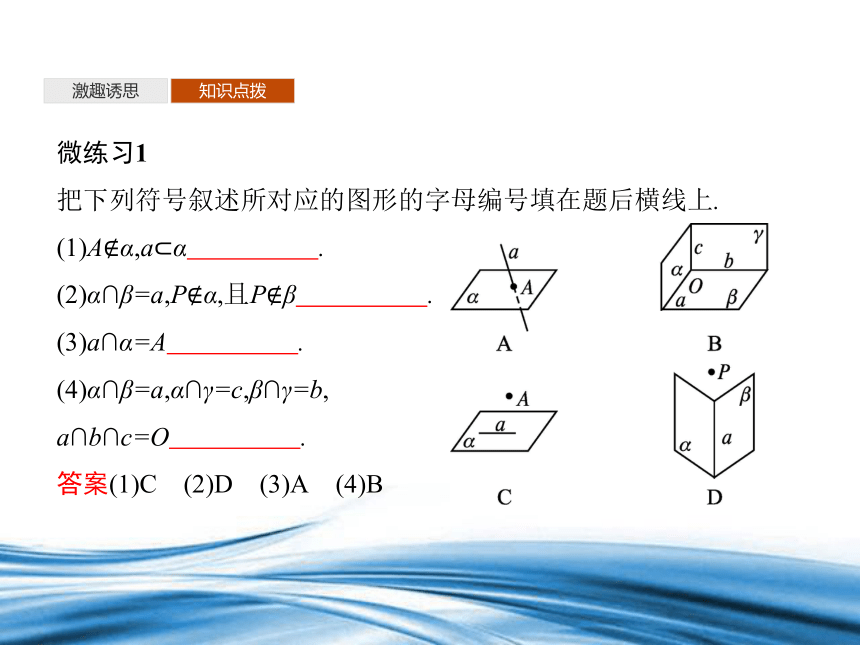
微练习1
把下列符号叙述所对应的图形的字母编号填在题后横线上.
(1)A α,a α .
(2)α∩β=a,P α,且P β .
(3)a∩α=A .
(4)α∩β=a,α∩γ=c,β∩γ=b,
a∩b∩c=O .
答案(1)C (2)D (3)A (4)B
激趣诱思
知识点拨
微练习2
用符号语言表示下列语句,并画出图形.
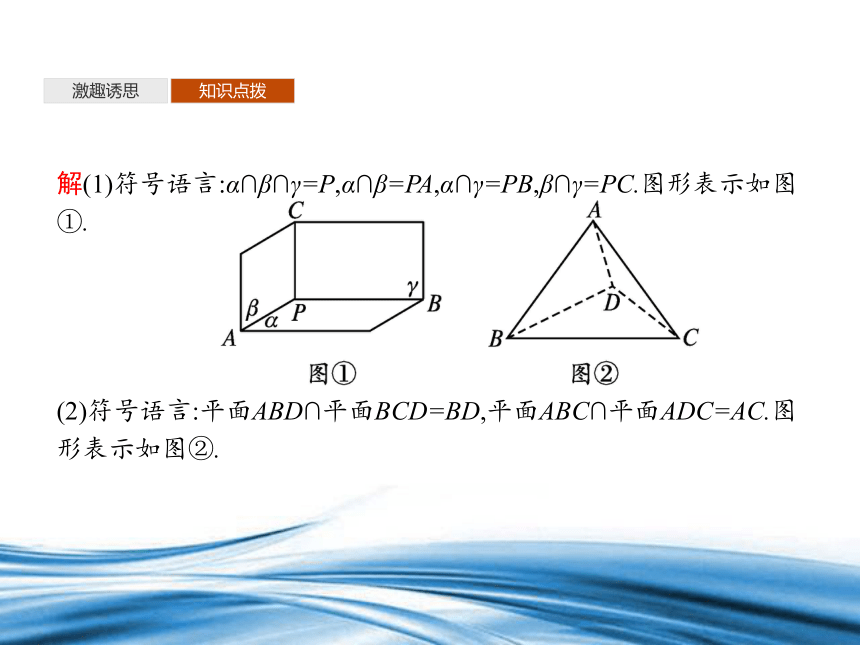
(1)三个平面α,β,γ交于一点P,且平面α与平面β交于PA,平面α与平面γ交于PB,平面β与平面γ交于PC;
(2)平面ABD与平面BCD相交于BD,平面ABC与平面ADC相交于AC.
激趣诱思
知识点拨
解(1)符号语言:α∩β∩γ=P,α∩β=PA,α∩γ=PB,β∩γ=PC.图形表示如图①.
(2)符号语言:平面ABD∩平面BCD=BD,平面ABC∩平面ADC=AC.图形表示如图②.
激趣诱思
知识点拨
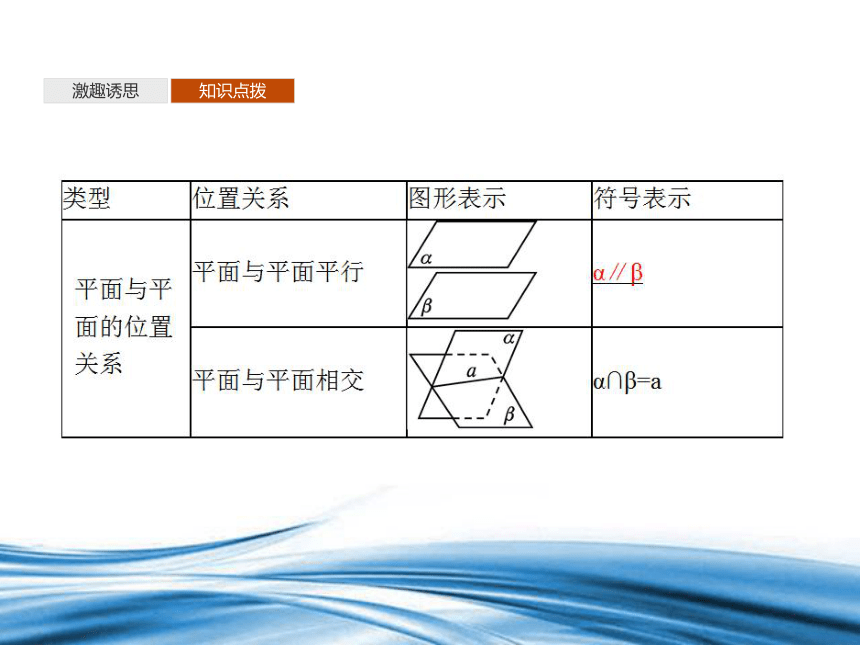
二、平面的基本性质及其推论
1.平面的基本性质
激趣诱思
知识点拨
激趣诱思
知识点拨
2.三个推论
激趣诱思
知识点拨
微思考
两个不重合的平面可能存在有限个公共点吗
提示不能.要么没有公共点,要么有无数个公共点.
微判断
判断(正确的打“√”,错误的打“×”).
(1)两个不重合的平面只能把空间分成四个部分.( )
(2)两个平面α,β有一个公共点A,就说α,β相交于A点,记作α∩β=A.( )
(3)空间不同的三点确定一个平面.( )
(4)两两相交的三条直线最多可以确定三个平面.( )
答案(1)× (2)× (3)× (4)√
探究一
探究二
探究三
探究四
当堂检测
图形语言、文字语言、符号语言的相互转换
例1(1)若点A在直线b上,b在平面β内,则点A,直线b,平面β之间的关系用符号可以记作 .
答案A∈b,b β,A∈β
探究一
探究二
探究三
探究四
当堂检测
(2)用符号表示下列语句,并画出图形.
①点A在平面α内但在平面β外;
②直线a经过平面α内一点A,α外一点B;
③直线a在平面α内,也在平面β内.
解①A∈α,A β.(如图①)
②a∩α=A,B α,B∈a.(如图②)
③α∩β=a.(如图③)
探究一
探究二
探究三
探究四
当堂检测
反思感悟 三种语言转换方法:用文字语言、符号语言表示一个图形时,首先仔细观察图形有几个平面、几条直线及相互之间的位置关系,试着用文字语言表示,再用符号语言表示.
探究一
探究二
探究三
探究四
当堂检测
变式训练1用符号表示下列语句,并画出图形.
(1)平面α与β相交于直线l,直线a与α,β分别相交于点A,B.
(2)点A,B在平面α内,直线a与平面α交于点C,点C不在直线AB上.
解(1)用符号表示α∩β=l,a∩α=A,a∩β=B,如图.
(2)用符号表示A∈α,B∈α,a∩α=C,C AB,如图.
探究一
探究二
探究三
探究四
当堂检测
证明点、线共面
例2证明:两两相交且不过同一点的三条直线共面.
解已知:如图所示,l1∩l2=A,l2∩l3=B,l1∩l3=C.
求证:直线l1,l2,l3在同一平面内.
证明:(方法一)纳入平面法
因为l1∩l2=A,所以l1和l2确定一个平面α.
因为l2∩l3=B,所以B∈l2.又l2 α,所以B∈α.
同理可证C∈α.因为B∈l3,C∈l3,所以l3 α.
所以直线l1,l2,l3在同一平面内.
探究一
探究二
探究三
探究四
当堂检测
(方法二)辅助平面法
因为l1∩l2=A,所以l1,l2确定一个平面α.因为l2∩l3=B,所以l2,l3确定一个平面β.
因为A∈l2,l2 α,所以A∈α.因为A∈l2,l2 β,所以A∈β.
同理可证B∈α,B∈β,C∈α,C∈β.所以不共线的三个点A,B,C既在平面α内,又在平面β内.
所以平面α和β重合,即直线l1,l2,l3在同一平面内.
探究一
探究二
探究三
探究四
当堂检测
反思感悟 证明点、线共面问题的理论依据是基本事实1和基本事实2,常用方法有:
(1)先由部分点、线确定一个面,再证其余的点、线都在这个平面内,即用“纳入平面法”;
(2)先由其中一部分点、线确定一个平面α,其余点、线确定另一个平面β,再证平面α与β重合,即用“辅助平面法”;
(3)假设不共面,结合题设推出矛盾,用“反证法”.
注意:在遇到文字叙述的结论时,一定要先根据题意画出图形,结合图形写出已知与求证,再证明.
探究一
探究二
探究三
探究四
当堂检测
延伸探究把本例中的“不过同一点”删掉呢 这三条直线是否共面
解①不一定共面.
若三条直线两两相交,且过同一个点.
这三条直线在同一个平面内相交,如图.
这三条直线不共面.如图.
②若三条直线两两相交,且不过同一个点,由本例可知,这三条直线共面.
探究一
探究二
探究三
探究四
当堂检测
证明点共线
例3已知△ABC在平面α外,AB∩α=P,AC∩α=R,BC∩α=Q,如图.
求证:P,Q,R三点共线.
探究一
探究二
探究三
探究四
当堂检测
证明(证法一)因为AB∩α=P,所以P∈AB,P∈平面α.
又AB 平面ABC,所以P∈平面ABC.
所以由基本事实3可知点P在平面ABC与平面α的交线上,同理可证Q,R也在平面ABC与平面α的交线上,
所以P,Q,R三点共线.
(证法二)因为AP∩AR=A,
所以直线AP与直线AR确定平面APR.
又AB∩α=P,AC∩α=R,
所以平面APR∩平面α=PR.
因为B∈平面APR,C∈平面APR,
所以BC 平面APR.
因为Q∈BC,所以Q∈平面APR.又Q∈α,
所以Q∈PR,所以P,Q,R三点共线.
探究一
探究二
探究三
探究四
当堂检测
反思感悟 点共线:证明多点共线通常利用基本事实3,即两相交平面交线的唯一性,通过证明点分别在两个平面内,证明点在相交平面的交线上;也可先选择其中两点确定一条直线,再证明其他点也在其上.
探究一
探究二
探究三
探究四
当堂检测
变式训练2如图所示,在正方体ABCD-A1B1C1D1中,设A1C∩平面ABC1D1=E.则B,E,D1三点的关系为 .(填“共线”或“不共线”)
探究一
探究二
探究三
探究四
当堂检测
解析如图所示,连接A1B,BD1,CD1.
因为A1C∩平面ABC1D1=E,
所以E∈A1C,E∈平面ABC1D1.
因为A1C 平面A1BCD1,所以E∈平面A1BCD1.
因为平面A1BCD1∩平面ABC1D1=BD1,所以E∈BD1,
所以B,E,D1三点共线.
答案共线
探究一
探究二
探究三
探究四
当堂检测
证明线共点
例4如图所示,三个平面α,β,γ两两相交于三条直线,即α∩β=c,β∩γ=a,γ∩α=b,若直线a和b不平行,求证:a,b,c三条直线必过同一点.
证明因为α∩γ=b,β∩γ=a,
所以a γ,b γ.
因为直线a和b不平行,所以a,b必相交.
如图所示,设a∩b=P,则P∈a,P∈b.
因为a β,b α,
所以P∈β,P∈α.
又α∩β=c,所以P∈c,即交线c经过点P.
所以a,b,c三条直线必过同一点.
探究一
探究二
探究三
探究四
当堂检测
反思感悟 证明三线共点常用的方法是先说明两条直线共面且相交于一点,再说明这个点在以另一条直线为交线的两个平面内,即该点在另一条直线上,则可得三线共点.
探究一
探究二
探究三
探究四
当堂检测
变式训练3如图所示,在空间四边形ABCD中,E,F分别是AB和CB上的点,G,H分别是CD和AD上的点,且四边形EFGH为梯形,HG∥EF,HG∶EF=1∶3.
求证:EH,BD,FG三条直线相交于同一点.
探究一
探究二
探究三
探究四
当堂检测
证明延长EH,FG,不妨设EH∩FG=O,
因为HG∥EF,HG∶EF=1∶3,且EF≠GH,
所以EH,FG共面,且与FG不平行.
因为O∈EH,EH 平面ABD,所以O∈平面ABD,
因为O∈FG,FG 平面BCD,所以O∈平面BCD.
因为平面ABD∩平面BCD=BD,所以O∈BD,
所以EH,BD,FG三条直线相交于同一点O.
探究一
探究二
探究三
探究四
当堂检测
1.如果点A在直线a上,而直线a在平面α内,点B在平面α内,则可以表示为( )
A.A a,a α,B∈α B.A∈a,a α,B∈α
C.A a,a∈α,B α D.A∈a,a∈α,B∈α
解析点A在直线a上,而直线a在平面α内,点B在平面α内,表示为A∈a,a α,B∈α.
答案B
探究一
探究二
探究三
探究四
当堂检测
2.如图,已知D,E是△ABC的边AC,BC上的点,平面α经过D,E两点,若直线AB与平面α的交点是P,则点P与直线DE的位置关系是 .
解析因为P∈AB,AB 平面ABC,所以P∈平面ABC.又P∈α,平面ABC∩平面α=DE,所以P∈DE.
答案P∈DE
探究一
探究二
探究三
探究四
当堂检测
3.若l1∥l2,l3与l1,l2分别相交于点C,B.求证:l1,l2,l3在同一平面内.
证明因为l1∥l2,所以l1,l2确定一个平面记为α.
因为l1∩l3=C,所以C∈l1.
因为l1 α,所以C∈α.
因为l2∩l3=B,所以B∈l2.因为l2 α,所以B∈α.
因为B∈l3,C∈l3,所以l3 α,即l1,l2,l3在同一平面内.
6.3.1 空间图形基本位置关系的认识
6.3.2 刻画空间点、线、面位置关系的公理(一)
课标阐释
1.通过长方体这一常见的几何体,体会点、直线、平面之间的位置关系.(几何直观)
2.会用数学符号表示点、线、面的位置关系.(数学抽象)
3.掌握平面的基本性质(3个基本事实和3个推论),并能应用其解决点、线、面位置关系的判断和共点、共线、共面等问题的证明.(逻辑推理)
思维脉络
激趣诱思
知识点拨
联合国总部广场万国宫大门对面矗立着一把巨大的三条腿的椅子.这把椅子是瑞士日内瓦艺术家丹尼尔·伯塞特的雕塑作品,是1997年国际残联为了呼吁人们关注战争中地雷对平民造成的伤害而建立的纪念雕塑,象征
人类因触雷而残缺的肢体,但仍然顽强地、有尊严地站立着.伯塞特在设计时,将椅座的位置向上提升,突出长长的椅腿,同时,将椅背设计成弧线形,使整个椅子有微微上翘的感觉,显示它“伤残的尊严”.现在断腿长椅已经成为日内瓦的标志性建筑了.伯塞特的作品给予了我们精神的洗礼,同时也蕴含着数学中的抽象美,思考一下:(1)若要确定一个平面,两个点可以吗 三个点呢 (2)两个平面能否只有一个交点
激趣诱思
知识点拨
一、点、直线、平面之间的关系
激趣诱思
知识点拨
激趣诱思
知识点拨
激趣诱思
知识点拨
名师点析1.在用符号语言表示点、线、面的关系时,要分清是属于元素和集合的关系,还是集合之间的关系,一般点看成元素,线和面看成点的集合.
2.直线与平面平行和直线与平面相交统称为直线在平面外,即
3.点、线的位置关系用图示表示时可以用平面衬托,线面或面面位置关系的图示表示时要注意线的虚实,被遮挡的要画成虚线或不画.
激趣诱思
知识点拨
微练习1
把下列符号叙述所对应的图形的字母编号填在题后横线上.
(1)A α,a α .
(2)α∩β=a,P α,且P β .
(3)a∩α=A .
(4)α∩β=a,α∩γ=c,β∩γ=b,
a∩b∩c=O .
答案(1)C (2)D (3)A (4)B
激趣诱思
知识点拨
微练习2
用符号语言表示下列语句,并画出图形.
(1)三个平面α,β,γ交于一点P,且平面α与平面β交于PA,平面α与平面γ交于PB,平面β与平面γ交于PC;
(2)平面ABD与平面BCD相交于BD,平面ABC与平面ADC相交于AC.
激趣诱思
知识点拨
解(1)符号语言:α∩β∩γ=P,α∩β=PA,α∩γ=PB,β∩γ=PC.图形表示如图①.
(2)符号语言:平面ABD∩平面BCD=BD,平面ABC∩平面ADC=AC.图形表示如图②.
激趣诱思
知识点拨
二、平面的基本性质及其推论
1.平面的基本性质
激趣诱思
知识点拨
激趣诱思
知识点拨
2.三个推论
激趣诱思
知识点拨
微思考
两个不重合的平面可能存在有限个公共点吗
提示不能.要么没有公共点,要么有无数个公共点.
微判断
判断(正确的打“√”,错误的打“×”).
(1)两个不重合的平面只能把空间分成四个部分.( )
(2)两个平面α,β有一个公共点A,就说α,β相交于A点,记作α∩β=A.( )
(3)空间不同的三点确定一个平面.( )
(4)两两相交的三条直线最多可以确定三个平面.( )
答案(1)× (2)× (3)× (4)√
探究一
探究二
探究三
探究四
当堂检测
图形语言、文字语言、符号语言的相互转换
例1(1)若点A在直线b上,b在平面β内,则点A,直线b,平面β之间的关系用符号可以记作 .
答案A∈b,b β,A∈β
探究一
探究二
探究三
探究四
当堂检测
(2)用符号表示下列语句,并画出图形.
①点A在平面α内但在平面β外;
②直线a经过平面α内一点A,α外一点B;
③直线a在平面α内,也在平面β内.
解①A∈α,A β.(如图①)
②a∩α=A,B α,B∈a.(如图②)
③α∩β=a.(如图③)
探究一
探究二
探究三
探究四
当堂检测
反思感悟 三种语言转换方法:用文字语言、符号语言表示一个图形时,首先仔细观察图形有几个平面、几条直线及相互之间的位置关系,试着用文字语言表示,再用符号语言表示.
探究一
探究二
探究三
探究四
当堂检测
变式训练1用符号表示下列语句,并画出图形.
(1)平面α与β相交于直线l,直线a与α,β分别相交于点A,B.
(2)点A,B在平面α内,直线a与平面α交于点C,点C不在直线AB上.
解(1)用符号表示α∩β=l,a∩α=A,a∩β=B,如图.
(2)用符号表示A∈α,B∈α,a∩α=C,C AB,如图.
探究一
探究二
探究三
探究四
当堂检测
证明点、线共面
例2证明:两两相交且不过同一点的三条直线共面.
解已知:如图所示,l1∩l2=A,l2∩l3=B,l1∩l3=C.
求证:直线l1,l2,l3在同一平面内.
证明:(方法一)纳入平面法
因为l1∩l2=A,所以l1和l2确定一个平面α.
因为l2∩l3=B,所以B∈l2.又l2 α,所以B∈α.
同理可证C∈α.因为B∈l3,C∈l3,所以l3 α.
所以直线l1,l2,l3在同一平面内.
探究一
探究二
探究三
探究四
当堂检测
(方法二)辅助平面法
因为l1∩l2=A,所以l1,l2确定一个平面α.因为l2∩l3=B,所以l2,l3确定一个平面β.
因为A∈l2,l2 α,所以A∈α.因为A∈l2,l2 β,所以A∈β.
同理可证B∈α,B∈β,C∈α,C∈β.所以不共线的三个点A,B,C既在平面α内,又在平面β内.
所以平面α和β重合,即直线l1,l2,l3在同一平面内.
探究一
探究二
探究三
探究四
当堂检测
反思感悟 证明点、线共面问题的理论依据是基本事实1和基本事实2,常用方法有:
(1)先由部分点、线确定一个面,再证其余的点、线都在这个平面内,即用“纳入平面法”;
(2)先由其中一部分点、线确定一个平面α,其余点、线确定另一个平面β,再证平面α与β重合,即用“辅助平面法”;
(3)假设不共面,结合题设推出矛盾,用“反证法”.
注意:在遇到文字叙述的结论时,一定要先根据题意画出图形,结合图形写出已知与求证,再证明.
探究一
探究二
探究三
探究四
当堂检测
延伸探究把本例中的“不过同一点”删掉呢 这三条直线是否共面
解①不一定共面.
若三条直线两两相交,且过同一个点.
这三条直线在同一个平面内相交,如图.
这三条直线不共面.如图.
②若三条直线两两相交,且不过同一个点,由本例可知,这三条直线共面.
探究一
探究二
探究三
探究四
当堂检测
证明点共线
例3已知△ABC在平面α外,AB∩α=P,AC∩α=R,BC∩α=Q,如图.
求证:P,Q,R三点共线.
探究一
探究二
探究三
探究四
当堂检测
证明(证法一)因为AB∩α=P,所以P∈AB,P∈平面α.
又AB 平面ABC,所以P∈平面ABC.
所以由基本事实3可知点P在平面ABC与平面α的交线上,同理可证Q,R也在平面ABC与平面α的交线上,
所以P,Q,R三点共线.
(证法二)因为AP∩AR=A,
所以直线AP与直线AR确定平面APR.
又AB∩α=P,AC∩α=R,
所以平面APR∩平面α=PR.
因为B∈平面APR,C∈平面APR,
所以BC 平面APR.
因为Q∈BC,所以Q∈平面APR.又Q∈α,
所以Q∈PR,所以P,Q,R三点共线.
探究一
探究二
探究三
探究四
当堂检测
反思感悟 点共线:证明多点共线通常利用基本事实3,即两相交平面交线的唯一性,通过证明点分别在两个平面内,证明点在相交平面的交线上;也可先选择其中两点确定一条直线,再证明其他点也在其上.
探究一
探究二
探究三
探究四
当堂检测
变式训练2如图所示,在正方体ABCD-A1B1C1D1中,设A1C∩平面ABC1D1=E.则B,E,D1三点的关系为 .(填“共线”或“不共线”)
探究一
探究二
探究三
探究四
当堂检测
解析如图所示,连接A1B,BD1,CD1.
因为A1C∩平面ABC1D1=E,
所以E∈A1C,E∈平面ABC1D1.
因为A1C 平面A1BCD1,所以E∈平面A1BCD1.
因为平面A1BCD1∩平面ABC1D1=BD1,所以E∈BD1,
所以B,E,D1三点共线.
答案共线
探究一
探究二
探究三
探究四
当堂检测
证明线共点
例4如图所示,三个平面α,β,γ两两相交于三条直线,即α∩β=c,β∩γ=a,γ∩α=b,若直线a和b不平行,求证:a,b,c三条直线必过同一点.
证明因为α∩γ=b,β∩γ=a,
所以a γ,b γ.
因为直线a和b不平行,所以a,b必相交.
如图所示,设a∩b=P,则P∈a,P∈b.
因为a β,b α,
所以P∈β,P∈α.
又α∩β=c,所以P∈c,即交线c经过点P.
所以a,b,c三条直线必过同一点.
探究一
探究二
探究三
探究四
当堂检测
反思感悟 证明三线共点常用的方法是先说明两条直线共面且相交于一点,再说明这个点在以另一条直线为交线的两个平面内,即该点在另一条直线上,则可得三线共点.
探究一
探究二
探究三
探究四
当堂检测
变式训练3如图所示,在空间四边形ABCD中,E,F分别是AB和CB上的点,G,H分别是CD和AD上的点,且四边形EFGH为梯形,HG∥EF,HG∶EF=1∶3.
求证:EH,BD,FG三条直线相交于同一点.
探究一
探究二
探究三
探究四
当堂检测
证明延长EH,FG,不妨设EH∩FG=O,
因为HG∥EF,HG∶EF=1∶3,且EF≠GH,
所以EH,FG共面,且与FG不平行.
因为O∈EH,EH 平面ABD,所以O∈平面ABD,
因为O∈FG,FG 平面BCD,所以O∈平面BCD.
因为平面ABD∩平面BCD=BD,所以O∈BD,
所以EH,BD,FG三条直线相交于同一点O.
探究一
探究二
探究三
探究四
当堂检测
1.如果点A在直线a上,而直线a在平面α内,点B在平面α内,则可以表示为( )
A.A a,a α,B∈α B.A∈a,a α,B∈α
C.A a,a∈α,B α D.A∈a,a∈α,B∈α
解析点A在直线a上,而直线a在平面α内,点B在平面α内,表示为A∈a,a α,B∈α.
答案B
探究一
探究二
探究三
探究四
当堂检测
2.如图,已知D,E是△ABC的边AC,BC上的点,平面α经过D,E两点,若直线AB与平面α的交点是P,则点P与直线DE的位置关系是 .
解析因为P∈AB,AB 平面ABC,所以P∈平面ABC.又P∈α,平面ABC∩平面α=DE,所以P∈DE.
答案P∈DE
探究一
探究二
探究三
探究四
当堂检测
3.若l1∥l2,l3与l1,l2分别相交于点C,B.求证:l1,l2,l3在同一平面内.
证明因为l1∥l2,所以l1,l2确定一个平面记为α.
因为l1∩l3=C,所以C∈l1.
因为l1 α,所以C∈α.
因为l2∩l3=B,所以B∈l2.因为l2 α,所以B∈α.
因为B∈l3,C∈l3,所以l3 α,即l1,l2,l3在同一平面内.
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
