青岛版八年级数学下册 第6章 平行四边形单元测试(word版含答案)
文档属性
| 名称 | 青岛版八年级数学下册 第6章 平行四边形单元测试(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 176.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-25 14:24:17 | ||
图片预览

文档简介
第6章 平行四边形
一、选择题(每小题3分,共24分)
1、对角线互相垂直平分的四边形是( )
A、平行四边形 B、矩形 C、菱形 D、梯形
2、平行四边形ABCD的周长32,5AB=3BC,则对角线AC的取值范围为( )
A、63、矩形的面积为120cm2,周长为46cm,则它的对角线长为( )
A、15cm B、16cm C、17cm D、18cm
4、A、B、C、D在同一平面内,从①AB∥CD;②AB=CD;③BC∥AD;④BC=AD;这四个条件中任选两个,能使四边形ABCD成为平行四边形的选法共有( )
A、3种 B、4种 C、5种 D、6种
5、如图,过矩形ABCD的四个顶点作对角线AC、BD的平行线,分别相交于E、F、G、H四点,则四边形EFGH为( )
A、平行四边形 B、矩形 C、菱形 D、正方形
6、在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是某合作学习小组的4位同学拟定的方案,其中正确的是( )
A、测量对角线是否相互平分 B、测量两组对边是否分别相等
C、测量一组对角是否都为直角 D、测量其中三角形是否都为直角
7、如图,在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连接EF.若∠BEC=60°,则∠EFD的度数为( )
A、10° B、15° C、20° D、25°
第7题 第8题
8、如图,□ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3 cm,则AB的长为( )
A、3cm B、6cm C、9cm D、12cm
二、填空题(每小题3分,共9分)
9、如图所示,将两条等宽的纸条重叠在一起,则四边形ABCD是,若AB=8,∠ABC=60°,则AC=,BD=。
第9题 第10题
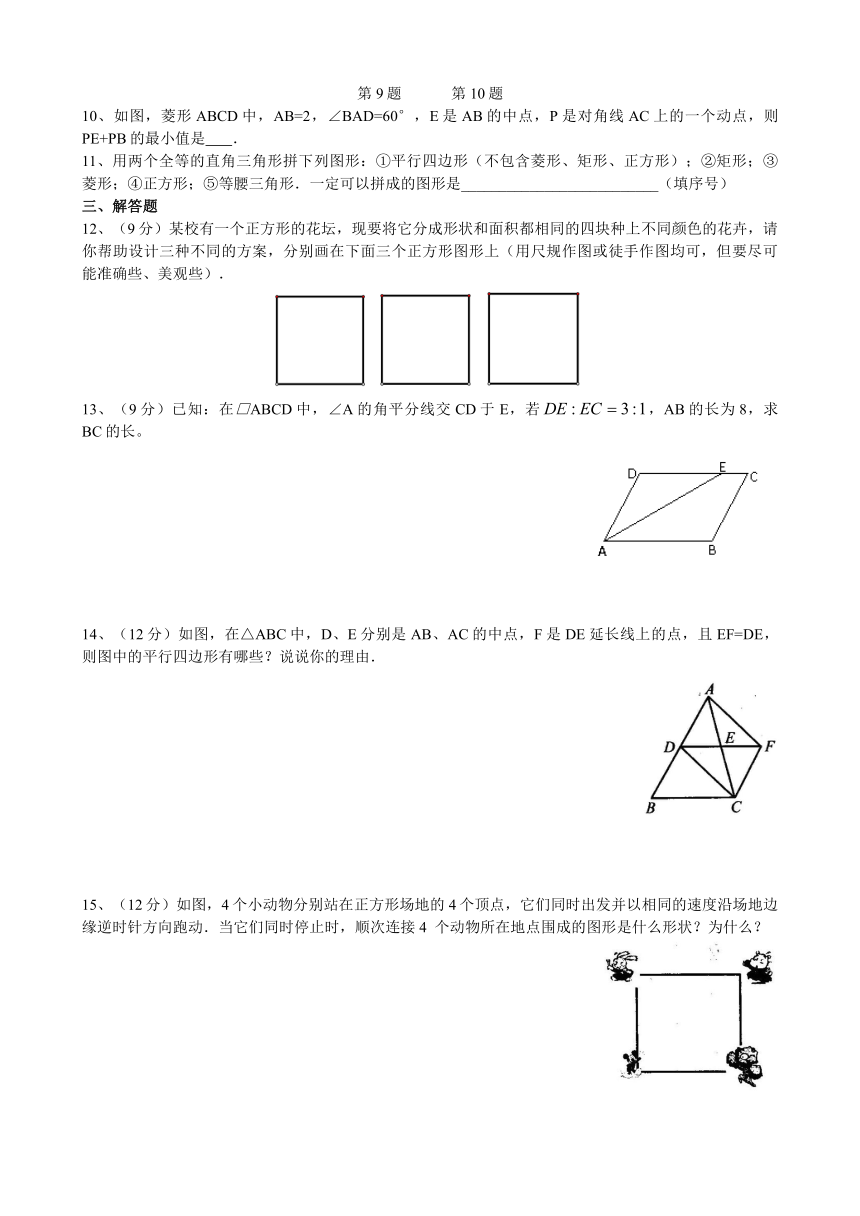
10、如图,菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是 .
11、用两个全等的直角三角形拼下列图形:①平行四边形(不包含菱形、矩形、正方形);②矩形;③菱形;④正方形;⑤等腰三角形.一定可以拼成的图形是__________________________(填序号)
三、解答题
12、(9分)某校有一个正方形的花坛,现要将它分成形状和面积都相同的四块种上不同颜色的花卉,请你帮助设计三种不同的方案,分别画在下面三个正方形图形上(用尺规作图或徒手作图均可,但要尽可能准确些、美观些).
13、(9分)已知:在□ABCD中,∠A的角平分线交CD于E,若,AB的长为8,求BC的长。
14、(12分)如图,在△ABC中,D、E分别是AB、AC的中点,F是DE延长线上的点,且EF=DE,则图中的平行四边形有哪些?说说你的理由.
15、(12分)如图,4个小动物分别站在正方形场地的4个顶点,它们同时出发并以相同的速度沿场地边缘逆时针方向跑动.当它们同时停止时,顺次连接4个动物所在地点围成的图形是什么形状?为什么?
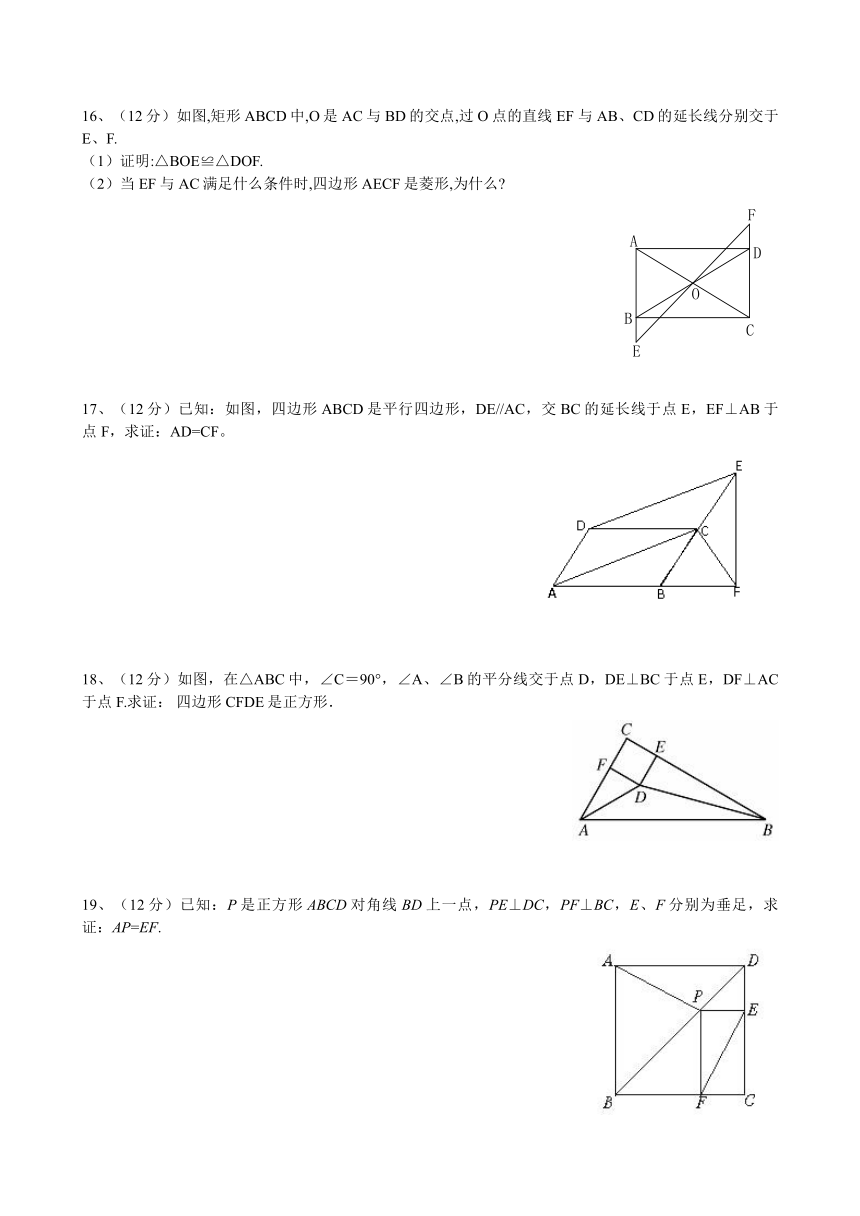
16、(12分)如图,矩形ABCD中,O是AC与BD的交点,过O点的直线EF 与AB、CD的延长线分别交于E、F.
(1)证明:△BOE≌△DOF.
(2)当EF与AC满足什么条件时,四边形AECF是菱形,为什么
17、(12分)已知:如图,四边形ABCD是平行四边形,DE//AC,交BC的延长线于点E,EF⊥AB于点F,求证:AD=CF。
18、(12分)如图,在△ABC中,∠C=90°,∠A、∠B的平分线交于点D,DE⊥BC于点E,DF⊥AC于点F.求证: 四边形CFDE是正方形.
19、(12分)已知:P是正方形ABCD对角线BD上一点,PE⊥DC,PF⊥BC,E、F分别为垂足,求证:AP=EF.
参考答案
1.C 2.D 3.C 4.B 5.C 6.D 7.B 8.B 9、菱形;8; 10、 11、①② ⑤
12、
13、∵ 四边形ABCD是平行四边形,
∴ AD=BC,CD//AB,CD=AB,
∴ ∠DEA=∠EAB,
∵ CD平分∠DAB,∴∠EAB=∠DAE,
∴∠DEA=∠DAE,∴AD=DE=BC.
∵ AB=8,且,∴ DE=BC=6.
14、平行四边形:□BCDF和□ADCF.
∵ 点D、E分别是AB、AC的中点,
∴ DE是△ABC的中位线,∴DE//BC,DE=BC.
∵EF=DE,∴DF=EF+DE=BC.
∴四边形BCDF是平行四边形.
又AE=CE,DE=EF,∴四边形ADCF是平行四边形.
15、矩形 由于速度和时间都相同,所以它们走过的路程相等。
如图, AE=BF=CG=DH.
∵四边形ABCD是正方形
∴AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°
∵AE=BF=CG=DH ,∴EB=FC=GD=HA.
∴△AEH≌△BFE≌△CGF≌△DHG.
∴EH=EF=FG=GH,∴四边形EFGH是菱形.
又∵△AEH≌△BFE,∴∠AEH=∠BFE.
∵∠BEF+∠BFE=90°,∴∠AEH+∠BEF=90°.
∴∠HEF=90°,∴菱形EFGH是正方形.
16、(1)∵四边形ABCD是矩形,∴AB//CD,BO=DO.
∴∠E=∠F,∠EBO=∠FDO,∴△BOE≌△DOF.
(2)当EF⊥AC时,四边形AECF是菱形
∵四边形ABCD是矩形,∴AO=CO.
∵△BOE≌△DOF,∴EO=FO.
∴四边形AECF是平行四边形.
∵EF⊥AC,∴四边形AECF是菱形.
17、∵四边形ABCD是平行四边形,
∴AD=BC,AD//BC.
∵DE//AC, ∴四边形ACED是平行四边形.
∴AD=CE, ∴BC=CE=BE.
∵EF⊥AB,∴∠BFE=90°.
∵CF是Rt△BFE斜边上的中线,
∴CF=BE,∴AD=CF.
18、过点D作DH⊥AB于点H
∵DE⊥BC,DF⊥AC,且∠C=90°,∴∠C=∠CFD=∠CED=90°∴四边形CFDE是矩形.
∵AD是∠CAB的平分线,且DF⊥AC,DH⊥AB
∴DF=DH.同理可得DE=DH.∴DE=DF.
∴四边形CFDE是正方形.
19、连结PC
∵四边形ABCD是正方形,BD为对角线
∴∠BCD=90°,AB=BC,∠ABP=∠CBP.
又∵BP=BP,∴△ABP≌△CBP.∴AP=BP.
∵PE⊥DC,PF⊥BC,∴∠PFC=∠PEC=∠BCD=90°
∴四边形PFCE是矩形,∴PC=FE,∴AP=EF.
一、选择题(每小题3分,共24分)
1、对角线互相垂直平分的四边形是( )
A、平行四边形 B、矩形 C、菱形 D、梯形
2、平行四边形ABCD的周长32,5AB=3BC,则对角线AC的取值范围为( )
A、6
A、15cm B、16cm C、17cm D、18cm
4、A、B、C、D在同一平面内,从①AB∥CD;②AB=CD;③BC∥AD;④BC=AD;这四个条件中任选两个,能使四边形ABCD成为平行四边形的选法共有( )
A、3种 B、4种 C、5种 D、6种
5、如图,过矩形ABCD的四个顶点作对角线AC、BD的平行线,分别相交于E、F、G、H四点,则四边形EFGH为( )
A、平行四边形 B、矩形 C、菱形 D、正方形
6、在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是某合作学习小组的4位同学拟定的方案,其中正确的是( )
A、测量对角线是否相互平分 B、测量两组对边是否分别相等
C、测量一组对角是否都为直角 D、测量其中三角形是否都为直角
7、如图,在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连接EF.若∠BEC=60°,则∠EFD的度数为( )
A、10° B、15° C、20° D、25°
第7题 第8题
8、如图,□ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3 cm,则AB的长为( )
A、3cm B、6cm C、9cm D、12cm
二、填空题(每小题3分,共9分)
9、如图所示,将两条等宽的纸条重叠在一起,则四边形ABCD是,若AB=8,∠ABC=60°,则AC=,BD=。
第9题 第10题
10、如图,菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是 .
11、用两个全等的直角三角形拼下列图形:①平行四边形(不包含菱形、矩形、正方形);②矩形;③菱形;④正方形;⑤等腰三角形.一定可以拼成的图形是__________________________(填序号)
三、解答题
12、(9分)某校有一个正方形的花坛,现要将它分成形状和面积都相同的四块种上不同颜色的花卉,请你帮助设计三种不同的方案,分别画在下面三个正方形图形上(用尺规作图或徒手作图均可,但要尽可能准确些、美观些).
13、(9分)已知:在□ABCD中,∠A的角平分线交CD于E,若,AB的长为8,求BC的长。
14、(12分)如图,在△ABC中,D、E分别是AB、AC的中点,F是DE延长线上的点,且EF=DE,则图中的平行四边形有哪些?说说你的理由.
15、(12分)如图,4个小动物分别站在正方形场地的4个顶点,它们同时出发并以相同的速度沿场地边缘逆时针方向跑动.当它们同时停止时,顺次连接4个动物所在地点围成的图形是什么形状?为什么?
16、(12分)如图,矩形ABCD中,O是AC与BD的交点,过O点的直线EF 与AB、CD的延长线分别交于E、F.
(1)证明:△BOE≌△DOF.
(2)当EF与AC满足什么条件时,四边形AECF是菱形,为什么
17、(12分)已知:如图,四边形ABCD是平行四边形,DE//AC,交BC的延长线于点E,EF⊥AB于点F,求证:AD=CF。
18、(12分)如图,在△ABC中,∠C=90°,∠A、∠B的平分线交于点D,DE⊥BC于点E,DF⊥AC于点F.求证: 四边形CFDE是正方形.
19、(12分)已知:P是正方形ABCD对角线BD上一点,PE⊥DC,PF⊥BC,E、F分别为垂足,求证:AP=EF.
参考答案
1.C 2.D 3.C 4.B 5.C 6.D 7.B 8.B 9、菱形;8; 10、 11、①② ⑤
12、
13、∵ 四边形ABCD是平行四边形,
∴ AD=BC,CD//AB,CD=AB,
∴ ∠DEA=∠EAB,
∵ CD平分∠DAB,∴∠EAB=∠DAE,
∴∠DEA=∠DAE,∴AD=DE=BC.
∵ AB=8,且,∴ DE=BC=6.
14、平行四边形:□BCDF和□ADCF.
∵ 点D、E分别是AB、AC的中点,
∴ DE是△ABC的中位线,∴DE//BC,DE=BC.
∵EF=DE,∴DF=EF+DE=BC.
∴四边形BCDF是平行四边形.
又AE=CE,DE=EF,∴四边形ADCF是平行四边形.
15、矩形 由于速度和时间都相同,所以它们走过的路程相等。
如图, AE=BF=CG=DH.
∵四边形ABCD是正方形
∴AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°
∵AE=BF=CG=DH ,∴EB=FC=GD=HA.
∴△AEH≌△BFE≌△CGF≌△DHG.
∴EH=EF=FG=GH,∴四边形EFGH是菱形.
又∵△AEH≌△BFE,∴∠AEH=∠BFE.
∵∠BEF+∠BFE=90°,∴∠AEH+∠BEF=90°.
∴∠HEF=90°,∴菱形EFGH是正方形.
16、(1)∵四边形ABCD是矩形,∴AB//CD,BO=DO.
∴∠E=∠F,∠EBO=∠FDO,∴△BOE≌△DOF.
(2)当EF⊥AC时,四边形AECF是菱形
∵四边形ABCD是矩形,∴AO=CO.
∵△BOE≌△DOF,∴EO=FO.
∴四边形AECF是平行四边形.
∵EF⊥AC,∴四边形AECF是菱形.
17、∵四边形ABCD是平行四边形,
∴AD=BC,AD//BC.
∵DE//AC, ∴四边形ACED是平行四边形.
∴AD=CE, ∴BC=CE=BE.
∵EF⊥AB,∴∠BFE=90°.
∵CF是Rt△BFE斜边上的中线,
∴CF=BE,∴AD=CF.
18、过点D作DH⊥AB于点H
∵DE⊥BC,DF⊥AC,且∠C=90°,∴∠C=∠CFD=∠CED=90°∴四边形CFDE是矩形.
∵AD是∠CAB的平分线,且DF⊥AC,DH⊥AB
∴DF=DH.同理可得DE=DH.∴DE=DF.
∴四边形CFDE是正方形.
19、连结PC
∵四边形ABCD是正方形,BD为对角线
∴∠BCD=90°,AB=BC,∠ABP=∠CBP.
又∵BP=BP,∴△ABP≌△CBP.∴AP=BP.
∵PE⊥DC,PF⊥BC,∴∠PFC=∠PEC=∠BCD=90°
∴四边形PFCE是矩形,∴PC=FE,∴AP=EF.
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
