23.2中心对称复习练习(附答案解析)
文档属性
| 名称 | 23.2中心对称复习练习(附答案解析) |  | |
| 格式 | zip | ||
| 文件大小 | 37.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-07 23:17:16 | ||
图片预览

文档简介
中心对称
一、知识点: (一)中心对称 把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,则称这两个图形关于这个点对称或中心对称,这个点叫做对称中心,这两个图形中的对应点叫做关于中心的对称点.
(二)中心对称的特征: 1.关于中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分。 2.关于中心对称的两个图形是全等图形。
(三)中心对称图形: 中心对称图形是一种特殊的旋转对称图形.一个图形绕着某一点旋转180°后,如果旋转后的图形能够与原来的图形重合,则这种图形叫做中心对称图形,这个点叫做对称中心.
二、典型例题: (一)基础题型: 1.下列说法中,不正确的是( ) A.轴对称图形的对称轴是对称点连线的垂直平分线 B.中心对称图形的对称中心是对称点连线的中点 C.成轴对称的两个图形中,对应线段相等 D.成中心对称的两个图形中,对应线段平行且相等
解析:选D。成中心对称的两个图形中,对应线段相等,有可能平行,还有可能在同一直线上。
2.在线段、等腰梯形、平行四边形、矩形、菱形、正方形、等边三角形中,既是轴对称图形,又是中心对称图形的图形有( ) A.3个 B.4个 C.5个 D.6个
解析:选B。线段、矩形、菱形、正方形既是轴对称图形,又是中心对称图形;等腰梯形、等边三角形是轴对称图形;平行四边形是中心对称图形。
3.选出下列图形中的中心对称图形( ) ① ② ③ ④ A.①② B.①③ C.②③ D.③④
解析:选B。根据定义,一个图形绕着某一点旋转180°后,如果旋转后的图形能够与原来的图形重合,则这种图形叫做中心对称图形。
4.在等腰三角形、等边三角形、菱形、等腰梯形中是轴对称图形,但不是中心对称图形个数是( ) A. 1个 B. 2个 C. 3个 D. 4个
解析:选C。等腰三角形、等边三角形、等腰梯形是轴对称图形,不是中心对称图形;菱形则既是轴对称图形,又是中心对称图形。
5.下列图形中,不是中心对称图形的是( ) A. 菱形 B. 矩形 C. 正方形 D. 等边三角形 解析:选D。等边三角形是轴对称图形。
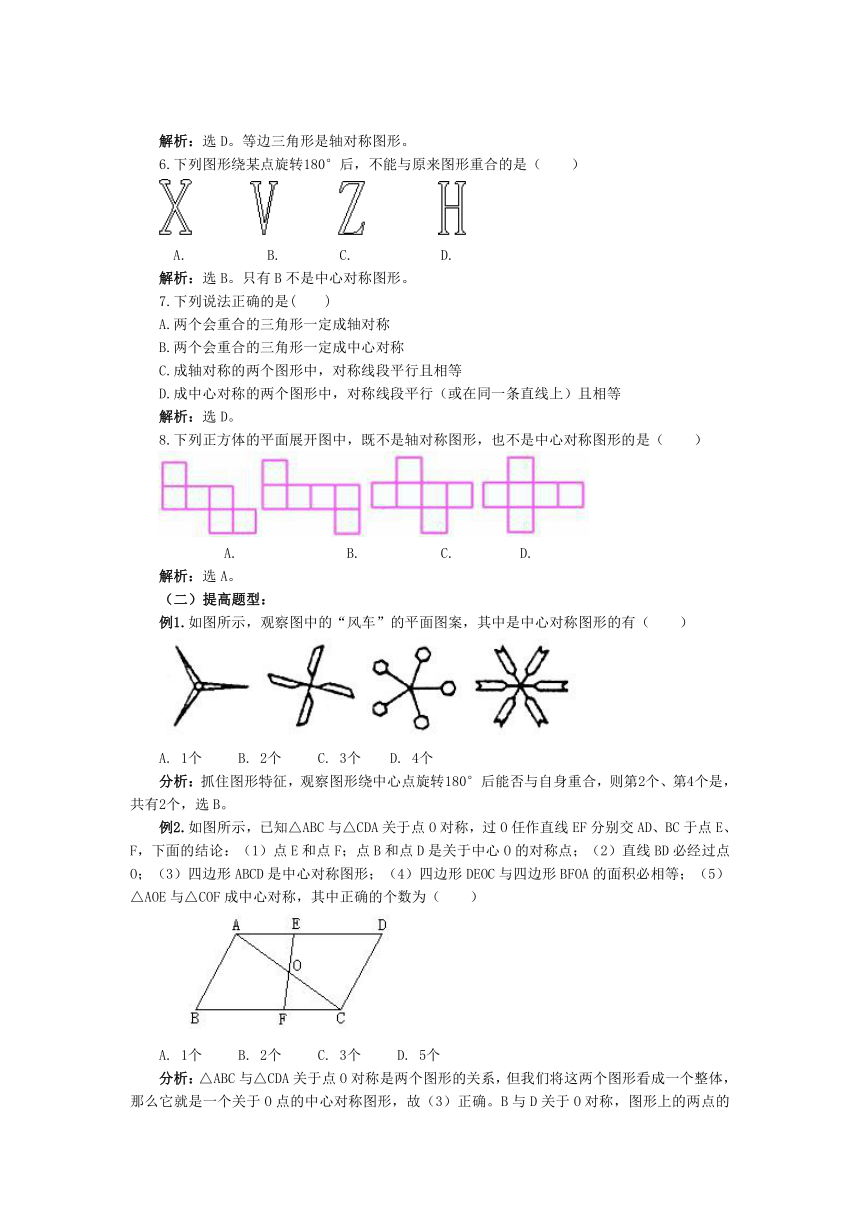
6.下列图形绕某点旋转180°后,不能与原来图形重合的是( ) A. B. C. D.
解析:选B。只有B不是中心对称图形。
7.下列说法正确的是( ) A.两个会重合的三角形一定成轴对称 B.两个会重合的三角形一定成中心对称 C.成轴对称的两个图形中,对称线段平行且相等 D.成中心对称的两个图形中,对称线段平行(或在同一条直线上)且相等
解析:选D。
8.下列正方体的平面展开图中,既不是轴对称图形,也不是中心对称图形的是( ) A. B. C. D.
解析:选A。
(二)提高题型: 例1.如图所示,观察图中的“风车”的平面图案,其中是中心对称图形的有( )
A. 1个 B. 2个 C. 3个 D. 4个
分析:抓住图形特征,观察图形绕中心点旋转180°后能否与自身重合,则第2个、第4个是,共有2个,选B。
例2.如图所示,已知△ABC与△CDA关于点O对称,过O任作直线EF分别交AD、BC于点E、F,下面的结论:(1)点E和点F;点B和点D是关于中心O的对称点;(2)直线BD必经过点O;(3)四边形ABCD是中心对称图形;(4)四边形DEOC与四边形BFOA的面积必相等;(5)△AOE与△COF成中心对称,其中正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 5个
分析:△ABC与△CDA关于点O对称是两个图形的关系,但我们将这两个图形看成一个整体,那么它就是一个关于O点的中心对称图形,故(3)正确。B与D关于O对称,图形上的两点的连线若经过中心,这两点就是对称点,同时对称点的连线必经过对称中心,所以(1)(2)都正确;从中心对称图形的性质得知,四边形DEOC与四边形BFOA是四对对称点所围成的图形,△AOE与△COF也是对称点所围成的图形,所以它们分别成中心对称,故(4)和(5)都正确。选D
例3.某同学学习了几何中的对称后,忽然想起了过去做过一道题:有一组数排成方阵,如图所示,试计算这组数的和。这个同学想,方阵就象正方形,正方形是轴对称图形,也是中心对称图形,能不能利用轴对称和中心对称的思想来解决方阵的计算问题吗?这个同学试了试,竟得到了非常巧妙的方法,你也能试试看吗?
下面将这位同学的想法告诉大家,我们一起来体验一下。
从方阵中的数看出,一条对角线上的数都是5,若把这条对角线当作轴,把正方形翻折一下,对称位置的两数之和都是10,这样方阵中数的和即可求。也可考虑:把方阵绕中心旋转180°,就得到另一方阵,再加到原来的方阵上去,就得到所有的数都是
10的方阵,这一方阵数的和亦可求。
解法一: 解法二:
此题还可引伸成解决其它数学问题。
当在求一组有规律的数的和时,经常会用到对称思想。如: 考虑: 所以
因此,数形结合是学习数学的一种重要思想方法。
例4. 一块方角形钢板(如图所示),如何用一条直线将其分为面积相等的两部分。
解析:首先考虑分形(分成n个规则图形)。 (1)该钢板可看成由上下两个矩形构成(如图所示),矩形是中心对称图形,过对称中心的任一直线把矩形分成全等的两部分,自然平分其面积,而矩形的对称中心是两条对角线的交点,因此,先作出两矩形的对称中心A、B,直线AB即为所求;
(2)该钢板同样可看成左右两矩形构成(如图所示),作出两矩形对称中心C,D,直线CD也符合要求;
(3)将钢板补成一个完整矩形(如图所示),作出大矩形对称中心E和补上一块矩形的对称中心F,直线EF既平分大矩形,又平分补充矩形的面积,于是EF平分原钢板面积。
一、知识点: (一)中心对称 把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,则称这两个图形关于这个点对称或中心对称,这个点叫做对称中心,这两个图形中的对应点叫做关于中心的对称点.
(二)中心对称的特征: 1.关于中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分。 2.关于中心对称的两个图形是全等图形。
(三)中心对称图形: 中心对称图形是一种特殊的旋转对称图形.一个图形绕着某一点旋转180°后,如果旋转后的图形能够与原来的图形重合,则这种图形叫做中心对称图形,这个点叫做对称中心.
二、典型例题: (一)基础题型: 1.下列说法中,不正确的是( ) A.轴对称图形的对称轴是对称点连线的垂直平分线 B.中心对称图形的对称中心是对称点连线的中点 C.成轴对称的两个图形中,对应线段相等 D.成中心对称的两个图形中,对应线段平行且相等
解析:选D。成中心对称的两个图形中,对应线段相等,有可能平行,还有可能在同一直线上。
2.在线段、等腰梯形、平行四边形、矩形、菱形、正方形、等边三角形中,既是轴对称图形,又是中心对称图形的图形有( ) A.3个 B.4个 C.5个 D.6个
解析:选B。线段、矩形、菱形、正方形既是轴对称图形,又是中心对称图形;等腰梯形、等边三角形是轴对称图形;平行四边形是中心对称图形。
3.选出下列图形中的中心对称图形( ) ① ② ③ ④ A.①② B.①③ C.②③ D.③④
解析:选B。根据定义,一个图形绕着某一点旋转180°后,如果旋转后的图形能够与原来的图形重合,则这种图形叫做中心对称图形。
4.在等腰三角形、等边三角形、菱形、等腰梯形中是轴对称图形,但不是中心对称图形个数是( ) A. 1个 B. 2个 C. 3个 D. 4个
解析:选C。等腰三角形、等边三角形、等腰梯形是轴对称图形,不是中心对称图形;菱形则既是轴对称图形,又是中心对称图形。
5.下列图形中,不是中心对称图形的是( ) A. 菱形 B. 矩形 C. 正方形 D. 等边三角形 解析:选D。等边三角形是轴对称图形。
6.下列图形绕某点旋转180°后,不能与原来图形重合的是( ) A. B. C. D.
解析:选B。只有B不是中心对称图形。
7.下列说法正确的是( ) A.两个会重合的三角形一定成轴对称 B.两个会重合的三角形一定成中心对称 C.成轴对称的两个图形中,对称线段平行且相等 D.成中心对称的两个图形中,对称线段平行(或在同一条直线上)且相等
解析:选D。
8.下列正方体的平面展开图中,既不是轴对称图形,也不是中心对称图形的是( ) A. B. C. D.
解析:选A。
(二)提高题型: 例1.如图所示,观察图中的“风车”的平面图案,其中是中心对称图形的有( )
A. 1个 B. 2个 C. 3个 D. 4个
分析:抓住图形特征,观察图形绕中心点旋转180°后能否与自身重合,则第2个、第4个是,共有2个,选B。
例2.如图所示,已知△ABC与△CDA关于点O对称,过O任作直线EF分别交AD、BC于点E、F,下面的结论:(1)点E和点F;点B和点D是关于中心O的对称点;(2)直线BD必经过点O;(3)四边形ABCD是中心对称图形;(4)四边形DEOC与四边形BFOA的面积必相等;(5)△AOE与△COF成中心对称,其中正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 5个
分析:△ABC与△CDA关于点O对称是两个图形的关系,但我们将这两个图形看成一个整体,那么它就是一个关于O点的中心对称图形,故(3)正确。B与D关于O对称,图形上的两点的连线若经过中心,这两点就是对称点,同时对称点的连线必经过对称中心,所以(1)(2)都正确;从中心对称图形的性质得知,四边形DEOC与四边形BFOA是四对对称点所围成的图形,△AOE与△COF也是对称点所围成的图形,所以它们分别成中心对称,故(4)和(5)都正确。选D
例3.某同学学习了几何中的对称后,忽然想起了过去做过一道题:有一组数排成方阵,如图所示,试计算这组数的和。这个同学想,方阵就象正方形,正方形是轴对称图形,也是中心对称图形,能不能利用轴对称和中心对称的思想来解决方阵的计算问题吗?这个同学试了试,竟得到了非常巧妙的方法,你也能试试看吗?
下面将这位同学的想法告诉大家,我们一起来体验一下。
从方阵中的数看出,一条对角线上的数都是5,若把这条对角线当作轴,把正方形翻折一下,对称位置的两数之和都是10,这样方阵中数的和即可求。也可考虑:把方阵绕中心旋转180°,就得到另一方阵,再加到原来的方阵上去,就得到所有的数都是
10的方阵,这一方阵数的和亦可求。
解法一: 解法二:
此题还可引伸成解决其它数学问题。
当在求一组有规律的数的和时,经常会用到对称思想。如: 考虑: 所以
因此,数形结合是学习数学的一种重要思想方法。
例4. 一块方角形钢板(如图所示),如何用一条直线将其分为面积相等的两部分。
解析:首先考虑分形(分成n个规则图形)。 (1)该钢板可看成由上下两个矩形构成(如图所示),矩形是中心对称图形,过对称中心的任一直线把矩形分成全等的两部分,自然平分其面积,而矩形的对称中心是两条对角线的交点,因此,先作出两矩形的对称中心A、B,直线AB即为所求;
(2)该钢板同样可看成左右两矩形构成(如图所示),作出两矩形对称中心C,D,直线CD也符合要求;
(3)将钢板补成一个完整矩形(如图所示),作出大矩形对称中心E和补上一块矩形的对称中心F,直线EF既平分大矩形,又平分补充矩形的面积,于是EF平分原钢板面积。
同课章节目录
