山东省滕州市大坞中学2021-2022学年七年级下学期期中复习限时训练数学试题(word版含简略答案)
文档属性
| 名称 | 山东省滕州市大坞中学2021-2022学年七年级下学期期中复习限时训练数学试题(word版含简略答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 166.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-25 00:00:00 | ||
图片预览


文档简介
山东省滕州市大坞中学2021-2022学年度第二学期期中复习限时训练
七年级数学试题
一、单选题
1.等于( )
A. B. C. D.2022
2.下列运算,正确的是( )
A.5x2y4z÷2xy3x=5x2yz
B.(2a﹣3)(3a﹣1)=6a2﹣11a+3
C.(4x3y+6xy2﹣2xy)÷(﹣2xy)=2x2﹣3y
D.(3x﹣y)2=9x2﹣6xy﹣y2
3.如图,直线,则图中与互余的角有( )
A.2个 B.3个 C.4个 D.5个
4.如图,点E在AC的延长线上,下列条件能判断AB∥CD的是( )
A.∠1=∠2 B.∠3=∠4
C.∠D=∠DCE D.∠D+∠ACD=180°
5.已知点P为直线m外一点,点A,B,C为直线m上三点,,,,则点P到直线m的距离为( )
A.5cm B.2cm C.小于2cm D.不大于2cm
6.如图,边长为(m+2)的正方形纸片剪出一个边长为m的正方形之后余下部分又剪开拼成一个长方形(不重叠无缝隙),若拼成的长方形一边长为2,其面积是( )
A.2m+4 B.4m+4 C.m+4 D.2m+2
7.已知是完全平方式,则m的值是( )
A.8 B.±6 C.±12 D.±16
8.计算2020×2022-20212的结果是( )
A.-1 B.1 C.2021 D.-2021
9.计算:( )
A.1 B.-1 C.2 D.-2
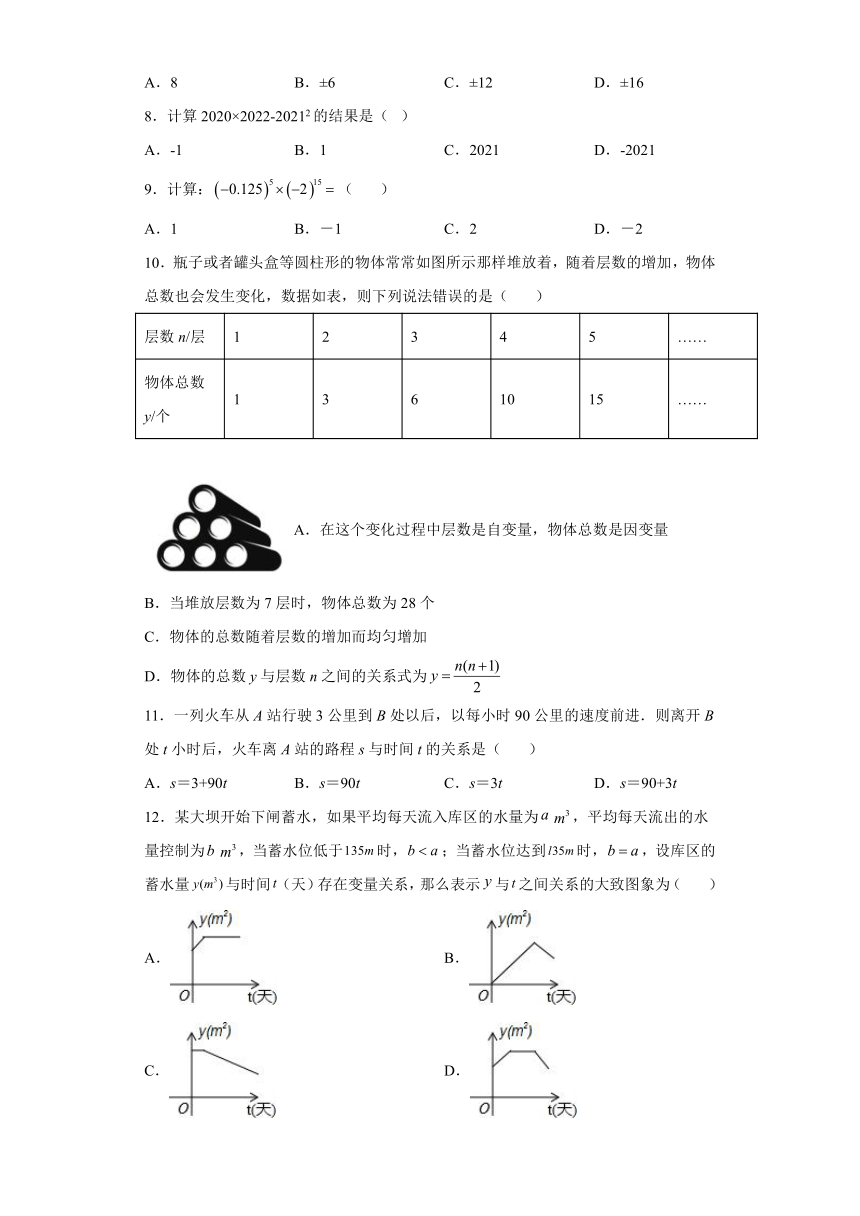
10.瓶子或者罐头盒等圆柱形的物体常常如图所示那样堆放着,随着层数的增加,物体总数也会发生变化,数据如表,则下列说法错误的是( )
层数n/层 1 2 3 4 5 ……
物体总数y/个 1 3 6 10 15 ……
A.在这个变化过程中层数是自变量,物体总数是因变量
B.当堆放层数为7层时,物体总数为28个
C.物体的总数随着层数的增加而均匀增加
D.物体的总数y与层数n之间的关系式为
11.一列火车从A站行驶3公里到B处以后,以每小时90公里的速度前进.则离开B处t小时后,火车离A站的路程s与时间t的关系是( )
A.s=3+90t B.s=90t C.s=3t D.s=90+3t
12.某大坝开始下闸蓄水,如果平均每天流入库区的水量为,平均每天流出的水量控制为,当蓄水位低于时,;当蓄水位达到时,,设库区的蓄水量与时间(天)存在变量关系,那么表示与之间关系的大致图象为( )
A. B.
C. D.
二、填空题
13.若,则的值为______.
14.若与的乘积中不含x的一次项,则实数a的值为_______________.
15.如图,将一张长方形纸片沿EF折叠后,点D、C分别落在点D′、C′位置,ED′的延长线与BC相交于点G,若∠EFG=60°,则∠1=__°.
16.已知的两边与的两边分别平行,且的度数比的度数的一半多30度,则为________度.
17.小明从家跑步到学校,接着马上原路步行回家.如图所示为小明离家的路程与时间的图像,则小明回家的速度是每分钟步行________m.
18.若,,则的值为______.
三、解答题
19.计算:
(1);
(2);
20.先化简,再求值:,其中.
21.某公空车每天的支出费用为600元,每天的乘车人数x(人)与每天利润(利润=票款收入-支出费用)y(元)的变化关系,如下表所所示(每位委文的乘车票价固定不变):
x(人) … 200 250 300 350 400 …
p(元) … -200 -100 0 100 200 …
根据表格中的数据,回答下列问题:
(1)观察表中数据可知,当乘客量达到________人以上时,该公交车才不会亏损;
(2)当一天乘客人数为500人时,利润是多少
(3)请写出公交车每天利润y(元)与每天乘车人数x(人)的关系式.
22.已知AB∥CD,线段EF分别与AB、CD相交于点E、F.
(1)如图①,当∠A=20°,∠APC=70°时,求∠C的度数;
(2)如图②,当点P在线段EF上运动时(不包括E、F两点),∠A、∠APC与∠C之间有怎样的数量?试证明你的结论.
23.观察下列各式:(x≠1)
(x﹣1)÷(x﹣1)=1;
(x2﹣1)÷(x﹣1)=x+1;
(x3﹣1)÷(x﹣1)=x2+x+1;
(x4﹣1)÷(x﹣1)=x3+x2+x+1.
(1)根据上面各式的规律可得(x5﹣1)÷(x﹣1)= ;
(2)根据上面各式的规律可得(xn+1﹣1)÷(x﹣1)= ;
(3)若1+x+x2+…+x2021=1,求x2022的值.
24.我们曾解决过这样的问题:
如图1,点O在直线AB上,OC,OD分别平分∠AOE,∠BOE,可求得∠COD=90°.(不用求解)若点O在直线AB上,∠COD=90°,OE平分∠BOC.
(1)如图2,若∠AOC=50°,求∠DOE的度数;
(2)将图2中的∠COD按图3所示的位置进行放置,写出∠AOC与∠DOE度数间的等量关系,并写明理由.
25.如图①所示, 在△ABC中,AD是三角形的高,且AD=6 cm,E是一个动点,由B向C移动,其速度与时间的变化关系如图②所示,已知BC=8 cm.
(1)求当E点在运动过程中△ABE的面积y与运动时间x之间的关系式;
(2)当E点停止后,求△ABE的面积.
试卷第1页,共3页
参考答案:
1.B 2.B 3.B 4.A 5.D 6.B
7.C 8.A 9.A 10.C 11.A 12.A
13.7
14.-5
15.120
16.60或80##80或60
17.80
18.
19.(1)
(2)
20.,2027
21.(1)300;(2)400;(3)y=2x-600
22.(1)50°
(2)∠A+∠C=∠APC,略
23.(1)x4+x3+x2+x+1
(2)xn+xn﹣1+xn﹣2+...+x+1
(3)0
24.(1);
(2)∠DOE=∠AOC.
25.(1)y=9x(0<x≤2);(2)△ABE的面积是18cm2.
答案第1页,共1页
七年级数学试题
一、单选题
1.等于( )
A. B. C. D.2022
2.下列运算,正确的是( )
A.5x2y4z÷2xy3x=5x2yz
B.(2a﹣3)(3a﹣1)=6a2﹣11a+3
C.(4x3y+6xy2﹣2xy)÷(﹣2xy)=2x2﹣3y
D.(3x﹣y)2=9x2﹣6xy﹣y2
3.如图,直线,则图中与互余的角有( )
A.2个 B.3个 C.4个 D.5个
4.如图,点E在AC的延长线上,下列条件能判断AB∥CD的是( )
A.∠1=∠2 B.∠3=∠4
C.∠D=∠DCE D.∠D+∠ACD=180°
5.已知点P为直线m外一点,点A,B,C为直线m上三点,,,,则点P到直线m的距离为( )
A.5cm B.2cm C.小于2cm D.不大于2cm
6.如图,边长为(m+2)的正方形纸片剪出一个边长为m的正方形之后余下部分又剪开拼成一个长方形(不重叠无缝隙),若拼成的长方形一边长为2,其面积是( )
A.2m+4 B.4m+4 C.m+4 D.2m+2
7.已知是完全平方式,则m的值是( )
A.8 B.±6 C.±12 D.±16
8.计算2020×2022-20212的结果是( )
A.-1 B.1 C.2021 D.-2021
9.计算:( )
A.1 B.-1 C.2 D.-2
10.瓶子或者罐头盒等圆柱形的物体常常如图所示那样堆放着,随着层数的增加,物体总数也会发生变化,数据如表,则下列说法错误的是( )
层数n/层 1 2 3 4 5 ……
物体总数y/个 1 3 6 10 15 ……
A.在这个变化过程中层数是自变量,物体总数是因变量
B.当堆放层数为7层时,物体总数为28个
C.物体的总数随着层数的增加而均匀增加
D.物体的总数y与层数n之间的关系式为
11.一列火车从A站行驶3公里到B处以后,以每小时90公里的速度前进.则离开B处t小时后,火车离A站的路程s与时间t的关系是( )
A.s=3+90t B.s=90t C.s=3t D.s=90+3t
12.某大坝开始下闸蓄水,如果平均每天流入库区的水量为,平均每天流出的水量控制为,当蓄水位低于时,;当蓄水位达到时,,设库区的蓄水量与时间(天)存在变量关系,那么表示与之间关系的大致图象为( )
A. B.
C. D.
二、填空题
13.若,则的值为______.
14.若与的乘积中不含x的一次项,则实数a的值为_______________.
15.如图,将一张长方形纸片沿EF折叠后,点D、C分别落在点D′、C′位置,ED′的延长线与BC相交于点G,若∠EFG=60°,则∠1=__°.
16.已知的两边与的两边分别平行,且的度数比的度数的一半多30度,则为________度.
17.小明从家跑步到学校,接着马上原路步行回家.如图所示为小明离家的路程与时间的图像,则小明回家的速度是每分钟步行________m.
18.若,,则的值为______.
三、解答题
19.计算:
(1);
(2);
20.先化简,再求值:,其中.
21.某公空车每天的支出费用为600元,每天的乘车人数x(人)与每天利润(利润=票款收入-支出费用)y(元)的变化关系,如下表所所示(每位委文的乘车票价固定不变):
x(人) … 200 250 300 350 400 …
p(元) … -200 -100 0 100 200 …
根据表格中的数据,回答下列问题:
(1)观察表中数据可知,当乘客量达到________人以上时,该公交车才不会亏损;
(2)当一天乘客人数为500人时,利润是多少
(3)请写出公交车每天利润y(元)与每天乘车人数x(人)的关系式.
22.已知AB∥CD,线段EF分别与AB、CD相交于点E、F.
(1)如图①,当∠A=20°,∠APC=70°时,求∠C的度数;
(2)如图②,当点P在线段EF上运动时(不包括E、F两点),∠A、∠APC与∠C之间有怎样的数量?试证明你的结论.
23.观察下列各式:(x≠1)
(x﹣1)÷(x﹣1)=1;
(x2﹣1)÷(x﹣1)=x+1;
(x3﹣1)÷(x﹣1)=x2+x+1;
(x4﹣1)÷(x﹣1)=x3+x2+x+1.
(1)根据上面各式的规律可得(x5﹣1)÷(x﹣1)= ;
(2)根据上面各式的规律可得(xn+1﹣1)÷(x﹣1)= ;
(3)若1+x+x2+…+x2021=1,求x2022的值.
24.我们曾解决过这样的问题:
如图1,点O在直线AB上,OC,OD分别平分∠AOE,∠BOE,可求得∠COD=90°.(不用求解)若点O在直线AB上,∠COD=90°,OE平分∠BOC.
(1)如图2,若∠AOC=50°,求∠DOE的度数;
(2)将图2中的∠COD按图3所示的位置进行放置,写出∠AOC与∠DOE度数间的等量关系,并写明理由.
25.如图①所示, 在△ABC中,AD是三角形的高,且AD=6 cm,E是一个动点,由B向C移动,其速度与时间的变化关系如图②所示,已知BC=8 cm.
(1)求当E点在运动过程中△ABE的面积y与运动时间x之间的关系式;
(2)当E点停止后,求△ABE的面积.
试卷第1页,共3页
参考答案:
1.B 2.B 3.B 4.A 5.D 6.B
7.C 8.A 9.A 10.C 11.A 12.A
13.7
14.-5
15.120
16.60或80##80或60
17.80
18.
19.(1)
(2)
20.,2027
21.(1)300;(2)400;(3)y=2x-600
22.(1)50°
(2)∠A+∠C=∠APC,略
23.(1)x4+x3+x2+x+1
(2)xn+xn﹣1+xn﹣2+...+x+1
(3)0
24.(1);
(2)∠DOE=∠AOC.
25.(1)y=9x(0<x≤2);(2)△ABE的面积是18cm2.
答案第1页,共1页
同课章节目录
