数学探究 杨辉三角的性质与应用(共26张PPT)
文档属性
| 名称 | 数学探究 杨辉三角的性质与应用(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-25 10:19:25 | ||
图片预览







文档简介
(共26张PPT)
杨辉三角的性质与应用
数学探究
2022
内容索引
01
02
合作探究 释疑解惑
随堂练习
课标定位素养阐释
1.探索并理解杨辉三角的性质.
2.体会杨辉三角的应用.
3.培养直观想象、数据分析、逻辑推理以及数学运算的核心素养.
合作探究 释疑解惑
探究一
杨辉三角的简单应用
【例1】 (1)杨辉三角如图所示,杨辉三角中的第5行除去两端数字1以外,均能被5整除,则具有类似性质(第n行能被n整除)的行是( )
A.第6行 B.第7行 C.第8行 D.第9行
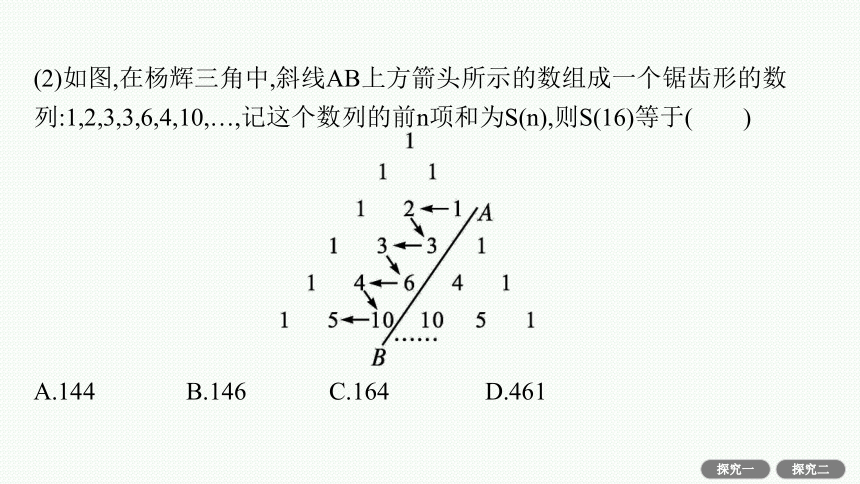
(2)如图,在杨辉三角中,斜线AB上方箭头所示的数组成一个锯齿形的数列:1,2,3,3,6,4,10,…,记这个数列的前n项和为S(n),则S(16)等于( )
A.144 B.146 C.164 D.461
解析:(1)由题意,第6行为1,6,15,20,15,6,1,第7行为1,7,21,35,35,21,7,1,故第7行除去两端数字1以外,均能被7整除.
答案:(1)B (2)C
将本例(2)改为求S(19).
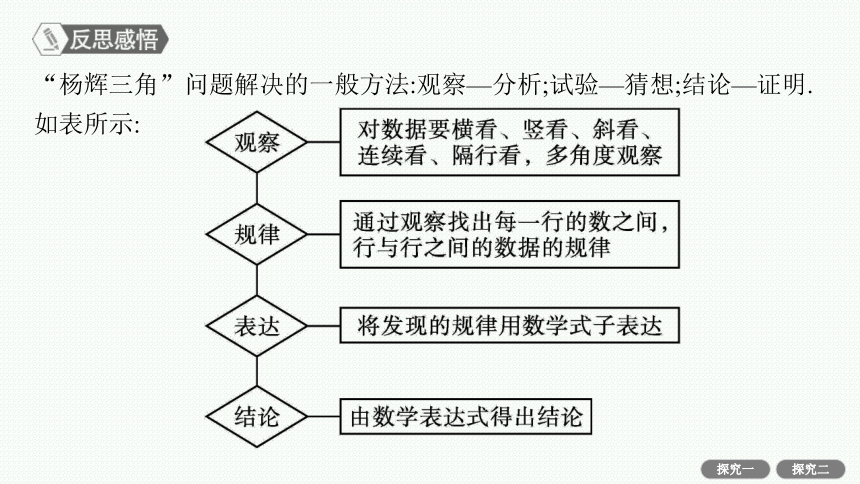
“杨辉三角”问题解决的一般方法:观察—分析;试验—猜想;结论—证明.
如表所示:
【变式训练1】 在由二项式系数所构成的杨辉三角形中,第 行中从左至右第14与第15个数的比为2∶3.
答案:34
探究二
杨辉三角在数列中的应用
【例2】 设数列{an}是{2s|s∈N}集合中的所有的数从小到大排列成的数列,将数列{an}的各项按照上小下大,左小右大的原则排成类似“杨辉三角”的图形.
(1)按图中箭头方向数字1,2,8,64,…组成一个数列{bn},求数列{bn}的通项公式;
(2)22 005是第几行的第几个数
将一等差(等比)数列重新排列成类似“杨辉三角”的图形,考查相关数列问题是杨辉三角型数列创新题的常见形式之一,这类问题主要考查重排后指定某数位置的确定或者特定行的通项公式的求法.求解关键是如何探求数列的排列规律.
【变式训练2】 一个类似“杨辉三角”的图形如图所示,第n行共有n个数,且该行的第一个数和最后一个数都是n,中间任意一个数都等于第(n-1)行与之相邻的两个数的和,an,1,an,2,…,an,n(n=1,2,3,…)分别表示第n行的第一个数,第二个数,…,第n个数.求an,2(n≥2,且n∈N)的通项公式.
解:由题图易知a2,2=2,a3,2=4,a4,2=7,a5,2=11,……
从而有a3,2-a2,2=2,
a4,2-a3,2=3,
a5,2-a4,2=4;
……
an,2-a(n-1),2=n-1.
以上(n-1)个式子相加,即可得到
随堂练习
1.根据图中的数所成的规律,a所表示的数是( )
A.2
B.4
C.6
D.8
解析:根据题图可知,每一行的第一个数和最后一个数都是1,除1以外的每个数都等于它“肩上”两个数的和,故a=3+3=6.
答案:C
2.与杨辉三角有类似性质的三角形数垒如图所示,a,b是某行的前两个数,当a=7时,b等于( )
A.20
B.21
C.22
D.23
解析:由a=7,可知b左肩上的数为6,右肩上的数为(11+5)即16,故b=6+16=22.
答案:C
3.一个类似杨辉三角的递推式如图所示,则第n(n∈N*)行的首尾两个数均为 .
解析:由1,3,5,7,9,…可知它们成等差数列,故an=2n-1.
答案:2n-1
4.如图,它满足:①第n行首尾两数均为n;②表中的递推关系类似杨辉三角,则第n(n≥2)行第2个数是 .
5.如图,在杨辉三角中,从上往下数共有n(n∈N*)行,在这些数中,非1的数之和为 .
答案:2n-2n
6.观察“莱布尼茨三角”,不难看出它与杨辉三角有类似的一条性质,即莱布尼茨三角中的每一个数都等于它左右脚下的两数之和.如图箭头所示,从第三行起将每行的第三个数 ,…按由大到小的顺序组成数列{an},求数列{an}的通项公式.
本 课 结 束
杨辉三角的性质与应用
数学探究
2022
内容索引
01
02
合作探究 释疑解惑
随堂练习
课标定位素养阐释
1.探索并理解杨辉三角的性质.
2.体会杨辉三角的应用.
3.培养直观想象、数据分析、逻辑推理以及数学运算的核心素养.
合作探究 释疑解惑
探究一
杨辉三角的简单应用
【例1】 (1)杨辉三角如图所示,杨辉三角中的第5行除去两端数字1以外,均能被5整除,则具有类似性质(第n行能被n整除)的行是( )
A.第6行 B.第7行 C.第8行 D.第9行
(2)如图,在杨辉三角中,斜线AB上方箭头所示的数组成一个锯齿形的数列:1,2,3,3,6,4,10,…,记这个数列的前n项和为S(n),则S(16)等于( )
A.144 B.146 C.164 D.461
解析:(1)由题意,第6行为1,6,15,20,15,6,1,第7行为1,7,21,35,35,21,7,1,故第7行除去两端数字1以外,均能被7整除.
答案:(1)B (2)C
将本例(2)改为求S(19).
“杨辉三角”问题解决的一般方法:观察—分析;试验—猜想;结论—证明.
如表所示:
【变式训练1】 在由二项式系数所构成的杨辉三角形中,第 行中从左至右第14与第15个数的比为2∶3.
答案:34
探究二
杨辉三角在数列中的应用
【例2】 设数列{an}是{2s|s∈N}集合中的所有的数从小到大排列成的数列,将数列{an}的各项按照上小下大,左小右大的原则排成类似“杨辉三角”的图形.
(1)按图中箭头方向数字1,2,8,64,…组成一个数列{bn},求数列{bn}的通项公式;
(2)22 005是第几行的第几个数
将一等差(等比)数列重新排列成类似“杨辉三角”的图形,考查相关数列问题是杨辉三角型数列创新题的常见形式之一,这类问题主要考查重排后指定某数位置的确定或者特定行的通项公式的求法.求解关键是如何探求数列的排列规律.
【变式训练2】 一个类似“杨辉三角”的图形如图所示,第n行共有n个数,且该行的第一个数和最后一个数都是n,中间任意一个数都等于第(n-1)行与之相邻的两个数的和,an,1,an,2,…,an,n(n=1,2,3,…)分别表示第n行的第一个数,第二个数,…,第n个数.求an,2(n≥2,且n∈N)的通项公式.
解:由题图易知a2,2=2,a3,2=4,a4,2=7,a5,2=11,……
从而有a3,2-a2,2=2,
a4,2-a3,2=3,
a5,2-a4,2=4;
……
an,2-a(n-1),2=n-1.
以上(n-1)个式子相加,即可得到
随堂练习
1.根据图中的数所成的规律,a所表示的数是( )
A.2
B.4
C.6
D.8
解析:根据题图可知,每一行的第一个数和最后一个数都是1,除1以外的每个数都等于它“肩上”两个数的和,故a=3+3=6.
答案:C
2.与杨辉三角有类似性质的三角形数垒如图所示,a,b是某行的前两个数,当a=7时,b等于( )
A.20
B.21
C.22
D.23
解析:由a=7,可知b左肩上的数为6,右肩上的数为(11+5)即16,故b=6+16=22.
答案:C
3.一个类似杨辉三角的递推式如图所示,则第n(n∈N*)行的首尾两个数均为 .
解析:由1,3,5,7,9,…可知它们成等差数列,故an=2n-1.
答案:2n-1
4.如图,它满足:①第n行首尾两数均为n;②表中的递推关系类似杨辉三角,则第n(n≥2)行第2个数是 .
5.如图,在杨辉三角中,从上往下数共有n(n∈N*)行,在这些数中,非1的数之和为 .
答案:2n-2n
6.观察“莱布尼茨三角”,不难看出它与杨辉三角有类似的一条性质,即莱布尼茨三角中的每一个数都等于它左右脚下的两数之和.如图箭头所示,从第三行起将每行的第三个数 ,…按由大到小的顺序组成数列{an},求数列{an}的通项公式.
本 课 结 束
