4.2.2等差数列的前n项和公式 课件(共30张ppt)
文档属性
| 名称 | 4.2.2等差数列的前n项和公式 课件(共30张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-25 07:02:18 | ||
图片预览










文档简介
(共30张PPT)
4.2.2等差数列的前n项和公式
1
学习目标
1.掌握等差数列前n项和公式的推导方法.(难点)
2.掌握等差数列的前n项和公式,能够运用公式解决相关问题.(重点)
3.掌握等差数列的前n项和的简单性质.(重点、难点)
2
创设情境
据说,200多年前,高斯的算术老师提出了下面的问题:
1+2+3+…+100=?
你准备怎么算呢?
3
探究新知
高斯(Gauss,1777-1855),德国数学家,近代数学的奠基者之一. 他在天文学、大地测量学、磁学、光学等领域都做出过杰出贡献.
问题1:为什么1+100=2+99=…=50+51呢?
这是巧合吗?试从数列角度给出解释.
高斯的算法:
(1+100)+(2+99)+…+(50+51)=
高斯的算法实际上解决了求等差数列:
1,2,3,…,
前100项的和问题
4
等差数列中,下标和相等的两项和相等.
设 an=n,则 a1=1,a2=2,a3=3,…
如果数列{an}是等差数列,p,q,s,t∈N*,
且 p+q=s+t,则 ap+aq=as+at
可得:
探究新知
5
问题2: 你能用上述方法计算1+2+3+… +101吗?
问题3: 你能计算1+2+3+… +n吗?
探究新知
需要对项数的奇偶进行分类讨论.
当n为偶数时,
+
6
探究新知
当n为奇数数时, n-1为偶数
+
个
问题3: 你能计算1+2+3+… +n吗?
所以对任意正整数n,都有1+2+3+… +n.
问题4:涉及对 n 分奇数、偶数进行讨论,较麻烦,能否设法避免分类讨论?
7
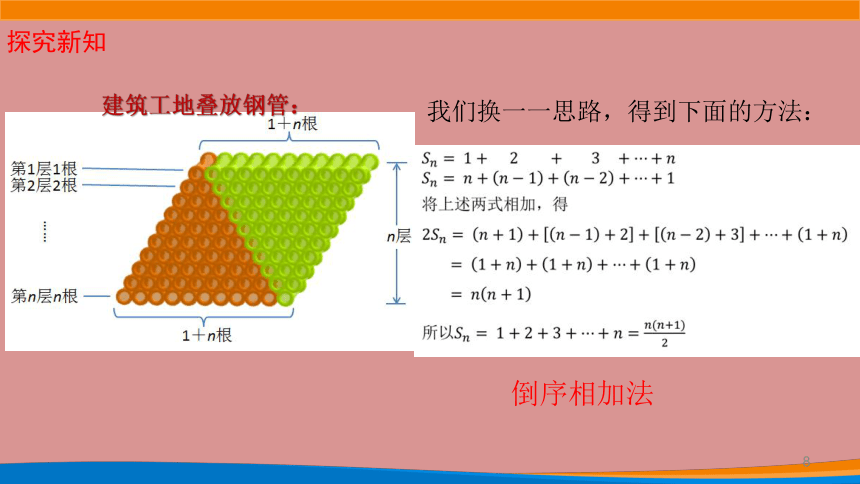
建筑工地叠放钢管:
我们换一一思路,得到下面的方法:
倒序相加法
探究新知
8
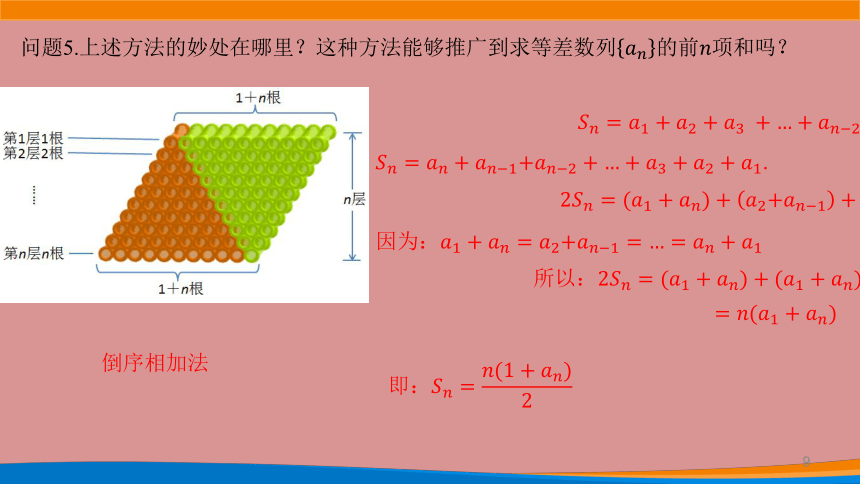
问题5.上述方法的妙处在哪里?这种方法能够推广到求等差数列的前项和吗?
倒序相加法
.
9
公式解析
功能1:已知a1,an和n,求Sn .
功能2:已知Sn,n,a1 和an中任意3个,求第4个.
10
分析:对于(1),可以直接利用公式求和;在(2)中,可以先利用a1和的值求出d ,再利用公式求和;(3)已知公式中的,和,解方程即可求得
例6.已知数列{an}是等差数列.
(1)若a1=7,=101,求;
(2)若a1=2,= ,求;
(3)若=,d= , = 5,求;
典例解析
11
解:(1)因为a1=7,=101 ,根据公式,可得
=2700.
(2)因为a1=2,= ,所以d= .根据公式,可得
=
(3)把=,d= , = 5代入,得
整理,得
解得或(舍),所以
12
等差数列中的基本计算
(1)利用基本量求值:等差数列的通项公式和前n项和公式中有五个量a1,d,n,an和Sn
这五个量可以“知三求二”.一般是利用公式列出基本量a1和d的方程组,解出a1和d,
便可解决问题.解题时注意整体代换的思想.
(2)结合等差数列的性质解题:等差数列的常用性质:
若m+n=p+q(m,n,p,q∈N*),则am+an=ap+aq,常与求和公式Sn结合使用.
13
14
例7.已知一个等差数列 前10项的和是310,前20项的和是1220.由这些条件能确定这个等差数列的首项和公差吗?
典例解析
分析 可得到两个关于的二元一次方程,解这两个二元一次方程所组成的方程组,就可以求得
解=310,=1220,
把它们代入公式
得解方程组,得
所以,由所给的条件可以确定等差数列的首项和公差。
一般地,对于等差数列,只要给定两个相互独立的条件,这个数列就完全确定。
15
典例解析
分析:将第1排到第20排的座位数依次排成一列,构成数列{an},设数列{an}的前项和为。由题意可知, {an}是等差数列,且公差及前20项和已知,所以可利用等差数列的前项和公式求首项。
例8.某校新建一个报告厅,要求容纳800个座位,报告厅共有20排座位,从第2排起后一排都比前一排多两个座位. 问第1排应安排多少个座位?
16
典例解析
例8.某校新建一个报告厅,要求容纳800个座位,报告厅共有20排座位,从第2排起后一排都比前一排多两个座位. 问第1排应安排多少个座位?
解:设报告厅的座位从第1排到第20排,各排的座位数依次排成一列,构成数列{an},其前n项和为Sn.
根据题意,数列{an}是一个公差为2的等差数列,且S20=800.
由
a121
因此,第1排应安排21个座位。
17
跟踪训练 某抗洪指挥部接到预报,24小时后有一洪峰到达,为确保安全,指挥部决定在洪峰到来之前临时筑一道堤坝作为第二道防线.经计算,除现有的参战军民连续奋战外,还需调用20台同型号翻斗车,平均每辆车工作24小时.从各地紧急抽调的同型号翻斗车目前只有一辆投入使用,每隔20分钟能有一辆翻斗车到达,一共可调集25辆,那么在24小时内能否构筑成第二道防线?
18
跟踪训练 某抗洪指挥部接到预报,24小时后有一洪峰到达,为确保安全,指挥部决定在洪峰到来之前临时筑一道堤坝作为第二道防线.经计算,除现有的参战军民连续奋战外,还需调用20台同型号翻斗车,平均每辆车工作24小时.从各地紧急抽调的同型号翻斗车目前只有一辆投入使用,每隔20分钟能有一辆翻斗车到达,一共可调集25辆,那么在24小时内能否构筑成第二道防线?
19
典例解析
分析
数项的和。
例9.已知等差数列{an}的前n项和为Sn,若a1=10,公差d=-2,Sn是否存在最大值?若存在,求Sn的最大值及取得最大值时n的值;若不存在,请说明理由.
另一方面,等差数列的前n项和公式可写成,
所以当时,可以看成二次函数,当=时函数值。如图,当时,关于的图像是一条开口向下的抛物线上的一些点,因此,可以利用二次函数求相应的,的值。
20
解法1.由d=-2,得an+1-an=-2<0,得an+1<an ,所以{an}是递减数列.
由a1=10,d=-2,得an=10+(n-1)×(-2) =-2n+12.
可知,当n<6时,an>0;
当n=6时,an=0;
当n>6时,an<0.
所以, S1<S2<…<S5=S6> S7>…
也就是说,当n=5或6时,Sn最大.
因为 =30
所以Sn的最大值为30.
例9.已知等差数列{an}的前n项和为Sn,若a1=10,公差d=-2,Sn是否存在最大值?若存在,求Sn的最大值及取得最大值时n的值;若不存在,请说明理由.
21
典例解析
例9.已知等差数列{an}的前n项和为Sn,若a1=10,公差d=-2,Sn是否存在最大值?若存在,求Sn的最大值及取得最大值时n的值;若不存在,请说明理由.
解法2:因为由a1=10,d=-2,
因为
所以,当n取与最接近的整数,
即5或6时,Sn最大,最大值为30.
22
等差数列前n项和性质
1).将等差数列前n项和公式 看作是
一个关于n的函数,这个函数有什么特点?
当d≠0时,Sn是常数项为零的二次函数
则 Sn=An2+Bn
令
(过原点)
23
当堂达标
24
当堂达标
25
当堂达标
26
当堂达标
27
当堂达标
28
课堂小结
29
再会!
30
4.2.2等差数列的前n项和公式
1
学习目标
1.掌握等差数列前n项和公式的推导方法.(难点)
2.掌握等差数列的前n项和公式,能够运用公式解决相关问题.(重点)
3.掌握等差数列的前n项和的简单性质.(重点、难点)
2
创设情境
据说,200多年前,高斯的算术老师提出了下面的问题:
1+2+3+…+100=?
你准备怎么算呢?
3
探究新知
高斯(Gauss,1777-1855),德国数学家,近代数学的奠基者之一. 他在天文学、大地测量学、磁学、光学等领域都做出过杰出贡献.
问题1:为什么1+100=2+99=…=50+51呢?
这是巧合吗?试从数列角度给出解释.
高斯的算法:
(1+100)+(2+99)+…+(50+51)=
高斯的算法实际上解决了求等差数列:
1,2,3,…,
前100项的和问题
4
等差数列中,下标和相等的两项和相等.
设 an=n,则 a1=1,a2=2,a3=3,…
如果数列{an}是等差数列,p,q,s,t∈N*,
且 p+q=s+t,则 ap+aq=as+at
可得:
探究新知
5
问题2: 你能用上述方法计算1+2+3+… +101吗?
问题3: 你能计算1+2+3+… +n吗?
探究新知
需要对项数的奇偶进行分类讨论.
当n为偶数时,
+
6
探究新知
当n为奇数数时, n-1为偶数
+
个
问题3: 你能计算1+2+3+… +n吗?
所以对任意正整数n,都有1+2+3+… +n.
问题4:涉及对 n 分奇数、偶数进行讨论,较麻烦,能否设法避免分类讨论?
7
建筑工地叠放钢管:
我们换一一思路,得到下面的方法:
倒序相加法
探究新知
8
问题5.上述方法的妙处在哪里?这种方法能够推广到求等差数列的前项和吗?
倒序相加法
.
9
公式解析
功能1:已知a1,an和n,求Sn .
功能2:已知Sn,n,a1 和an中任意3个,求第4个.
10
分析:对于(1),可以直接利用公式求和;在(2)中,可以先利用a1和的值求出d ,再利用公式求和;(3)已知公式中的,和,解方程即可求得
例6.已知数列{an}是等差数列.
(1)若a1=7,=101,求;
(2)若a1=2,= ,求;
(3)若=,d= , = 5,求;
典例解析
11
解:(1)因为a1=7,=101 ,根据公式,可得
=2700.
(2)因为a1=2,= ,所以d= .根据公式,可得
=
(3)把=,d= , = 5代入,得
整理,得
解得或(舍),所以
12
等差数列中的基本计算
(1)利用基本量求值:等差数列的通项公式和前n项和公式中有五个量a1,d,n,an和Sn
这五个量可以“知三求二”.一般是利用公式列出基本量a1和d的方程组,解出a1和d,
便可解决问题.解题时注意整体代换的思想.
(2)结合等差数列的性质解题:等差数列的常用性质:
若m+n=p+q(m,n,p,q∈N*),则am+an=ap+aq,常与求和公式Sn结合使用.
13
14
例7.已知一个等差数列 前10项的和是310,前20项的和是1220.由这些条件能确定这个等差数列的首项和公差吗?
典例解析
分析 可得到两个关于的二元一次方程,解这两个二元一次方程所组成的方程组,就可以求得
解=310,=1220,
把它们代入公式
得解方程组,得
所以,由所给的条件可以确定等差数列的首项和公差。
一般地,对于等差数列,只要给定两个相互独立的条件,这个数列就完全确定。
15
典例解析
分析:将第1排到第20排的座位数依次排成一列,构成数列{an},设数列{an}的前项和为。由题意可知, {an}是等差数列,且公差及前20项和已知,所以可利用等差数列的前项和公式求首项。
例8.某校新建一个报告厅,要求容纳800个座位,报告厅共有20排座位,从第2排起后一排都比前一排多两个座位. 问第1排应安排多少个座位?
16
典例解析
例8.某校新建一个报告厅,要求容纳800个座位,报告厅共有20排座位,从第2排起后一排都比前一排多两个座位. 问第1排应安排多少个座位?
解:设报告厅的座位从第1排到第20排,各排的座位数依次排成一列,构成数列{an},其前n项和为Sn.
根据题意,数列{an}是一个公差为2的等差数列,且S20=800.
由
a121
因此,第1排应安排21个座位。
17
跟踪训练 某抗洪指挥部接到预报,24小时后有一洪峰到达,为确保安全,指挥部决定在洪峰到来之前临时筑一道堤坝作为第二道防线.经计算,除现有的参战军民连续奋战外,还需调用20台同型号翻斗车,平均每辆车工作24小时.从各地紧急抽调的同型号翻斗车目前只有一辆投入使用,每隔20分钟能有一辆翻斗车到达,一共可调集25辆,那么在24小时内能否构筑成第二道防线?
18
跟踪训练 某抗洪指挥部接到预报,24小时后有一洪峰到达,为确保安全,指挥部决定在洪峰到来之前临时筑一道堤坝作为第二道防线.经计算,除现有的参战军民连续奋战外,还需调用20台同型号翻斗车,平均每辆车工作24小时.从各地紧急抽调的同型号翻斗车目前只有一辆投入使用,每隔20分钟能有一辆翻斗车到达,一共可调集25辆,那么在24小时内能否构筑成第二道防线?
19
典例解析
分析
数项的和。
例9.已知等差数列{an}的前n项和为Sn,若a1=10,公差d=-2,Sn是否存在最大值?若存在,求Sn的最大值及取得最大值时n的值;若不存在,请说明理由.
另一方面,等差数列的前n项和公式可写成,
所以当时,可以看成二次函数,当=时函数值。如图,当时,关于的图像是一条开口向下的抛物线上的一些点,因此,可以利用二次函数求相应的,的值。
20
解法1.由d=-2,得an+1-an=-2<0,得an+1<an ,所以{an}是递减数列.
由a1=10,d=-2,得an=10+(n-1)×(-2) =-2n+12.
可知,当n<6时,an>0;
当n=6时,an=0;
当n>6时,an<0.
所以, S1<S2<…<S5=S6> S7>…
也就是说,当n=5或6时,Sn最大.
因为 =30
所以Sn的最大值为30.
例9.已知等差数列{an}的前n项和为Sn,若a1=10,公差d=-2,Sn是否存在最大值?若存在,求Sn的最大值及取得最大值时n的值;若不存在,请说明理由.
21
典例解析
例9.已知等差数列{an}的前n项和为Sn,若a1=10,公差d=-2,Sn是否存在最大值?若存在,求Sn的最大值及取得最大值时n的值;若不存在,请说明理由.
解法2:因为由a1=10,d=-2,
因为
所以,当n取与最接近的整数,
即5或6时,Sn最大,最大值为30.
22
等差数列前n项和性质
1).将等差数列前n项和公式 看作是
一个关于n的函数,这个函数有什么特点?
当d≠0时,Sn是常数项为零的二次函数
则 Sn=An2+Bn
令
(过原点)
23
当堂达标
24
当堂达标
25
当堂达标
26
当堂达标
27
当堂达标
28
课堂小结
29
再会!
30
