五年级下学期数学第二单元《因数与倍数》整理与复习课件(共14张PPT)
文档属性
| 名称 | 五年级下学期数学第二单元《因数与倍数》整理与复习课件(共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-24 00:00:00 | ||
图片预览

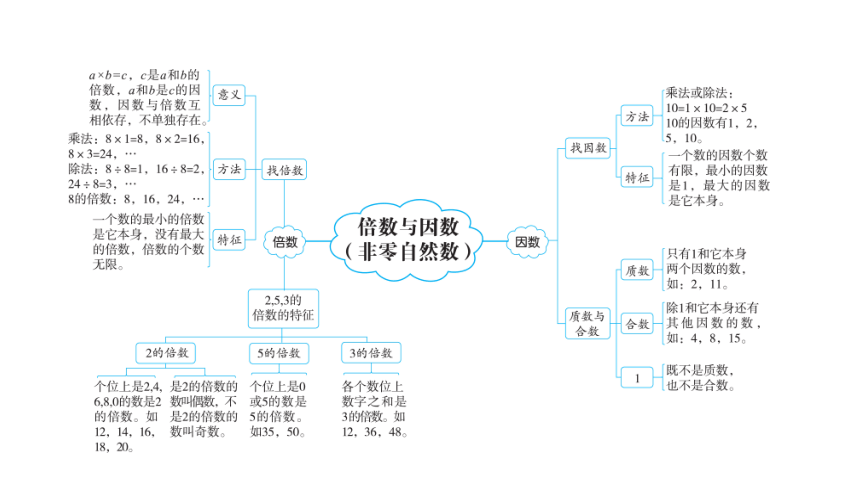





文档简介
(共14张PPT)
第二单元《因数与倍数》整理与复习
人教版五年级下册
知识梳理
1.因数和倍数
(1)在整数除法中,如果商是整数而没有余数,我们就说_________是
_______的_______,_______是_________的_______。因数和倍数是___________的。
(2)一个数的因数的个数是_________,_______的因数是____,_______的因数是它_______。
(3)一个数的倍数的个数是_________,_______的倍数是它_______,没有最大的倍数。
被除数
除数
倍数
除数
被除数
因数
相互依存
有限的
最小
1
最大
本身
无限的
最小
本身
(4)为了方便,在研究_____________时,我们所说的数是指_________(一般不包括0)。
【注意事项】如果_________都是_________的_______,那么这_________________也是这个数的_______,推广为:如果_________都是_________的_______,那么_________________也是这个数的_______。
因数和倍数
自然数
两个数
一个数
倍数
两个数的和或差
倍数
个数
一个数
倍数
个数的和或差
倍数
2.2、5、3的倍数的特征
(1)整数中,是 __________的数叫作_______(0也是偶数),_______________的数叫作_______。
2的倍数
偶数
不是2的倍数
奇数
(2)_______上______________________都是2的倍数。
(3)_______上_____________都是5的倍数。
(4)一个数_________________是3的倍数,它就是3的倍数。
【提示】_________中不是_______就是_______,_______的_______是____,_______的_______是____,______________________,______________________。
个位
是0、2、4、6、8的数
个位
是5或0的数
各位上的数的和
自然数
奇数
偶数
最小
偶数
0
最小
奇数
1
相邻的两个偶数相差2
相邻的两个奇数相差2
3.质数和合数
(1)一个数,如果只有 ____和它_______两个因数,那么这样的数叫作
1
本身
_______(或素数)。
(2)一个数,除了____和它_______还有___________,那么这样的数叫作_______。
(3)____既___________也___________。
(4)和的奇偶性:奇数+奇数=偶数 奇数+偶数=奇数
偶数+偶数=偶数
(5)奇数-偶数=奇数 奇数-奇数=偶数
偶数-偶数=偶数 奇数×奇数=奇数
偶数×偶数=偶数 偶数×奇数=偶数
质数
1
本身
别的因数
合数
1
不是质数
不是合数
【注意】最小的质数是2,最小的合数是4。
【重点提示】____是_______中唯一的_______。
2
偶数
质数
从资料中理解奇数和偶数,质数和合数,及2、5、3的倍数的特征
1. 第29届夏季奥运会于2008年8月8日在中国首都北京开幕,这次奥运会火炬接力活动以“点燃激情,传递梦想”为口号,参加的火炬手有21780人,是迄今为止参加人数最多的一次奥运圣火传递。1986年,国际奥委会全会决定将冬季奥运会和夏季奥运会从1994年起分开,每2年间隔举行,1992
倍数 因数
找倍数用乘法,如2的倍数:2×1=2,2×2=4,2×3=6…… 找因数要一对一对地找。如找12的因数:12=( )×( )=(
)×( )=( )×( ),所以12的因数有( )。
一个数的倍数的个数是( )的。(填“有限”或“无限”) 一个数的因数的个数是( )的。(填“有限”或“无限”)
1,2,3,4,6,12
1.理解因数、倍数的概念,并牢记2,5,3的倍数的特征。
横排:1
12
2
6
3
4
无限
有限
年冬季奥运会是最后一届与夏季奥运会同年举行的冬奥会。冬季奥运会自1924年开始第1届,截至2018年共举办了23届,每四年一届。第24届冬季奥运会将于2022年2月4日在中国北京和张家口联合举办。中国北京是世界上首个举办冬夏奥运会的城市。
在上面资料的数据中,
(1) 偶数有:______________________________________________________________________________;
奇数有:______________。
2008、 、 、 、 、 、 、 、2018、 、2022、
、 、
(2) 质数有:______________;合数有:_______________________________________________________________________。
(3) 3的倍数有:___________________________________。
、 、 、 、2022
(4) 5的倍数有:________。
(5) 同时是2、 的倍数的有:___________________________________。
、 、 、 、2022
(6) 同时是2、 、 的倍数的有:________。
、 、
2008、 、 、 、 、 、 、2018、 、2022、
结合生活中的情景理解和的奇偶性
2. 大课间活动时,五(4)班42名学生计划分成两队,如果第一队的人数为奇数,那么第二队的人数是( );如果第一队的人数为偶数,那么第二队的人数是( )。(填“奇数”或“偶数”)
奇数
偶数
(1) 结合你对和的奇偶性的理解,写出你判断是奇数还是偶数的理由。
[答案] 因为奇数+奇数=偶数,偶数+偶数=偶数,所以42人分成2组,若其中一组是奇数,另一组就是奇数;若其中一组是偶数,另一组就是偶数。
(2) 如果分成小组,让组数和每组人数同时具有下面的特征,请你写出分组方案。
①偶数与奇数 ②合数与质数 ③互为质数 ④相邻自然数
[答案] 分成6组,每组7人或分成7组,每组6人。
综合应用,在规律中理解奇数和偶数
3. 斐波那契数列又称黄金分割数列,因数学家斐波那契以兔子繁殖为例子而引入,故又称为“兔子数列”。下面这样一列数就是斐波那契数列: 、 、 、 、 、 、 、 、
(1) 这一列数接下来的三个数分别是几?
[答案] 这一列数接下来的三个数分别是55、 、 。
(2) 这一列数中的第100个数是奇数还是偶数?写出你的判断理由。
[答案] (组) (个)
第100个数是奇数。
通过观察发现,这列数从第3个数开始,每个数都等于前两个数之和。并且按照奇数、奇数、偶数的顺序循环排列,所以求出第100个数是第几组的第几个数,就可以判断出是奇数还是偶数。
第二单元《因数与倍数》整理与复习
人教版五年级下册
知识梳理
1.因数和倍数
(1)在整数除法中,如果商是整数而没有余数,我们就说_________是
_______的_______,_______是_________的_______。因数和倍数是___________的。
(2)一个数的因数的个数是_________,_______的因数是____,_______的因数是它_______。
(3)一个数的倍数的个数是_________,_______的倍数是它_______,没有最大的倍数。
被除数
除数
倍数
除数
被除数
因数
相互依存
有限的
最小
1
最大
本身
无限的
最小
本身
(4)为了方便,在研究_____________时,我们所说的数是指_________(一般不包括0)。
【注意事项】如果_________都是_________的_______,那么这_________________也是这个数的_______,推广为:如果_________都是_________的_______,那么_________________也是这个数的_______。
因数和倍数
自然数
两个数
一个数
倍数
两个数的和或差
倍数
个数
一个数
倍数
个数的和或差
倍数
2.2、5、3的倍数的特征
(1)整数中,是 __________的数叫作_______(0也是偶数),_______________的数叫作_______。
2的倍数
偶数
不是2的倍数
奇数
(2)_______上______________________都是2的倍数。
(3)_______上_____________都是5的倍数。
(4)一个数_________________是3的倍数,它就是3的倍数。
【提示】_________中不是_______就是_______,_______的_______是____,_______的_______是____,______________________,______________________。
个位
是0、2、4、6、8的数
个位
是5或0的数
各位上的数的和
自然数
奇数
偶数
最小
偶数
0
最小
奇数
1
相邻的两个偶数相差2
相邻的两个奇数相差2
3.质数和合数
(1)一个数,如果只有 ____和它_______两个因数,那么这样的数叫作
1
本身
_______(或素数)。
(2)一个数,除了____和它_______还有___________,那么这样的数叫作_______。
(3)____既___________也___________。
(4)和的奇偶性:奇数+奇数=偶数 奇数+偶数=奇数
偶数+偶数=偶数
(5)奇数-偶数=奇数 奇数-奇数=偶数
偶数-偶数=偶数 奇数×奇数=奇数
偶数×偶数=偶数 偶数×奇数=偶数
质数
1
本身
别的因数
合数
1
不是质数
不是合数
【注意】最小的质数是2,最小的合数是4。
【重点提示】____是_______中唯一的_______。
2
偶数
质数
从资料中理解奇数和偶数,质数和合数,及2、5、3的倍数的特征
1. 第29届夏季奥运会于2008年8月8日在中国首都北京开幕,这次奥运会火炬接力活动以“点燃激情,传递梦想”为口号,参加的火炬手有21780人,是迄今为止参加人数最多的一次奥运圣火传递。1986年,国际奥委会全会决定将冬季奥运会和夏季奥运会从1994年起分开,每2年间隔举行,1992
倍数 因数
找倍数用乘法,如2的倍数:2×1=2,2×2=4,2×3=6…… 找因数要一对一对地找。如找12的因数:12=( )×( )=(
)×( )=( )×( ),所以12的因数有( )。
一个数的倍数的个数是( )的。(填“有限”或“无限”) 一个数的因数的个数是( )的。(填“有限”或“无限”)
1,2,3,4,6,12
1.理解因数、倍数的概念,并牢记2,5,3的倍数的特征。
横排:1
12
2
6
3
4
无限
有限
年冬季奥运会是最后一届与夏季奥运会同年举行的冬奥会。冬季奥运会自1924年开始第1届,截至2018年共举办了23届,每四年一届。第24届冬季奥运会将于2022年2月4日在中国北京和张家口联合举办。中国北京是世界上首个举办冬夏奥运会的城市。
在上面资料的数据中,
(1) 偶数有:______________________________________________________________________________;
奇数有:______________。
2008、 、 、 、 、 、 、 、2018、 、2022、
、 、
(2) 质数有:______________;合数有:_______________________________________________________________________。
(3) 3的倍数有:___________________________________。
、 、 、 、2022
(4) 5的倍数有:________。
(5) 同时是2、 的倍数的有:___________________________________。
、 、 、 、2022
(6) 同时是2、 、 的倍数的有:________。
、 、
2008、 、 、 、 、 、 、2018、 、2022、
结合生活中的情景理解和的奇偶性
2. 大课间活动时,五(4)班42名学生计划分成两队,如果第一队的人数为奇数,那么第二队的人数是( );如果第一队的人数为偶数,那么第二队的人数是( )。(填“奇数”或“偶数”)
奇数
偶数
(1) 结合你对和的奇偶性的理解,写出你判断是奇数还是偶数的理由。
[答案] 因为奇数+奇数=偶数,偶数+偶数=偶数,所以42人分成2组,若其中一组是奇数,另一组就是奇数;若其中一组是偶数,另一组就是偶数。
(2) 如果分成小组,让组数和每组人数同时具有下面的特征,请你写出分组方案。
①偶数与奇数 ②合数与质数 ③互为质数 ④相邻自然数
[答案] 分成6组,每组7人或分成7组,每组6人。
综合应用,在规律中理解奇数和偶数
3. 斐波那契数列又称黄金分割数列,因数学家斐波那契以兔子繁殖为例子而引入,故又称为“兔子数列”。下面这样一列数就是斐波那契数列: 、 、 、 、 、 、 、 、
(1) 这一列数接下来的三个数分别是几?
[答案] 这一列数接下来的三个数分别是55、 、 。
(2) 这一列数中的第100个数是奇数还是偶数?写出你的判断理由。
[答案] (组) (个)
第100个数是奇数。
通过观察发现,这列数从第3个数开始,每个数都等于前两个数之和。并且按照奇数、奇数、偶数的顺序循环排列,所以求出第100个数是第几组的第几个数,就可以判断出是奇数还是偶数。
