7.3万有引力理论的成就(共25张ppt)
文档属性
| 名称 | 7.3万有引力理论的成就(共25张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 646.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-04-24 14:06:37 | ||
图片预览






文档简介
(共25张PPT)
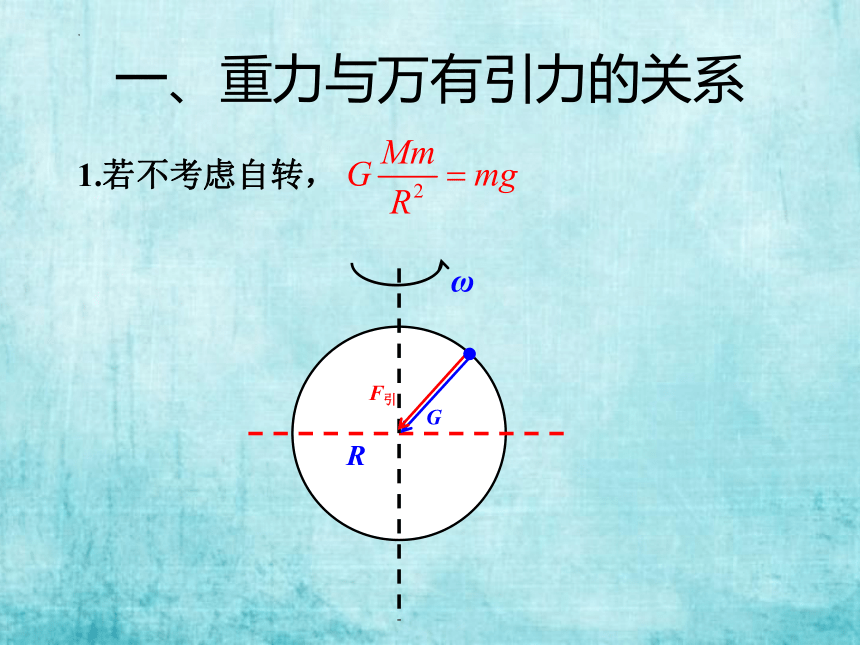
1.内容:
自然界中任何两个物体都相互吸引,引力的大小与物体的质量m1和m2的乘积成正比,与它们之间距离r的二次方成反比。
2.公式:
引力常量G=6.67×10-11 N·m2/kg2
3.条件:
质点或均质球体
m2
m1
F
F
r
万有引力定律
第三节、万有引力理论的成就
ω
R
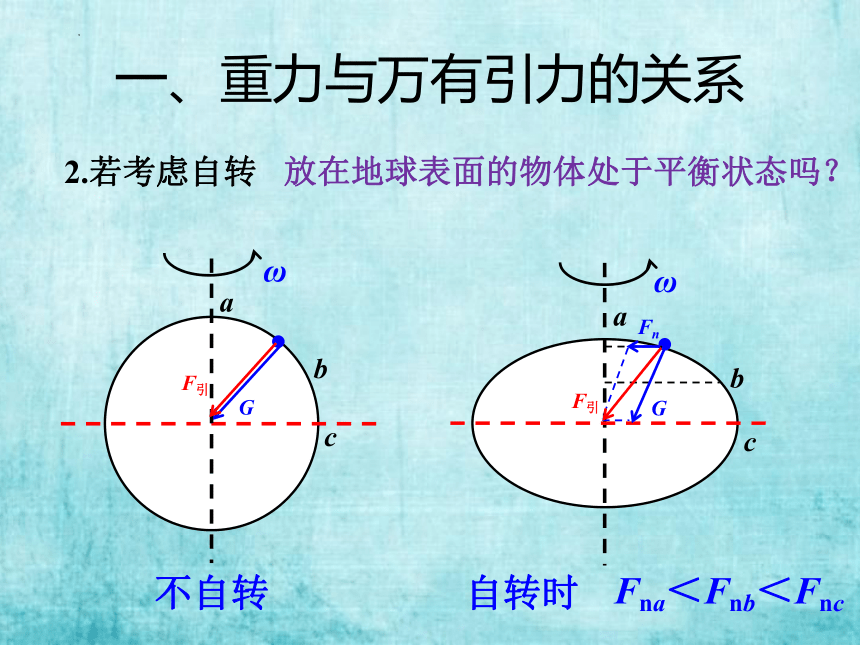
一、重力与万有引力的关系
1.若不考虑自转,
G
F引
ω
a
b
c
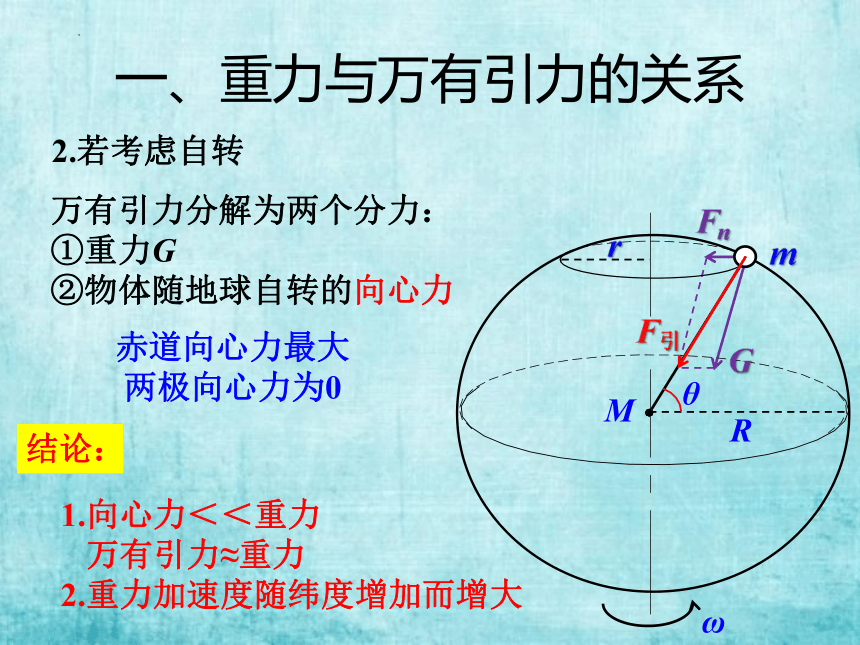
一、重力与万有引力的关系
G
不自转
a
b
c
Fna<Fnb<Fnc
自转时
ω
Fn
F引
F引
2.若考虑自转
放在地球表面的物体处于平衡状态吗?
G
一、重力与万有引力的关系
地球其近似为两级略扁,赤道略鼓的椭圆
2.若考虑自转
北极
南极
一、重力与万有引力的关系
2.若考虑自转
万有引力分解为两个分力:
①重力G
②物体随地球自转的向心力
R
M
θ
m
ω
r
Fn
F引
G
赤道向心力最大
两极向心力为0
1.向心力<<重力
万有引力≈重力
2.重力加速度随纬度增加而增大
结论:
二、称量地球的质量
——阿基米德
“给我一个支点,我可以撬动地球。”
测量巨大的天体质量只能采用间接的方法.
万有引力理论给我们提供了重要的启示和解决方案。
卡文迪许是如何“称量地球的质量”的呢
二、称量地球的质量
当时已知的事实
地表重力加速度: g = 9.8m/s2
地球半径: R = 6400×103m
引力常量G G=6.67×10-11 N·m2/kg2
二、称量地球的质量
若不考虑地球自转的影响
其中g、R在卡文迪许之前已经知道,而卡文迪许测出G后,就意味着我们也测出了地球的质量。
卡文迪许被称为“第一个称量地球质量的人”
M=6.0×1024kg
二、称量地球的质量
科学真是迷人。根据零星的事实,增加
一点猜想,竟能赢得那么多的收获!
——马克·吐温
三、计算天体质量
如何计算太阳的质量?
需要测量哪些物理量?
①某绕日行星v、r
②或w、r
③或T、r
最容易
三、计算天体质量
M=2.0×1030kg
三、计算天体质量
不同行星与太阳的距离r和绕太阳公转的周期T都是
不同的。上面这个公式能保证计算结果一致吗?
根据开普勒第三定律:
k只和中心天体(太阳)的质量有关。
分析:
三、计算天体质量
月球绕地球运行的周期T=27.3天
月球与地球的距离r=3.84×108m
M=6×1024kg
计算地球的质量,除了一开始的方法外,
有没有其它的办法?
三、计算天体质量
法一:
物体在天体表面时受到的
重力等于万有引力
g ——天体表面的重力加速度
R——天体的半径
总结:
三、计算天体质量
法二:
利用天体的卫星,所受万有引力提供向心力
r——轨道的半径
与卫星质量m无关。只能测得中心天体的质量,不能求出环绕天体的质量
总结:
M——中心天体的质量
本章解题思路
中心天体
环绕天体
心间距
①
②
③
④
⑤
1.根据题目条件联立各式
2.环绕天体质量m无法求出
环绕
表面
当R=r时,mg
练习
如何求解月球的质量?
法一:
得知月球表面的g和月球半径R
法二:
得知环绕月球卫星的轨道半径r及线速度v或角速度或周期T
M=7.3×10 kg
四、计算天体密度
球形体积表达式:
密度:
法一:
四、计算天体密度
法二:
当r≈R时(即低轨道卫星)
只需T就能求得ρ
四、计算天体密度
月=3.35×103kg/m3
=5.51×103kg/m3
1.408×103kg/m3
五、发现未知天体
海王星
在1781年发现的第七个行星—天王星的运动轨道,总是同根据万有引力定律计算出来的有一定偏离.当时有人预测,肯定在其轨道外还有一颗未发现的新星,这就是后来发现的第八大行星—海王星.
五、发现未知天体
亚当斯
勒维耶
19世纪初,两人在互不知晓的情况下分别进行了整整两年的工作。1845年亚当斯先算出结果,但格林尼治天文台却把他的论文束之高阁。
1846年9月18日,勒威耶把结果寄到了柏林,却受到了重视。柏林天文台的伽勒于1846年9月23日晚就进行了搜索,并且在离勒威耶预报位置不远的地方发现了这颗新行星。 海王星的发现使哥白尼学说和牛顿力学得到了最好的证明。
五、发现未知天体
海王星发现之后,人们发现它的轨道也与理论计算的不一致。于是几位学者用亚当斯和勒维耶的方法预言另一颗新行星的存在.
在预言提出之后,1930年,汤博发现了太阳系的后来曾被称为第九大行星的冥王星。
五、发现未知天体
海王星、冥王星的发现最终确立了万有引力定律的地位,也成为科学史上的美谈。诺贝尔物理学奖获得者,物理学家冯·劳厄说:
“没有任何东西向牛顿引力理论对行星轨道的计算那样,如此有力地树起人们对年轻的物理学的尊敬。从此以后,这门自然科学成了巨大的精神王国…… ”
1.内容:
自然界中任何两个物体都相互吸引,引力的大小与物体的质量m1和m2的乘积成正比,与它们之间距离r的二次方成反比。
2.公式:
引力常量G=6.67×10-11 N·m2/kg2
3.条件:
质点或均质球体
m2
m1
F
F
r
万有引力定律
第三节、万有引力理论的成就
ω
R
一、重力与万有引力的关系
1.若不考虑自转,
G
F引
ω
a
b
c
一、重力与万有引力的关系
G
不自转
a
b
c
Fna<Fnb<Fnc
自转时
ω
Fn
F引
F引
2.若考虑自转
放在地球表面的物体处于平衡状态吗?
G
一、重力与万有引力的关系
地球其近似为两级略扁,赤道略鼓的椭圆
2.若考虑自转
北极
南极
一、重力与万有引力的关系
2.若考虑自转
万有引力分解为两个分力:
①重力G
②物体随地球自转的向心力
R
M
θ
m
ω
r
Fn
F引
G
赤道向心力最大
两极向心力为0
1.向心力<<重力
万有引力≈重力
2.重力加速度随纬度增加而增大
结论:
二、称量地球的质量
——阿基米德
“给我一个支点,我可以撬动地球。”
测量巨大的天体质量只能采用间接的方法.
万有引力理论给我们提供了重要的启示和解决方案。
卡文迪许是如何“称量地球的质量”的呢
二、称量地球的质量
当时已知的事实
地表重力加速度: g = 9.8m/s2
地球半径: R = 6400×103m
引力常量G G=6.67×10-11 N·m2/kg2
二、称量地球的质量
若不考虑地球自转的影响
其中g、R在卡文迪许之前已经知道,而卡文迪许测出G后,就意味着我们也测出了地球的质量。
卡文迪许被称为“第一个称量地球质量的人”
M=6.0×1024kg
二、称量地球的质量
科学真是迷人。根据零星的事实,增加
一点猜想,竟能赢得那么多的收获!
——马克·吐温
三、计算天体质量
如何计算太阳的质量?
需要测量哪些物理量?
①某绕日行星v、r
②或w、r
③或T、r
最容易
三、计算天体质量
M=2.0×1030kg
三、计算天体质量
不同行星与太阳的距离r和绕太阳公转的周期T都是
不同的。上面这个公式能保证计算结果一致吗?
根据开普勒第三定律:
k只和中心天体(太阳)的质量有关。
分析:
三、计算天体质量
月球绕地球运行的周期T=27.3天
月球与地球的距离r=3.84×108m
M=6×1024kg
计算地球的质量,除了一开始的方法外,
有没有其它的办法?
三、计算天体质量
法一:
物体在天体表面时受到的
重力等于万有引力
g ——天体表面的重力加速度
R——天体的半径
总结:
三、计算天体质量
法二:
利用天体的卫星,所受万有引力提供向心力
r——轨道的半径
与卫星质量m无关。只能测得中心天体的质量,不能求出环绕天体的质量
总结:
M——中心天体的质量
本章解题思路
中心天体
环绕天体
心间距
①
②
③
④
⑤
1.根据题目条件联立各式
2.环绕天体质量m无法求出
环绕
表面
当R=r时,mg
练习
如何求解月球的质量?
法一:
得知月球表面的g和月球半径R
法二:
得知环绕月球卫星的轨道半径r及线速度v或角速度或周期T
M=7.3×10 kg
四、计算天体密度
球形体积表达式:
密度:
法一:
四、计算天体密度
法二:
当r≈R时(即低轨道卫星)
只需T就能求得ρ
四、计算天体密度
月=3.35×103kg/m3
=5.51×103kg/m3
1.408×103kg/m3
五、发现未知天体
海王星
在1781年发现的第七个行星—天王星的运动轨道,总是同根据万有引力定律计算出来的有一定偏离.当时有人预测,肯定在其轨道外还有一颗未发现的新星,这就是后来发现的第八大行星—海王星.
五、发现未知天体
亚当斯
勒维耶
19世纪初,两人在互不知晓的情况下分别进行了整整两年的工作。1845年亚当斯先算出结果,但格林尼治天文台却把他的论文束之高阁。
1846年9月18日,勒威耶把结果寄到了柏林,却受到了重视。柏林天文台的伽勒于1846年9月23日晚就进行了搜索,并且在离勒威耶预报位置不远的地方发现了这颗新行星。 海王星的发现使哥白尼学说和牛顿力学得到了最好的证明。
五、发现未知天体
海王星发现之后,人们发现它的轨道也与理论计算的不一致。于是几位学者用亚当斯和勒维耶的方法预言另一颗新行星的存在.
在预言提出之后,1930年,汤博发现了太阳系的后来曾被称为第九大行星的冥王星。
五、发现未知天体
海王星、冥王星的发现最终确立了万有引力定律的地位,也成为科学史上的美谈。诺贝尔物理学奖获得者,物理学家冯·劳厄说:
“没有任何东西向牛顿引力理论对行星轨道的计算那样,如此有力地树起人们对年轻的物理学的尊敬。从此以后,这门自然科学成了巨大的精神王国…… ”
