沪教版数学六年级第二学期7.2角 练习试题(word版、含答案)
文档属性
| 名称 | 沪教版数学六年级第二学期7.2角 练习试题(word版、含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 57.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-25 00:00:00 | ||
图片预览

文档简介
7.2角
(限时60分钟 满分120分)
一、选择(本题共计7小题,每题5分,共计35分)
1.如图,下列表示角的方法,错误的是( )
A.∠1与∠AOB表示同一个角
B.∠AOC也可用∠O来表示
C.图中共有三个角:∠AOB、∠AOC、∠BOC
D.∠β表示的是∠BOC
2.如果 和 互余,则下列式子中表示 补角是( )
①180°- ;② +2 ;③2 + ;④ +90°
A.①②④ B.①②③ C.①③④ D.②③④
3.下列关于角的说法正确的个数是( )
①角是由两条射线组成的图形;②角的边越长,角越大;③在角一边延长线上取一点D;④角可以看成由一条射线绕着它的端点旋转而形成的图形.
A.1个 B.2个 C.3个 D.4个
4.如图,已知∠1=66°15',则∠2的度数为( )
A.113°45' B.123°45' C.23°45' D.25°45'
5.如图,锐角三角形ABC中,BC>AB>AC,甲、乙两人想找一点P,使得∠BPC与∠A互补,其作法分别如下:
(甲)以A为圆心,AC长为半径画弧交AB于P点,则P即为所求;
(乙)作过B点且与AB垂直的直线l,作过C点且与AC垂直的直线,交l于P点,则P即为所求.
对于甲、乙两人的作法,下列叙述正确的是( )
A.两人皆正确 B.两人皆错误
C.甲正确,乙错误 D.甲错误,乙正确
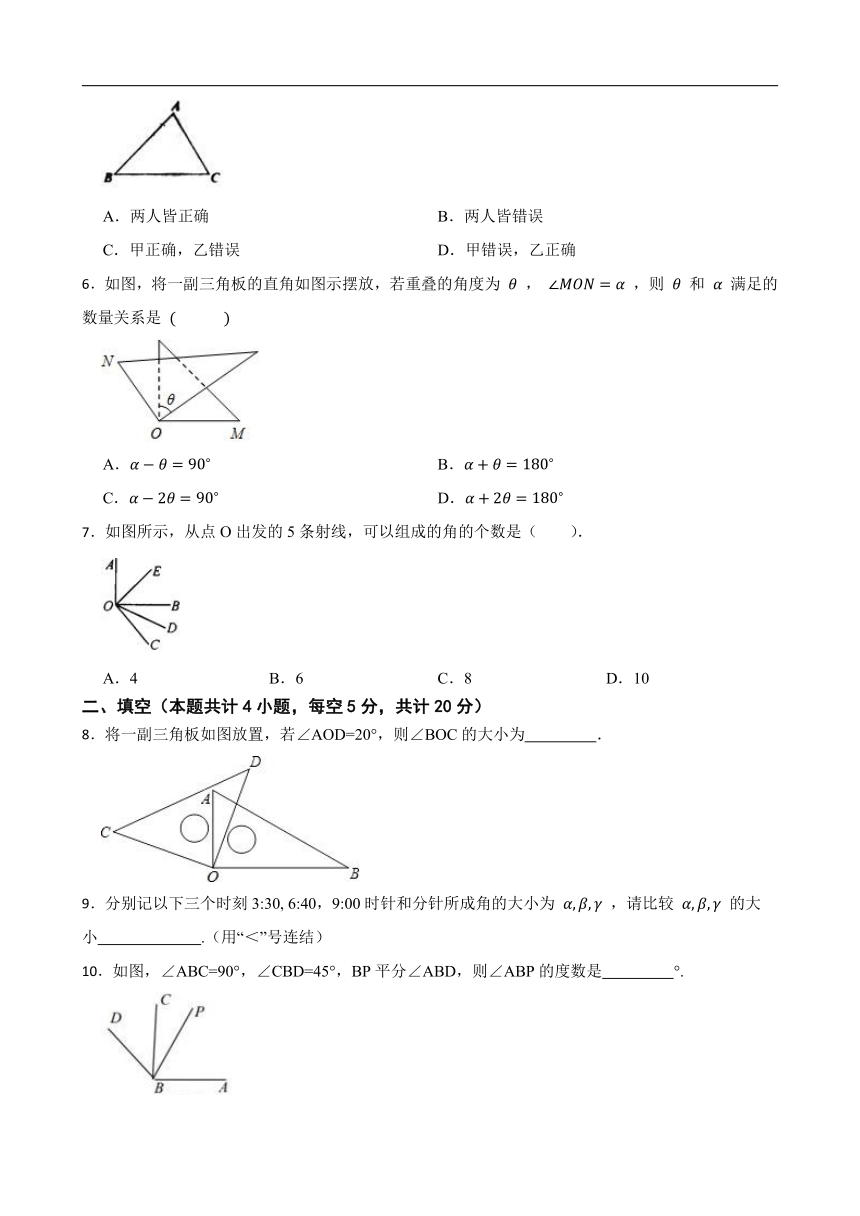
6.如图,将一副三角板的直角如图示摆放,若重叠的角度为 , ,则 和 满足的数量关系是
A. B.
C. D.
7.如图所示,从点O出发的5条射线,可以组成的角的个数是( ).
A.4 B.6 C.8 D.10
二、填空(本题共计4小题,每空5分,共计20分)
8.将一副三角板如图放置,若∠AOD=20°,则∠BOC的大小为 .
9.分别记以下三个时刻3:30, 6:40,9:00时针和分针所成角的大小为 ,请比较 的大小 .(用“<”号连结)
10.如图,∠ABC=90°,∠CBD=45°,BP平分∠ABD,则∠ABP的度数是 °.
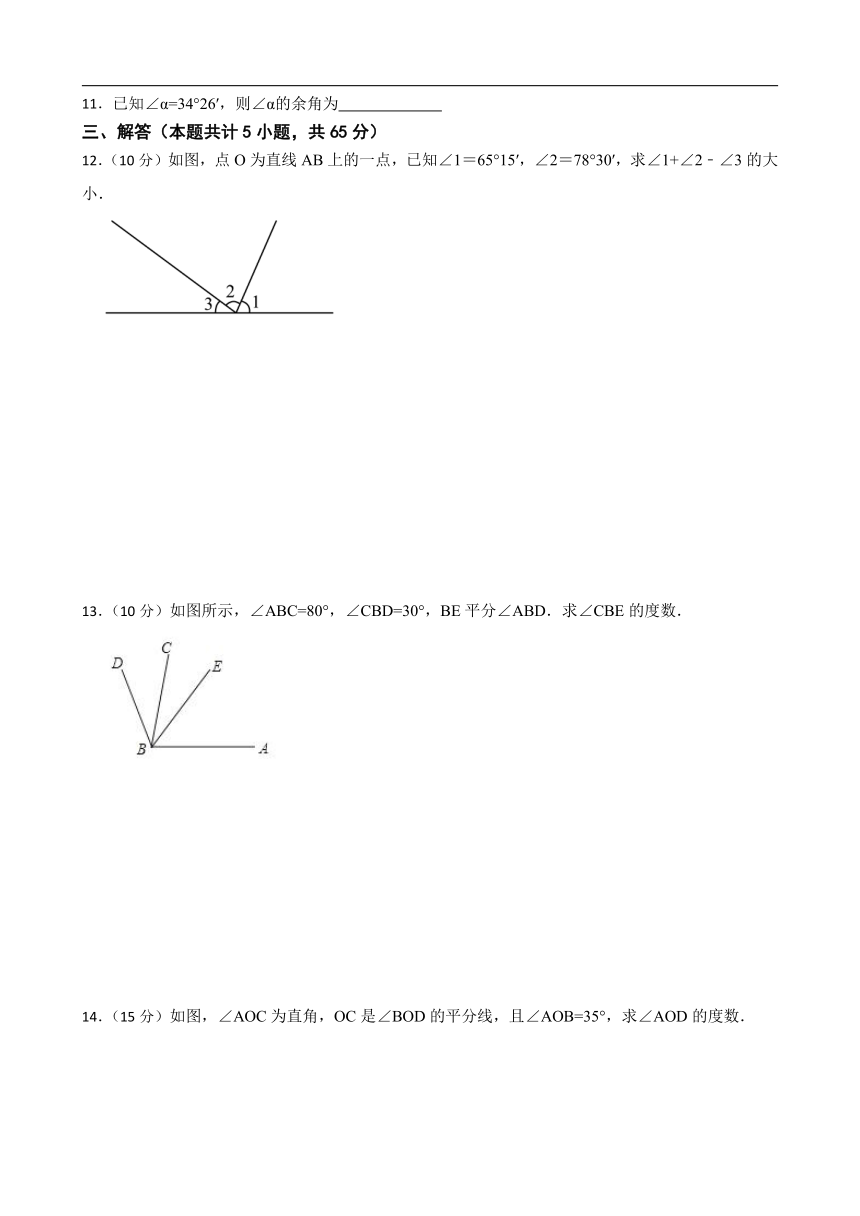
11.已知∠α=34°26′,则∠α的余角为
三、解答(本题共计5小题,共65分)
12.(10分)如图,点O为直线AB上的一点,已知∠1=65°15′,∠2=78°30′,求∠1+∠2﹣∠3的大小.
13.(10分)如图所示,∠ABC=80°,∠CBD=30°,BE平分∠ABD.求∠CBE的度数.
14.(15分)如图,∠AOC为直角,OC是∠BOD的平分线,且∠AOB=35°,求∠AOD的度数.
15.(15分)(1)1点20分时,时钟的时针与分针的夹角是几度?
(2)在时钟上,7点到8点之间,时针和分针何时成30°的角?
16.(15分)如图,O是AB上一点,∠COD=90°,∠AOE= ∠AOC,∠BOD-∠AOE=26°,求∠BOE的度数.
答案部分
1.B
2.A
3.A
4.A
5.D
6.B
7.D
8.160°
9.β<α<γ
10.67.5
11.55°34′
12.解:∵∠1=65°15′,∠2=78°30′,∠1+∠2+∠3=180°,
∠1+∠2=65°15′+78°30′=143°45′,
∴∠3=180°-∠1-∠2=180°-(∠1+∠2)=180°-143°45′=36°15′,
∴∠1+∠2﹣∠3=143°45′-36°15′=107°30′.
13.解:∠ABD=∠ABC+∠CBD=80°+30°=110°;
∵BE是∠ABD的平分线,
∴∠EBD=∠ABD=55°,
∴∠CBE=∠EBD﹣∠CBD=55°﹣30°=25°.
14.解:∵∠BOC=AOC﹣∠AOB=90°﹣35°=55°,又OC平分∠BOD,
∴∠COD=∠BOC=55°,
∴∠AOD=∠AOC+∠COD=90°+55°=145°.
15.(1)解:1点20分,分针与时针的夹角为120°-30°-0.5°×20=80°
(2)解:分针的转动速度为:6°/分,时针的转动速度为:0.5°/分,
①原来时针与分针的夹角为210°,设x分钟时,第一次夹角为30°
可得:6x-0.5x=210-30,
解得
②原来时针与分针的夹角为210°,设x分钟时,第二次夹角为30°
可得:6x-0.5x=210+30,
解得:
即当7点 分或7点 分时,时针和分针成30°的角。
16.解:∵∠COD=90°
∴∠AOC+∠BOD=90°
∵∠AOE= ∠AOC即∠AOC=3∠AOE
∴3∠AOE+∠BOD=90°
∵∠BOD-∠AOE=26°即∠BOD=26°+∠AOE
∴3∠AOE+26°+∠AOE=90°
∴∠AOE=16°
∴∠BOE=180°-∠AOE=180°-16°=164°
答:∠BOE的度数为164°.
(限时60分钟 满分120分)
一、选择(本题共计7小题,每题5分,共计35分)
1.如图,下列表示角的方法,错误的是( )
A.∠1与∠AOB表示同一个角
B.∠AOC也可用∠O来表示
C.图中共有三个角:∠AOB、∠AOC、∠BOC
D.∠β表示的是∠BOC
2.如果 和 互余,则下列式子中表示 补角是( )
①180°- ;② +2 ;③2 + ;④ +90°
A.①②④ B.①②③ C.①③④ D.②③④
3.下列关于角的说法正确的个数是( )
①角是由两条射线组成的图形;②角的边越长,角越大;③在角一边延长线上取一点D;④角可以看成由一条射线绕着它的端点旋转而形成的图形.
A.1个 B.2个 C.3个 D.4个
4.如图,已知∠1=66°15',则∠2的度数为( )
A.113°45' B.123°45' C.23°45' D.25°45'
5.如图,锐角三角形ABC中,BC>AB>AC,甲、乙两人想找一点P,使得∠BPC与∠A互补,其作法分别如下:
(甲)以A为圆心,AC长为半径画弧交AB于P点,则P即为所求;
(乙)作过B点且与AB垂直的直线l,作过C点且与AC垂直的直线,交l于P点,则P即为所求.
对于甲、乙两人的作法,下列叙述正确的是( )
A.两人皆正确 B.两人皆错误
C.甲正确,乙错误 D.甲错误,乙正确
6.如图,将一副三角板的直角如图示摆放,若重叠的角度为 , ,则 和 满足的数量关系是
A. B.
C. D.
7.如图所示,从点O出发的5条射线,可以组成的角的个数是( ).
A.4 B.6 C.8 D.10
二、填空(本题共计4小题,每空5分,共计20分)
8.将一副三角板如图放置,若∠AOD=20°,则∠BOC的大小为 .
9.分别记以下三个时刻3:30, 6:40,9:00时针和分针所成角的大小为 ,请比较 的大小 .(用“<”号连结)
10.如图,∠ABC=90°,∠CBD=45°,BP平分∠ABD,则∠ABP的度数是 °.
11.已知∠α=34°26′,则∠α的余角为
三、解答(本题共计5小题,共65分)
12.(10分)如图,点O为直线AB上的一点,已知∠1=65°15′,∠2=78°30′,求∠1+∠2﹣∠3的大小.
13.(10分)如图所示,∠ABC=80°,∠CBD=30°,BE平分∠ABD.求∠CBE的度数.
14.(15分)如图,∠AOC为直角,OC是∠BOD的平分线,且∠AOB=35°,求∠AOD的度数.
15.(15分)(1)1点20分时,时钟的时针与分针的夹角是几度?
(2)在时钟上,7点到8点之间,时针和分针何时成30°的角?
16.(15分)如图,O是AB上一点,∠COD=90°,∠AOE= ∠AOC,∠BOD-∠AOE=26°,求∠BOE的度数.
答案部分
1.B
2.A
3.A
4.A
5.D
6.B
7.D
8.160°
9.β<α<γ
10.67.5
11.55°34′
12.解:∵∠1=65°15′,∠2=78°30′,∠1+∠2+∠3=180°,
∠1+∠2=65°15′+78°30′=143°45′,
∴∠3=180°-∠1-∠2=180°-(∠1+∠2)=180°-143°45′=36°15′,
∴∠1+∠2﹣∠3=143°45′-36°15′=107°30′.
13.解:∠ABD=∠ABC+∠CBD=80°+30°=110°;
∵BE是∠ABD的平分线,
∴∠EBD=∠ABD=55°,
∴∠CBE=∠EBD﹣∠CBD=55°﹣30°=25°.
14.解:∵∠BOC=AOC﹣∠AOB=90°﹣35°=55°,又OC平分∠BOD,
∴∠COD=∠BOC=55°,
∴∠AOD=∠AOC+∠COD=90°+55°=145°.
15.(1)解:1点20分,分针与时针的夹角为120°-30°-0.5°×20=80°
(2)解:分针的转动速度为:6°/分,时针的转动速度为:0.5°/分,
①原来时针与分针的夹角为210°,设x分钟时,第一次夹角为30°
可得:6x-0.5x=210-30,
解得
②原来时针与分针的夹角为210°,设x分钟时,第二次夹角为30°
可得:6x-0.5x=210+30,
解得:
即当7点 分或7点 分时,时针和分针成30°的角。
16.解:∵∠COD=90°
∴∠AOC+∠BOD=90°
∵∠AOE= ∠AOC即∠AOC=3∠AOE
∴3∠AOE+∠BOD=90°
∵∠BOD-∠AOE=26°即∠BOD=26°+∠AOE
∴3∠AOE+26°+∠AOE=90°
∴∠AOE=16°
∴∠BOE=180°-∠AOE=180°-16°=164°
答:∠BOE的度数为164°.
