《2.5实数（第1课时）》教案

教学目标：
知道无理数是客观存在的，了解无理数和实数的概念，能对实数按要求进行分类，同时会判断一个数是有理数还是无理数。
知道实数和数轴上的点一一对应。
二、教学重难点：
重点：会判断一个数是有理数还是无理数。
难点：不是有理数，有多大？
教学过程：
【新知预习】
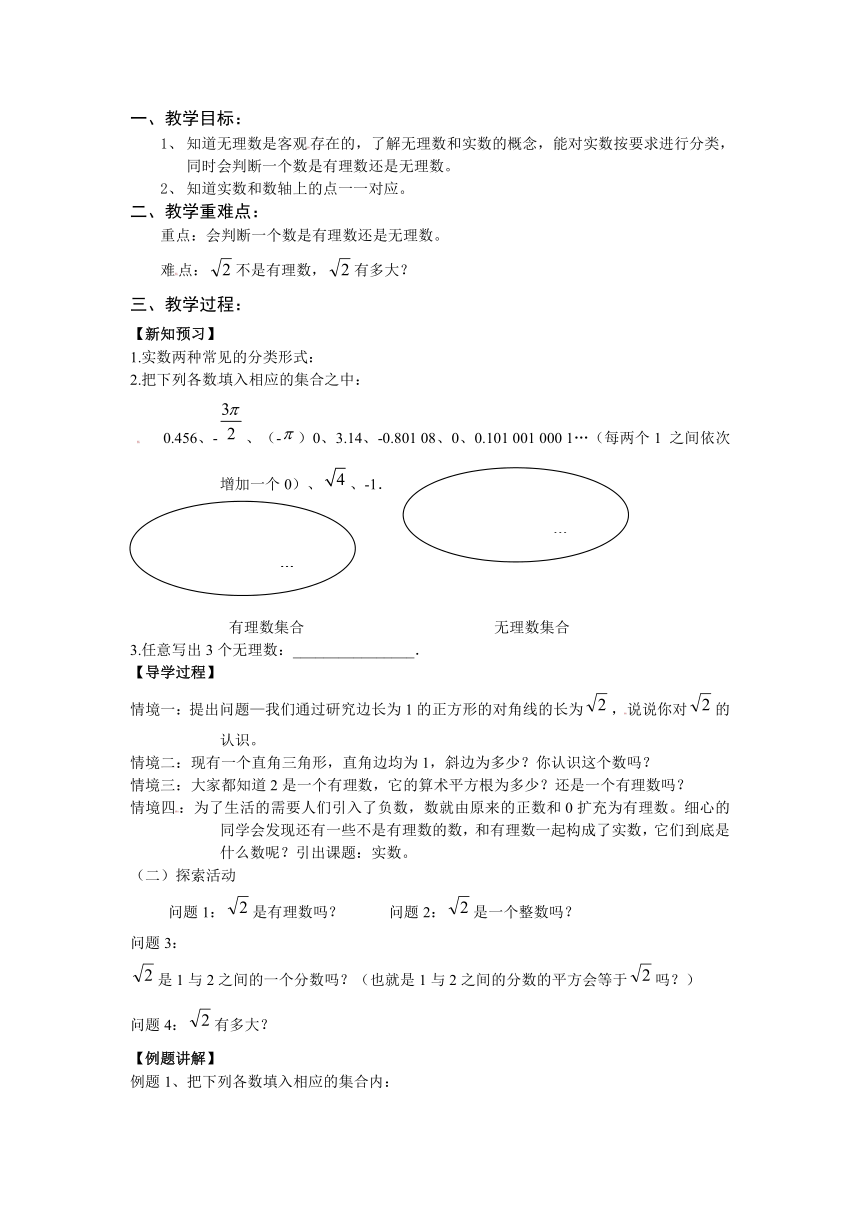
1.实数两种常见的分类形式：
2.把下列各数填入相应的集合之中：
0.456、-、（-）0、3.14、-0.801 08、0、0.101 001 000 1…（每两个1之间依次增加一个0）、、-1．
有理数集合 无理数集合
3.任意写出3个无理数：________________．
【导学过程】
情境一：提出问题—我们通过研究边长为1的正方形的对角线的长为，说说你对的认识。
情境二：现有一个直角三角形，直角边均为1，斜边为多少？你认识这个数吗？
情境三：大家都知道2是一个有理数，它的算术平方根为多少？还是一个有理数吗？
情境四：为了生活的需要人们引入了负数，数就由原来的正数和0扩充为有理数。细心的同学会发现还有一些不是有理数的数，和有理数一起构成了实数，它们到底是什么数呢？引出课题：实数。
（二）探索活动
问题1：是有理数吗？ 问题2：是一个整数吗？
问题3：
是1与2之间的一个分数吗？（也就是1与2之间的分数的平方会等于吗？）
问题4：有多大？
【例题讲解】
例题1、把下列各数填入相应的集合内：
、、0、、、、3.14159、-0.020020002 0.12121121112…
(1)有理数集合{ }
(2)无理数集合{ }
(3)正实数集合{ }
(4)负实数集合{ }
分析：要正确地将以上各数分类，就必须对各类书的概念十分清晰，用概念来判定。
【反馈练习】
1.判断正误，若不对，请说明理由，并加以改正。
（1）无理数都是无限小数。 （2）带根号的数不一定是无理数。
（3）无限小数都是无理数。 （4）数轴上的点表示有理数。
（5）不带根号的数一定是有理数。
2. ．数、、中，无理数有（ ）。
（A）0个 （B）1个 （C）2个 （D）3个
3.（1）把下列各数填入相应的集合内：-7，0.32，， ，，- 。
有理数集合：{ …}；无理数集合：{ …}；
无理数集合：{ …}．
【课后作业】 补充习题2.5实数
教学反思