沪科版数学七年级下册 8.2 整式乘法---多项式与多项式相乘 课件 (共14张PPT)
文档属性
| 名称 | 沪科版数学七年级下册 8.2 整式乘法---多项式与多项式相乘 课件 (共14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-26 07:32:30 | ||
图片预览





文档简介
(共14张PPT)
8.2 整式乘法
多项式与多项式相乘
教学目标
2、会用树形图进行多项式乘
以多项式的运算。
1、理解多项式与多项式的乘
法法则 。
知识回顾
单项式与多项式乘法法则:
单项式与多项式相乘,用单项式和多项式的每一项分别相乘,再把所得的积相加.
计算:
-3x2
=-3x2·x2=-3x4
=-3x2·(-1)=3x2
x2
-1
.
.
3x2
=3x2·x2=3x4
=3x2·1=3x2
x2
1
.
.
解:=-3x4+3x2+3x4+3x2
=(-3x4+3x4)+(3x2+3x2)
=6x2
-3x2(x2-1)+(x2+1)3x2
探究新知
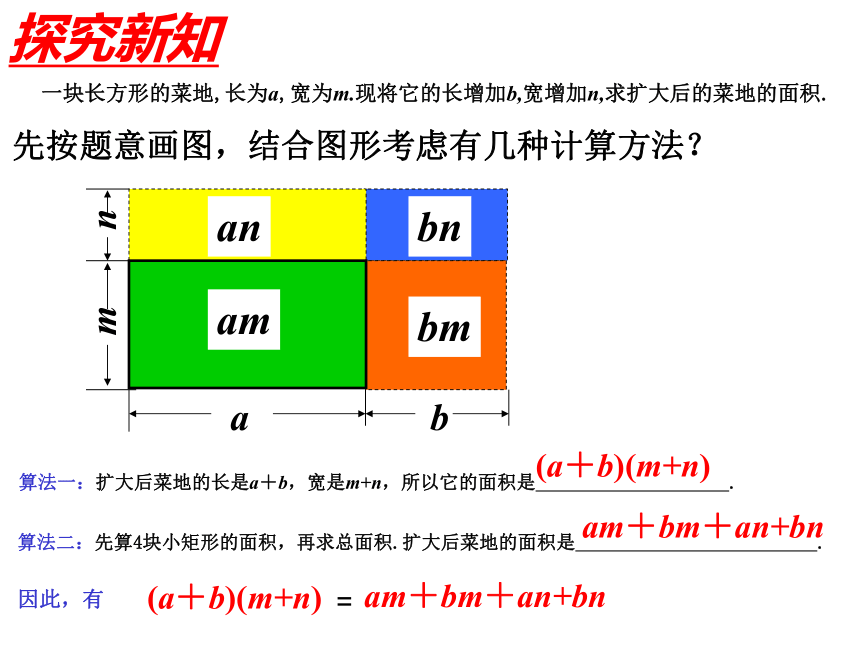
先按题意画图,结合图形考虑有几种计算方法?
b
n
m
a
算法一:扩大后菜地的长是a+b,宽是m+n,所以它的面积是 .
算法二:先算4块小矩形的面积,再求总面积.扩大后菜地的面积是 .
因此,有
(a+b)(m+n)
am+bm+an+bn
=
(a+b)(m+n)
am+bm+an+bn
am
bn
an
bm
一块长方形的菜地,长为a,宽为m.现将它的长增加b,宽增加n,求扩大后的菜地的面积.
(a+b) (m+n) =
a
=a·m=am
=a·n=an
m
n
.
.
b
=b·m=bm
=b·n=bn
m
n
.
.
am + an+ bm+ bn
多项式与多项式的乘法法则:
多项式与多项式相乘,先用一个多项式的每一项与另一个多项式的每一项相乘,再把所得的积相加.
(a+b) (m+n) =
am
+ an
+ bm
+ bn
-2x
=-2x·3x=-6x2
=-2x·(-2)=4x
3x
-2
.
.
-1
=-1·3x=-3x
=-1·(-2)=2
3x
-2
.
.
解:=-6x2+4x-3x+2
=-6x2+x+2
草稿:
ax
=ax·cx=acx2
=ax·d=adx
cx
d
.
.
b
=b·cx=bcx
=b·d=bd
cx
d
.
.
解:=acx2+adx+bcx+bd
=acx2+(adx+bcx)+bd
草稿:
=acx2+(ad+bc)x+bd
1.计算:
2n
=2n·n=2n2
=2n·(-3)=-6n
n
-3
.
.
6
=6·n=6n
=6·(-3)=-18
n
-3
.
.
草稿:
3x
=3x·3x=9x2
=3x·y=3xy
3x
y
.
.
-y
=-y·3x=-3xy
=-y·y=-y2
3x
y
.
.
草稿:
解:=2n2-6n+6n-18
=2n2-18
解:=9x2+3xy-3xy-y2
=9x2-y2
a
=a·a2=a3
=a·b2=ab2
解:=a3-a2b+ab2+a2b-ab2+b3
草稿:
草稿:
a2
b2
.
.
-ab
=a·(-ab)=-a2b
b
=b·a2=a2b
=b·b2=b3
a2
b2
.
.
-ab
=b·(-ab)=-ab2
=a3+(-a2b+a2b)+(ab2-ab2)+b3
=a3+b3
y
=y·y2=y3
=y·1=y
解:=y3+y2+y+2y2+2y+2
y2
1
.
.
y
=y·y=y2
2
=2·y2=2y2
=2*1=2
y2
1
.
.
y
=2·y=2y
=y3+(y2+2y2)+(y+2y)+2
=y3+3y2+3y+2
2.计算:
3.计算:
解:=x3+x2y+xy2-x2y-xy2-y3
=x3+(x2y-x2y) +(xy2-xy2)-y3
=x3+y3
解:=3a2-3a-2a+2+a2+2a+a+2
=(3a2+a2)+(-3a-2a+2a+a)+(2+2)
=4a2-2a+4
4.计算:
提高题
5x2-(x-2)(3x+1)-2(x+1)(x-5)
5.计算:
若(x-1)(x+2)=x2+mx+n求m+n的值。
6.计算:
如果(x+m)(x-8)的积中不含x的一次项,
那么m的值是多少?
填空:
5 6
1 (-6)
(-1) (-6)
(-5) 6
观察上面四个等式,你能发现什么规律?
拓展学习
课堂小结
1.多项式与多项式相乘的法则:
先用一个多项式的每一项与另一个多项式的每一项相乘 ;
再把所得的积相加.
(a+b) (m+n) =
am
+ bm
+ an
+ bn
(a+b) (m+n) =
a
=a·m=am
=a·n=an
m
n
.
.
b
=b·m=bm
=b·n=bn
m
n
.
.
am + an+ bm+ bn
课后作业
一、必做:课本66页2、(2),3、(2)题
二、选做:
小东找来一张挂历画包数学课本,已知课本长a厘米,宽b厘米,厚c厘米,小东想将课本封面与封底的每一边都包进去m厘米.问小东应在挂历画上裁下一块多大面积的长方形?
8.2 整式乘法
多项式与多项式相乘
教学目标
2、会用树形图进行多项式乘
以多项式的运算。
1、理解多项式与多项式的乘
法法则 。
知识回顾
单项式与多项式乘法法则:
单项式与多项式相乘,用单项式和多项式的每一项分别相乘,再把所得的积相加.
计算:
-3x2
=-3x2·x2=-3x4
=-3x2·(-1)=3x2
x2
-1
.
.
3x2
=3x2·x2=3x4
=3x2·1=3x2
x2
1
.
.
解:=-3x4+3x2+3x4+3x2
=(-3x4+3x4)+(3x2+3x2)
=6x2
-3x2(x2-1)+(x2+1)3x2
探究新知
先按题意画图,结合图形考虑有几种计算方法?
b
n
m
a
算法一:扩大后菜地的长是a+b,宽是m+n,所以它的面积是 .
算法二:先算4块小矩形的面积,再求总面积.扩大后菜地的面积是 .
因此,有
(a+b)(m+n)
am+bm+an+bn
=
(a+b)(m+n)
am+bm+an+bn
am
bn
an
bm
一块长方形的菜地,长为a,宽为m.现将它的长增加b,宽增加n,求扩大后的菜地的面积.
(a+b) (m+n) =
a
=a·m=am
=a·n=an
m
n
.
.
b
=b·m=bm
=b·n=bn
m
n
.
.
am + an+ bm+ bn
多项式与多项式的乘法法则:
多项式与多项式相乘,先用一个多项式的每一项与另一个多项式的每一项相乘,再把所得的积相加.
(a+b) (m+n) =
am
+ an
+ bm
+ bn
-2x
=-2x·3x=-6x2
=-2x·(-2)=4x
3x
-2
.
.
-1
=-1·3x=-3x
=-1·(-2)=2
3x
-2
.
.
解:=-6x2+4x-3x+2
=-6x2+x+2
草稿:
ax
=ax·cx=acx2
=ax·d=adx
cx
d
.
.
b
=b·cx=bcx
=b·d=bd
cx
d
.
.
解:=acx2+adx+bcx+bd
=acx2+(adx+bcx)+bd
草稿:
=acx2+(ad+bc)x+bd
1.计算:
2n
=2n·n=2n2
=2n·(-3)=-6n
n
-3
.
.
6
=6·n=6n
=6·(-3)=-18
n
-3
.
.
草稿:
3x
=3x·3x=9x2
=3x·y=3xy
3x
y
.
.
-y
=-y·3x=-3xy
=-y·y=-y2
3x
y
.
.
草稿:
解:=2n2-6n+6n-18
=2n2-18
解:=9x2+3xy-3xy-y2
=9x2-y2
a
=a·a2=a3
=a·b2=ab2
解:=a3-a2b+ab2+a2b-ab2+b3
草稿:
草稿:
a2
b2
.
.
-ab
=a·(-ab)=-a2b
b
=b·a2=a2b
=b·b2=b3
a2
b2
.
.
-ab
=b·(-ab)=-ab2
=a3+(-a2b+a2b)+(ab2-ab2)+b3
=a3+b3
y
=y·y2=y3
=y·1=y
解:=y3+y2+y+2y2+2y+2
y2
1
.
.
y
=y·y=y2
2
=2·y2=2y2
=2*1=2
y2
1
.
.
y
=2·y=2y
=y3+(y2+2y2)+(y+2y)+2
=y3+3y2+3y+2
2.计算:
3.计算:
解:=x3+x2y+xy2-x2y-xy2-y3
=x3+(x2y-x2y) +(xy2-xy2)-y3
=x3+y3
解:=3a2-3a-2a+2+a2+2a+a+2
=(3a2+a2)+(-3a-2a+2a+a)+(2+2)
=4a2-2a+4
4.计算:
提高题
5x2-(x-2)(3x+1)-2(x+1)(x-5)
5.计算:
若(x-1)(x+2)=x2+mx+n求m+n的值。
6.计算:
如果(x+m)(x-8)的积中不含x的一次项,
那么m的值是多少?
填空:
5 6
1 (-6)
(-1) (-6)
(-5) 6
观察上面四个等式,你能发现什么规律?
拓展学习
课堂小结
1.多项式与多项式相乘的法则:
先用一个多项式的每一项与另一个多项式的每一项相乘 ;
再把所得的积相加.
(a+b) (m+n) =
am
+ bm
+ an
+ bn
(a+b) (m+n) =
a
=a·m=am
=a·n=an
m
n
.
.
b
=b·m=bm
=b·n=bn
m
n
.
.
am + an+ bm+ bn
课后作业
一、必做:课本66页2、(2),3、(2)题
二、选做:
小东找来一张挂历画包数学课本,已知课本长a厘米,宽b厘米,厚c厘米,小东想将课本封面与封底的每一边都包进去m厘米.问小东应在挂历画上裁下一块多大面积的长方形?
