沪科版数学七年级下册 7.1 不等式及其基本性质 课件 (共25张PPT)
文档属性
| 名称 | 沪科版数学七年级下册 7.1 不等式及其基本性质 课件 (共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 720.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-26 07:34:22 | ||
图片预览







文档简介
(共25张PPT)
7.1 不等式及其基本性质
中考考点清单
考点1
等式的性质
1.如果a=b,那么a±c=①_______
2.如果a=b,那么ac=②______
3.如果a=b, c≠0那么 ③_____
b±c
bc
第一节 一次方程(组)
考点2
一元一次方程及其解法
1. 一元一次方程
(1)满足的条件:a.只含有④_____未知数;
b.未知数的最高次数是⑤_____;
c.等号的两边都是整式.
(2)一般形式:ax+b=0(a≠0)
(3)解:x= (a≠0)
1
一个
2.解一元一次方程的方法及步骤
(1)方法
利用等式的性质,把方程变形成“x=a(a为已知数)”的形式;
(2)步骤
步骤 注意事项
去分母 不要漏乘不含分母的项(尤其是整数项)
去括号 括号前是负号时,去括号后括号内各项均要变号
移项 被移项要改变符号
合并同类项 系数相加,字母及其指数均不变
系数化为1 解的分子、分母位置不要颠倒
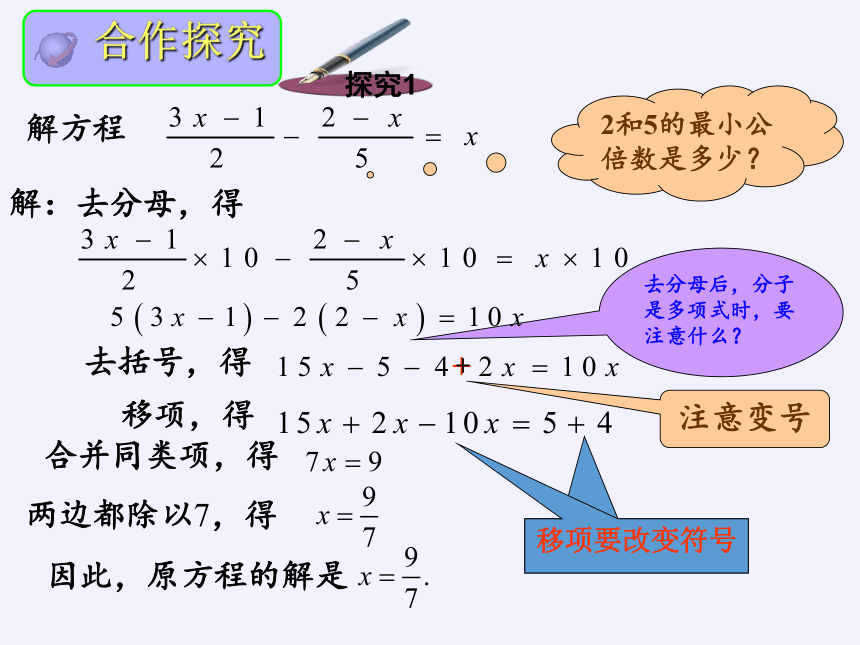
去分母后,分子是多项式时,要注意什么?
注意变号
解:去分母,得
2和5的最小公倍数是多少?
+
去括号,得
移项,得
合并同类项,得
两边都除以7,得
因此,原方程的解是
解方程
移项要改变符号
合作探究
探究1
二元一次方程(组)及其解法
考点3
二元一次方程:含有两个未知数(x和y),并且含有
未知数的项的次数都是1的整式方程.
2. 二元一次方程组:方程组中有两个未知数,每个未知
数的项的次数都是1,并且一共有两个方程.
3. 二元一次方程的解:使二元一次方程两边的值相等的两个未知数的值.
4.二元一次方程组的解:二元一次方程组的两个方程的公共解.
5.解二元一次方程组的基本思想:⑥____,将二元一次方程组转化为⑦_________方程,然后求解.
一元一次
消元
6. 二元一次方程组的解法
(1)代入消元法
a.变——用含有一个未知数的代数式表示另一个未知数
b.代——消去一个元
c.解——分别求出两个未知数的值
d.写——写出方程组的解
(2)加减消元法
a.变——同一个未知数的系数相同或互为相反数
b.加减——消去一个元
c.解——分别求出两个未知数的值
d.写——写出方程组的解
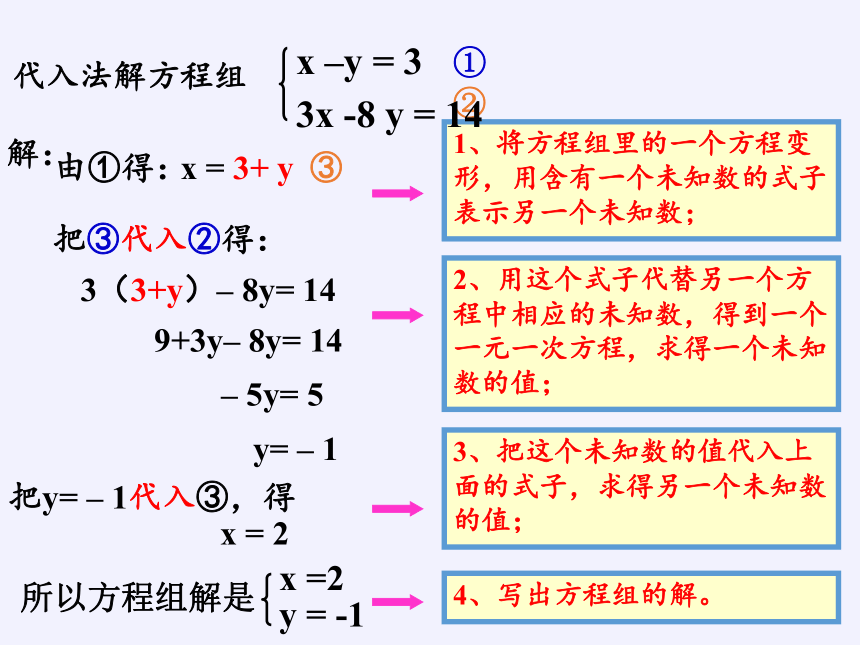
代入法解方程组
解:
①
②
由①得:
x = 3+ y
③
把③代入②得:
3(3+y)– 8y= 14
把y= – 1代入③,得
x = 2
1、将方程组里的一个方程变形,用含有一个未知数的式子表示另一个未知数;
2、用这个式子代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值;
3、把这个未知数的值代入上面的式子,求得另一个未知数的值;
4、写出方程组的解。
x –y = 3
3x -8 y = 14
9+3y– 8y= 14
– 5y= 5
y= – 1
所以方程组解是
x =2
y = -1
例2
如何解方程组
解:①-②,得 8y = -8 ,(依据什么 )
解得 y = -1 .
把y=-1 代入①,得 2x + 5×(-1) = 9 ,
解得 x = 7 .
∴原方程组的一个解是
2x+5y=9
2x-3y=17
①
②
x = 7
y = -1
例题解答
例3、解方程组
解:①+②,得 9x = 9 ,
解得 x = 1 .
把x=1 代入①,得 7×1+3y = 1 ,
解得 y = -2 .
∴原方程组的一个解是
7x+3y=1
2x-3y=8
①
②
x = 1
y = -2
例题解答
例4、解方程组
解:①×4,得 12x+16y = 32 ③
②×3,得 12x+9y = -3 ④
③-④,得 7y = 35
解得 y = 5
把y = 5代入①, 得 3x+4×5=8
解得 x = -4
∴原方程组的一个解是
3x+4y=8
4x+3y=-1
①
②
x = -4
y = 5
本 课 小 结
②步骤及解法
3、 二元一次方程(组)的解法及步骤
4、数学思想:整体思想、消元思想
1、等式的基本性质
①定义
2、一元一次方程(组)的:
布置作业:
1、综合练习册37--38页
2、预习一元二次方程及其解法
再见
考点1
一元二次方程及其解法
1. 一元二次方程:只含有一个未知数(一元),并且未知数的最高次数是2(二次)的整式方程.
2. 一般形式
第二节 一元二次方程
3. 一元二次方程必须具备三个条件:(1)必须是①______方程;
(2)必须只含有②____未知数;
(3)所含未知数的最高次数是③___.
2
整式
1个
【温馨提示】在一元二次方程的一般形式中要注意a≠0.
因为当a=0时,不含有二次项,即不是一元二次方程.
5. 一元二次方程的解法
解法 适用形式 方程的根
直接开 平方法 x2=p(p≥0) x=
( x+n)2=p(p≥0且n ≠0) x=④___________
配方法 可配方为a(x+h)2=k(a≠0且 ≥0) x=
公式法 ax2+bx+c=0 (a≠0,b2-4ac≥0) x=⑤__________
因式分解法 可化为 a(x+m)(x+n)=0 的方程 x=-m, -n
4. 一元二次方程的解
使方程左右两边相等的未知数的值就是这个一元二次方程的解,一元二次方程的解也叫做一元二次方程的根.
口诀:1.方程没有一次项(即b=0),直接开方最理想;如果缺少常数项(即c=0),因式分解没商量;b,c相等都为0,等根是0不要忘;b,c同时不为0,因式分解或配方,也可直接套公式,因题而异择良方;
2.使用配方法较简单的方程特点:将二次项系数化为1后,一次项系数为偶数.
解一元二次方程“丢根”现象
方程x(x-1)=2(x-1)2的根为( )
A.1 B.2 C.1和2 D.1和-2
【解析】方程两边同时除以公因式(x-1)得:
x=2(x-1), … … … … … … … … … … …第一步
移项得:x-2(x-1)=0, … … … … … …第二步
去括号得:x-2x+2=0, … … … … … … …第三步
解得:x=2. … … … … … … … … … …第四步 【答案】B
上述解析过程是从第____步开始出现错误的,应该改为________________,此题最终的结果是___.
C
一
x(x-1)-2(x-1)2=0
【提醒】对于左右两边含有相同因式的一元二次方程,应将方程化为一般式后再求解(或将方程变为等号一边为0,另一边含未知数的式子,利用因式分解法求解),切勿直接约去公因式而丢根.
失
分
点
考点2
一元二次方程根的判别式及根与系数的关系
根的判别式:
一般地,式子b2-4ac叫做一元二次方程ax2+bx+c=0(a≠0)根的判别式,通常用希腊字母“Δ”表示,即Δ=b2-4ac.
2. 一元二次方程根的情况与判别式的关系:
(1) b2-4ac>0 方程有⑥_____________的实数根
(2) b2-4ac=0 方程有⑦__________的实数根
(3) b2-4ac<0 方程⑧_______实数根
没有
两个相等
两个不相等
失
分
点
忽略一元二次方程的二次项系数不为0的条件
关于x的一元二次方程(a-1)x2-2x+1=0有实数根,则a满足( ) A. a≤2 B. a<2且a≠1 C. a≤2且a≠1 D. a≠1
【解析】∵关于x的方程(a-1)x2-2x+1=0有实数根,第一步
∴b2-4ac=4-4(a-1)≥0,… … … … … … … … … 第二步
∴a≤2. … … … … … … … … … … … … … …第三步
【答案】A
上述解题过程从第___步开始出错,错误的原因为___________ ___ ,
此题最终结果为____.
【提醒】在使用根的判别方式解决问题时,如果二次项系数中含有字母,要加上二次项系数不为0这个隐含的限制条件.
三
方程为一元二次方程时,a-1≠0
C
3. 一元二次方程根与系数的关系
(1)若一元二次方程ax2+bx+c=0(a≠0,b2-4ac>0)的两实根分别为x1,x2,则x1+x2=⑨_____,x1x2=⑩____.
(2)常用根与系数关系解决以下问题:
①已知方程及方程一根,求另一个根及未知数;
②不解方程求关于根的式子的值,如求x1+x2,x1·x2;
③由给出的两根满足的条件,确定字母的取值范围.
【易错提示】利用根与系数的关系解题的前提是方程的
两根存在,即注意根的判别式b2-4ac≥0.
考点3
一元二次方程应用的常考类型及关系式
1.增长率等量关系:
A.增长率= ×100%;
B.设a为原来量,m为平均增长率,n为增长次数,b为增长后的量,则有a(1+m)n=b;当m为平均下降率,n为下降次数,b为下降后的量时,则有a(1-m)n=b.
2.利润等量关系: A.利润=售价-成本;
B.利润率= ×100%.
3.面积问题常见图形归纳如下:
第一:如图①,矩形ABCD长为a,宽为b,空白部分的宽为x,则阴影部分的面积表示为(a-2x)(b-2x).
第二:如图②,矩形ABCD长为a,宽为b,阴影部分的宽为x,则空白部分的面积为(a-x)(b-x).
第三:如图③,矩形ABCD长为a,宽为b,阴影部分的宽为x,则空白部分的面积为(a-x)(b-x).
谢 谢
7.1 不等式及其基本性质
中考考点清单
考点1
等式的性质
1.如果a=b,那么a±c=①_______
2.如果a=b,那么ac=②______
3.如果a=b, c≠0那么 ③_____
b±c
bc
第一节 一次方程(组)
考点2
一元一次方程及其解法
1. 一元一次方程
(1)满足的条件:a.只含有④_____未知数;
b.未知数的最高次数是⑤_____;
c.等号的两边都是整式.
(2)一般形式:ax+b=0(a≠0)
(3)解:x= (a≠0)
1
一个
2.解一元一次方程的方法及步骤
(1)方法
利用等式的性质,把方程变形成“x=a(a为已知数)”的形式;
(2)步骤
步骤 注意事项
去分母 不要漏乘不含分母的项(尤其是整数项)
去括号 括号前是负号时,去括号后括号内各项均要变号
移项 被移项要改变符号
合并同类项 系数相加,字母及其指数均不变
系数化为1 解的分子、分母位置不要颠倒
去分母后,分子是多项式时,要注意什么?
注意变号
解:去分母,得
2和5的最小公倍数是多少?
+
去括号,得
移项,得
合并同类项,得
两边都除以7,得
因此,原方程的解是
解方程
移项要改变符号
合作探究
探究1
二元一次方程(组)及其解法
考点3
二元一次方程:含有两个未知数(x和y),并且含有
未知数的项的次数都是1的整式方程.
2. 二元一次方程组:方程组中有两个未知数,每个未知
数的项的次数都是1,并且一共有两个方程.
3. 二元一次方程的解:使二元一次方程两边的值相等的两个未知数的值.
4.二元一次方程组的解:二元一次方程组的两个方程的公共解.
5.解二元一次方程组的基本思想:⑥____,将二元一次方程组转化为⑦_________方程,然后求解.
一元一次
消元
6. 二元一次方程组的解法
(1)代入消元法
a.变——用含有一个未知数的代数式表示另一个未知数
b.代——消去一个元
c.解——分别求出两个未知数的值
d.写——写出方程组的解
(2)加减消元法
a.变——同一个未知数的系数相同或互为相反数
b.加减——消去一个元
c.解——分别求出两个未知数的值
d.写——写出方程组的解
代入法解方程组
解:
①
②
由①得:
x = 3+ y
③
把③代入②得:
3(3+y)– 8y= 14
把y= – 1代入③,得
x = 2
1、将方程组里的一个方程变形,用含有一个未知数的式子表示另一个未知数;
2、用这个式子代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值;
3、把这个未知数的值代入上面的式子,求得另一个未知数的值;
4、写出方程组的解。
x –y = 3
3x -8 y = 14
9+3y– 8y= 14
– 5y= 5
y= – 1
所以方程组解是
x =2
y = -1
例2
如何解方程组
解:①-②,得 8y = -8 ,(依据什么 )
解得 y = -1 .
把y=-1 代入①,得 2x + 5×(-1) = 9 ,
解得 x = 7 .
∴原方程组的一个解是
2x+5y=9
2x-3y=17
①
②
x = 7
y = -1
例题解答
例3、解方程组
解:①+②,得 9x = 9 ,
解得 x = 1 .
把x=1 代入①,得 7×1+3y = 1 ,
解得 y = -2 .
∴原方程组的一个解是
7x+3y=1
2x-3y=8
①
②
x = 1
y = -2
例题解答
例4、解方程组
解:①×4,得 12x+16y = 32 ③
②×3,得 12x+9y = -3 ④
③-④,得 7y = 35
解得 y = 5
把y = 5代入①, 得 3x+4×5=8
解得 x = -4
∴原方程组的一个解是
3x+4y=8
4x+3y=-1
①
②
x = -4
y = 5
本 课 小 结
②步骤及解法
3、 二元一次方程(组)的解法及步骤
4、数学思想:整体思想、消元思想
1、等式的基本性质
①定义
2、一元一次方程(组)的:
布置作业:
1、综合练习册37--38页
2、预习一元二次方程及其解法
再见
考点1
一元二次方程及其解法
1. 一元二次方程:只含有一个未知数(一元),并且未知数的最高次数是2(二次)的整式方程.
2. 一般形式
第二节 一元二次方程
3. 一元二次方程必须具备三个条件:(1)必须是①______方程;
(2)必须只含有②____未知数;
(3)所含未知数的最高次数是③___.
2
整式
1个
【温馨提示】在一元二次方程的一般形式中要注意a≠0.
因为当a=0时,不含有二次项,即不是一元二次方程.
5. 一元二次方程的解法
解法 适用形式 方程的根
直接开 平方法 x2=p(p≥0) x=
( x+n)2=p(p≥0且n ≠0) x=④___________
配方法 可配方为a(x+h)2=k(a≠0且 ≥0) x=
公式法 ax2+bx+c=0 (a≠0,b2-4ac≥0) x=⑤__________
因式分解法 可化为 a(x+m)(x+n)=0 的方程 x=-m, -n
4. 一元二次方程的解
使方程左右两边相等的未知数的值就是这个一元二次方程的解,一元二次方程的解也叫做一元二次方程的根.
口诀:1.方程没有一次项(即b=0),直接开方最理想;如果缺少常数项(即c=0),因式分解没商量;b,c相等都为0,等根是0不要忘;b,c同时不为0,因式分解或配方,也可直接套公式,因题而异择良方;
2.使用配方法较简单的方程特点:将二次项系数化为1后,一次项系数为偶数.
解一元二次方程“丢根”现象
方程x(x-1)=2(x-1)2的根为( )
A.1 B.2 C.1和2 D.1和-2
【解析】方程两边同时除以公因式(x-1)得:
x=2(x-1), … … … … … … … … … … …第一步
移项得:x-2(x-1)=0, … … … … … …第二步
去括号得:x-2x+2=0, … … … … … … …第三步
解得:x=2. … … … … … … … … … …第四步 【答案】B
上述解析过程是从第____步开始出现错误的,应该改为________________,此题最终的结果是___.
C
一
x(x-1)-2(x-1)2=0
【提醒】对于左右两边含有相同因式的一元二次方程,应将方程化为一般式后再求解(或将方程变为等号一边为0,另一边含未知数的式子,利用因式分解法求解),切勿直接约去公因式而丢根.
失
分
点
考点2
一元二次方程根的判别式及根与系数的关系
根的判别式:
一般地,式子b2-4ac叫做一元二次方程ax2+bx+c=0(a≠0)根的判别式,通常用希腊字母“Δ”表示,即Δ=b2-4ac.
2. 一元二次方程根的情况与判别式的关系:
(1) b2-4ac>0 方程有⑥_____________的实数根
(2) b2-4ac=0 方程有⑦__________的实数根
(3) b2-4ac<0 方程⑧_______实数根
没有
两个相等
两个不相等
失
分
点
忽略一元二次方程的二次项系数不为0的条件
关于x的一元二次方程(a-1)x2-2x+1=0有实数根,则a满足( ) A. a≤2 B. a<2且a≠1 C. a≤2且a≠1 D. a≠1
【解析】∵关于x的方程(a-1)x2-2x+1=0有实数根,第一步
∴b2-4ac=4-4(a-1)≥0,… … … … … … … … … 第二步
∴a≤2. … … … … … … … … … … … … … …第三步
【答案】A
上述解题过程从第___步开始出错,错误的原因为___________ ___ ,
此题最终结果为____.
【提醒】在使用根的判别方式解决问题时,如果二次项系数中含有字母,要加上二次项系数不为0这个隐含的限制条件.
三
方程为一元二次方程时,a-1≠0
C
3. 一元二次方程根与系数的关系
(1)若一元二次方程ax2+bx+c=0(a≠0,b2-4ac>0)的两实根分别为x1,x2,则x1+x2=⑨_____,x1x2=⑩____.
(2)常用根与系数关系解决以下问题:
①已知方程及方程一根,求另一个根及未知数;
②不解方程求关于根的式子的值,如求x1+x2,x1·x2;
③由给出的两根满足的条件,确定字母的取值范围.
【易错提示】利用根与系数的关系解题的前提是方程的
两根存在,即注意根的判别式b2-4ac≥0.
考点3
一元二次方程应用的常考类型及关系式
1.增长率等量关系:
A.增长率= ×100%;
B.设a为原来量,m为平均增长率,n为增长次数,b为增长后的量,则有a(1+m)n=b;当m为平均下降率,n为下降次数,b为下降后的量时,则有a(1-m)n=b.
2.利润等量关系: A.利润=售价-成本;
B.利润率= ×100%.
3.面积问题常见图形归纳如下:
第一:如图①,矩形ABCD长为a,宽为b,空白部分的宽为x,则阴影部分的面积表示为(a-2x)(b-2x).
第二:如图②,矩形ABCD长为a,宽为b,阴影部分的宽为x,则空白部分的面积为(a-x)(b-x).
第三:如图③,矩形ABCD长为a,宽为b,阴影部分的宽为x,则空白部分的面积为(a-x)(b-x).
谢 谢
