实际问题与二元一次方程组
文档属性
| 名称 | 实际问题与二元一次方程组 |  | |
| 格式 | zip | ||
| 文件大小 | 498.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-08 19:39:36 | ||
图片预览








文档简介
课件27张PPT。8.3 实际问题与二元一次方程组
悟空顺风探妖踪,
千里只行四分钟.
归时四分行六百,
风速多少才称雄?顺风速度=悟空飞行速度+风速
逆风速度=悟空飞行速度-风速
解:设悟空飞行速度是每分钟x里, 风速是每分钟y里,4(x-y)=600 x=200 y=50答:风速是每分钟50里.4(x+y)=1000 解得:依题意得
养牛场原有30只大牛和15只小牛,1天约需要饲料675kg;一周后又购进12只大牛和5只小牛,这时1天约需要饲料940kg。饲养员李大叔估计平均每只大牛1天约需饲料18至20kg,每只小牛1天约需要饲料7至8kg。请你通过计算检验李大叔的估计是否正确?1、怎样检验他的估计呢?2、题目中包含怎样的等量关系?(1)30只大牛1天所需饲料+15只
小牛1天所需饲料=1天的饲料总量;(2)42只大牛1天所需饲料+20只小
牛1天所需饲料=后来1天的饲料总量.等量关系解:设平均每只大牛和每只小牛1天各约用饲料 x kg和ykg解这个方程组得x=20y=5这就是说,每只大牛1天约需饲料____kg,每只小牛1天约需饲料____kg.因此,饲料员李大叔对大牛的食量估计______,对小牛的食量估计_____.
205较准确偏高列方程组解应用题的步骤:审
列
解
验
答弄清题目中的数量关系,设出两个未知数
分析题意,找出两个等量关系,列出方程组
解出方程组,求出未知数的值检验求得的值是否正确和符合实际情形
写出答案
植物园门票价格如下表所示: 某校初一(1), (2)两个班共104人去植物园春游,其中(1)班人数较少,不到50人,(2)班人数较多,有50多人.经估算如果两班都以班为单位分别购票,则一共应付1240元.
问题:你能否算出两个班各有多少名学生?
想一想:你认为他们如何购票比较合算?
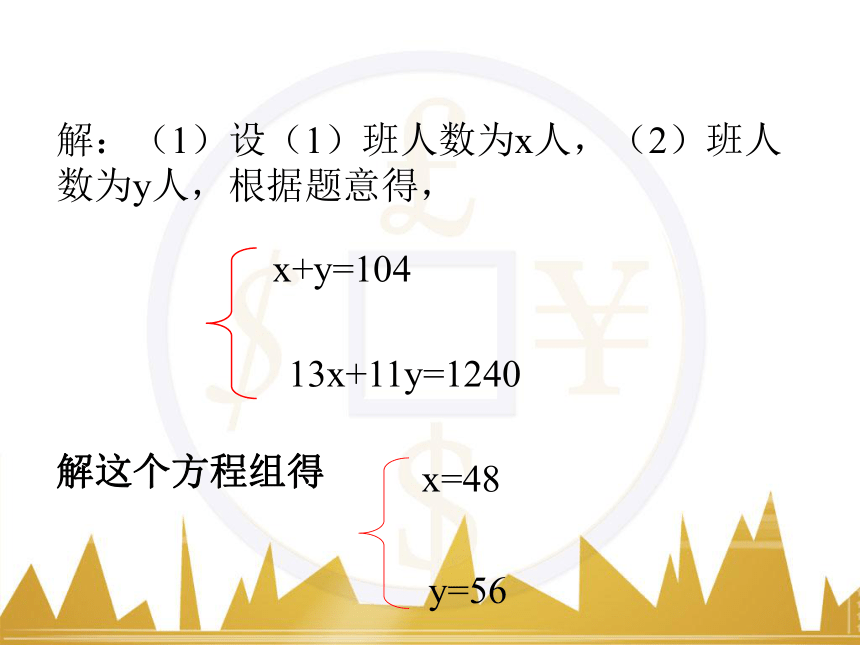
解:(1)设(1)班人数为x人,(2)班人数为y人,根据题意得,
x+y=104
13x+11y=1240解这个方程组得
x=48
y=56
(2)两个班一起买票合理。
因为单独买票共需1240元,而一起买票需要:9(x+y)=9×104=936元;
936﹤1240,所以选择一起买票划算。
某高校共有5个大餐厅和2个小餐厅,经过测试:同时开放1个大餐厅和2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅和1个小餐厅,可供2280名学生就餐. (1)求1个大餐厅和1个小餐厅分别可供多少名学生就餐? (2)若7个餐厅同时开放,请估计一下能否供应全校的5300名学生就餐?请说明理由.解: (1)设1个大餐厅和1个小餐厅分别可供x名,y名学生就餐,x+2y=16802x+y=2280解得:x=960y=360(2)若7个餐厅同时开放,则有
5×960+2×360=5320答: (1) 1个大餐厅和1个小餐厅分别可供960名,360名学生就餐. (2)若7个餐厅同时开放,可以供应全校的5300名学生就餐.5320>5300依题意得
实际问题 数学问题
[方程(组)]数学问题的解
实际问题
的答案 常用的基本等量关系行程问题:
(1)追击问题
(2)相遇问题
(3)航行问题:
①船在静水中的速度+水速=船的顺水速度;
②船在静水中的速度-水速=船的逆水速度;
③顺水速度-逆水速度=2×水速。工程问题:工作效率×工作时间=工作量.甲乙两队合作:甲的工作总量+乙的工作总量=1商品销售利润问题(“成本”可以说成“进价”)
(1)利润=售价-成本;
(2) ;
(3)利润=成本×利润率;
(4)标价=成本×(1+利润率);
(5)实际售价=标价×打折率;储蓄问题:
(1)基本概念:
①本金②利息③本息和
(2)计算公式
①利息=本金×利率×期数
②本息和=本金+利息=本金+本金×利率×期数=本金× (1+利率×期数)
增长率问题:
原量×(1+增长率)=增长后的量;
原量×(1-减少率)=减少后的量。浓度问题
溶液质量×浓度=溶质质量年龄问题:
关键:是抓住两人年龄的增长数是相等,两人的年龄差是永远不会变的优化方案问题
需要从几种方案中,选择最佳方案,如网络的使用、到不同旅行社购票等,一般都要运用方程解答,得出最佳方案。 一片青草地,每天的匀速长出青草,这片青草可供27头牛吃6周或23头牛吃9周。那么这片草地可供21头牛吃几周?
解:设每天长出草量够X头牛吃,现有的草量够Y头牛 吃,得
27×6=6X+Y 解得 x=15
23×9=9X+Y y=72
设够21头牛吃a天则
21×a=15×a+72
解得a=12
答:这片草地够21头牛吃12天。1.行程问题:1.相遇问题:甲的路程+乙的路程=总的路程
(环形跑道):甲的路程+乙的路程=一圈长2.追及问题:快者的路程-慢者的路程=原来相距路
程
(环形跑道): 快者的路程-慢者的路程=一圈长
3.顺逆问题:顺速=静速+水(风)速
逆速=静速-水(风)速例1.某人要在规定的时间内由甲地赶往乙地,如果他以每小时50千米的速度行驶,就会迟到24分钟,如果他以每小时75千米的速度行驶,就会提前24分钟 到达乙地,求甲、乙两地间的距离.
、解:设甲、乙两地间的距离为S千米,规定
时间为t小时,根据题意得方程组例2.甲、乙二人以不变的速度在环形路上跑步,如果同时同地出发,相向而行,每隔2分钟相遇一次;如果同向而行,每隔6分钟相遇一次.已知甲比乙跑得快,甲、乙每分钟各跑多少圈?解:设甲、乙二人每分钟各跑x、y圈,根据
题意得方程组解得答:甲、乙二人每分钟各跑
、 圈,4.销售问题:
标价×折扣=售价
售价-进价=利润
利润率=1.已知甲.乙两种商品的标价和为100元,因市场变化,甲商品打9折,乙商品提价5﹪,调价后,甲.乙两种商品的售价和比标价和提高了2﹪,求甲.乙两种商品的标价各是多少? 答:甲种商品的标价是20元,乙种商品的标价是80元.解:设甲、乙两种商品的标价分别为x、y元,
根据题意,得解这个方程组,得
悟空顺风探妖踪,
千里只行四分钟.
归时四分行六百,
风速多少才称雄?顺风速度=悟空飞行速度+风速
逆风速度=悟空飞行速度-风速
解:设悟空飞行速度是每分钟x里, 风速是每分钟y里,4(x-y)=600 x=200 y=50答:风速是每分钟50里.4(x+y)=1000 解得:依题意得
养牛场原有30只大牛和15只小牛,1天约需要饲料675kg;一周后又购进12只大牛和5只小牛,这时1天约需要饲料940kg。饲养员李大叔估计平均每只大牛1天约需饲料18至20kg,每只小牛1天约需要饲料7至8kg。请你通过计算检验李大叔的估计是否正确?1、怎样检验他的估计呢?2、题目中包含怎样的等量关系?(1)30只大牛1天所需饲料+15只
小牛1天所需饲料=1天的饲料总量;(2)42只大牛1天所需饲料+20只小
牛1天所需饲料=后来1天的饲料总量.等量关系解:设平均每只大牛和每只小牛1天各约用饲料 x kg和ykg解这个方程组得x=20y=5这就是说,每只大牛1天约需饲料____kg,每只小牛1天约需饲料____kg.因此,饲料员李大叔对大牛的食量估计______,对小牛的食量估计_____.
205较准确偏高列方程组解应用题的步骤:审
列
解
验
答弄清题目中的数量关系,设出两个未知数
分析题意,找出两个等量关系,列出方程组
解出方程组,求出未知数的值检验求得的值是否正确和符合实际情形
写出答案
植物园门票价格如下表所示: 某校初一(1), (2)两个班共104人去植物园春游,其中(1)班人数较少,不到50人,(2)班人数较多,有50多人.经估算如果两班都以班为单位分别购票,则一共应付1240元.
问题:你能否算出两个班各有多少名学生?
想一想:你认为他们如何购票比较合算?
解:(1)设(1)班人数为x人,(2)班人数为y人,根据题意得,
x+y=104
13x+11y=1240解这个方程组得
x=48
y=56
(2)两个班一起买票合理。
因为单独买票共需1240元,而一起买票需要:9(x+y)=9×104=936元;
936﹤1240,所以选择一起买票划算。
某高校共有5个大餐厅和2个小餐厅,经过测试:同时开放1个大餐厅和2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅和1个小餐厅,可供2280名学生就餐. (1)求1个大餐厅和1个小餐厅分别可供多少名学生就餐? (2)若7个餐厅同时开放,请估计一下能否供应全校的5300名学生就餐?请说明理由.解: (1)设1个大餐厅和1个小餐厅分别可供x名,y名学生就餐,x+2y=16802x+y=2280解得:x=960y=360(2)若7个餐厅同时开放,则有
5×960+2×360=5320答: (1) 1个大餐厅和1个小餐厅分别可供960名,360名学生就餐. (2)若7个餐厅同时开放,可以供应全校的5300名学生就餐.5320>5300依题意得
实际问题 数学问题
[方程(组)]数学问题的解
实际问题
的答案 常用的基本等量关系行程问题:
(1)追击问题
(2)相遇问题
(3)航行问题:
①船在静水中的速度+水速=船的顺水速度;
②船在静水中的速度-水速=船的逆水速度;
③顺水速度-逆水速度=2×水速。工程问题:工作效率×工作时间=工作量.甲乙两队合作:甲的工作总量+乙的工作总量=1商品销售利润问题(“成本”可以说成“进价”)
(1)利润=售价-成本;
(2) ;
(3)利润=成本×利润率;
(4)标价=成本×(1+利润率);
(5)实际售价=标价×打折率;储蓄问题:
(1)基本概念:
①本金②利息③本息和
(2)计算公式
①利息=本金×利率×期数
②本息和=本金+利息=本金+本金×利率×期数=本金× (1+利率×期数)
增长率问题:
原量×(1+增长率)=增长后的量;
原量×(1-减少率)=减少后的量。浓度问题
溶液质量×浓度=溶质质量年龄问题:
关键:是抓住两人年龄的增长数是相等,两人的年龄差是永远不会变的优化方案问题
需要从几种方案中,选择最佳方案,如网络的使用、到不同旅行社购票等,一般都要运用方程解答,得出最佳方案。 一片青草地,每天的匀速长出青草,这片青草可供27头牛吃6周或23头牛吃9周。那么这片草地可供21头牛吃几周?
解:设每天长出草量够X头牛吃,现有的草量够Y头牛 吃,得
27×6=6X+Y 解得 x=15
23×9=9X+Y y=72
设够21头牛吃a天则
21×a=15×a+72
解得a=12
答:这片草地够21头牛吃12天。1.行程问题:1.相遇问题:甲的路程+乙的路程=总的路程
(环形跑道):甲的路程+乙的路程=一圈长2.追及问题:快者的路程-慢者的路程=原来相距路
程
(环形跑道): 快者的路程-慢者的路程=一圈长
3.顺逆问题:顺速=静速+水(风)速
逆速=静速-水(风)速例1.某人要在规定的时间内由甲地赶往乙地,如果他以每小时50千米的速度行驶,就会迟到24分钟,如果他以每小时75千米的速度行驶,就会提前24分钟 到达乙地,求甲、乙两地间的距离.
、解:设甲、乙两地间的距离为S千米,规定
时间为t小时,根据题意得方程组例2.甲、乙二人以不变的速度在环形路上跑步,如果同时同地出发,相向而行,每隔2分钟相遇一次;如果同向而行,每隔6分钟相遇一次.已知甲比乙跑得快,甲、乙每分钟各跑多少圈?解:设甲、乙二人每分钟各跑x、y圈,根据
题意得方程组解得答:甲、乙二人每分钟各跑
、 圈,4.销售问题:
标价×折扣=售价
售价-进价=利润
利润率=1.已知甲.乙两种商品的标价和为100元,因市场变化,甲商品打9折,乙商品提价5﹪,调价后,甲.乙两种商品的售价和比标价和提高了2﹪,求甲.乙两种商品的标价各是多少? 答:甲种商品的标价是20元,乙种商品的标价是80元.解:设甲、乙两种商品的标价分别为x、y元,
根据题意,得解这个方程组,得
