新人教版高中数学选择性必修第三册7.2 离散型随机变量及其分布列(共20张PPT)
文档属性
| 名称 | 新人教版高中数学选择性必修第三册7.2 离散型随机变量及其分布列(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-25 10:28:13 | ||
图片预览







文档简介
(共20张PPT)
7.2 离散型随机变量及其分布列
1.了解随机变量及离散型随机变量的含义,会用离散型随机变量描述随机现象.
2.理解取有限个值的离散型随机变量及其分布列的概念与性质.
3.会求某些简单的离散型随机变量的分布列.
4.理解两点分布的定义,并能简单运用.
第七章 随机变量及其分布
1 |随机变量与离散型随机变量
1.随机变量
(1)定义:一般地,对于随机试验样本空间Ω中的每个样本点ω,都有① 唯一的 实
数X(ω)与之对应,我们称X为随机变量.
(2)表示:通常用大写英文字母表示随机变量,用小写英文字母表示随机变量的取值.
(3)随机变量与函数的关系
联系:随机变量与函数都是一种对应关系,样本点ω相当于函数定义中的自变量,样
本空间Ω相当于函数的定义域.
区别:样本空间Ω不一定是数集,随机变量的取值X(ω)随着试验结果ω的变化而变化,
而函数是数集到数集的对应.
2.离散型随机变量
可能取值为② 有限个 或可以③ 一一列举 的随机变量,称为离散型随机变量.
第七章 随机变量及其分布
2 |离散型随机变量X的分布列
1.定义
一般地,设离散型随机变量X的可能取值为x1,x2,…,xn,我们称X取每一个值xi的概率P
(X=xi)=pi,i=1,2,…,n为X的概率分布列,简称分布列.
2.分布列的表格表示
X x1 x2 … xn
P p1 p2 … pn
分布列也可以用等式形式表示为P(X=xi)=pi,i=1,2,…,n,还可以用图形表示.
第七章 随机变量及其分布
3.离散型随机变量分布列具有的两个性质:
(1)pi④ ≥ 0,i=1,2,…,n;
(2)p1+p2+…+pn= ⑤ 1 .
4.求离散型随机变量X的分布列的步骤(其中i=1,2,…,n):
第七章 随机变量及其分布
3 |两点分布(0-1分布)
如果P(A)=p,则P( )=⑥ 1-p ,那么X的分布列如表所示.
X 0 1
P 1-p p
我们称X服从两点分布或0-1分布.
第七章 随机变量及其分布
1.随机变量的取值可以是有限个,也可以是无限个. ( √ )
2.在离散型随机变量分布列中,每个随机变量的取值所对应的概率都可以为任意的
实数. ( )
在离散型随机变量分布列中,每个随机变量的取值对应的概率均在[0,1]范围内.
3.在离散型随机变量分布列中,所有概率之和为1. ( √ )
4.离散型随机变量的可能取值表示的事件是彼此互斥的. ( √ )
5.离散型随机变量分布列中,每个随机变量的取值对应概率都相等. ( )
分布列中的每个随机变量代表的随机事件,并非都是等可能发生的事件.
6.若随机变量X的分布列如表所示,则X服从两点分布. ( )
判断正误,正确的画“ √” ,错误的画“ ” .
服从两点分布的随机变量的可能取值为0,1.
第七章 随机变量及其分布
1 |以统计图表为背景的分布列问题
以统计图表为背景的考题,最终落脚点一般都是对随机变量概率分布的研究,
解题时先通过统计图表获取相关数据,再求出随机变量的分布列.
第七章 随机变量及其分布
空气质 量指数 (0,50] (50,100] (100,150] (150,200] (200,250] (250,300]
空气质 量等级 1级优 2级良 3级轻度 污染 4级中度 污染 5级重度 污染 6级重度
污染
某中学的环保社团制作了该校所在区域空气质量指数与空气质量等级对应关系的
表格(假设该区域空气质量指数不会超过300):
第七章 随机变量及其分布
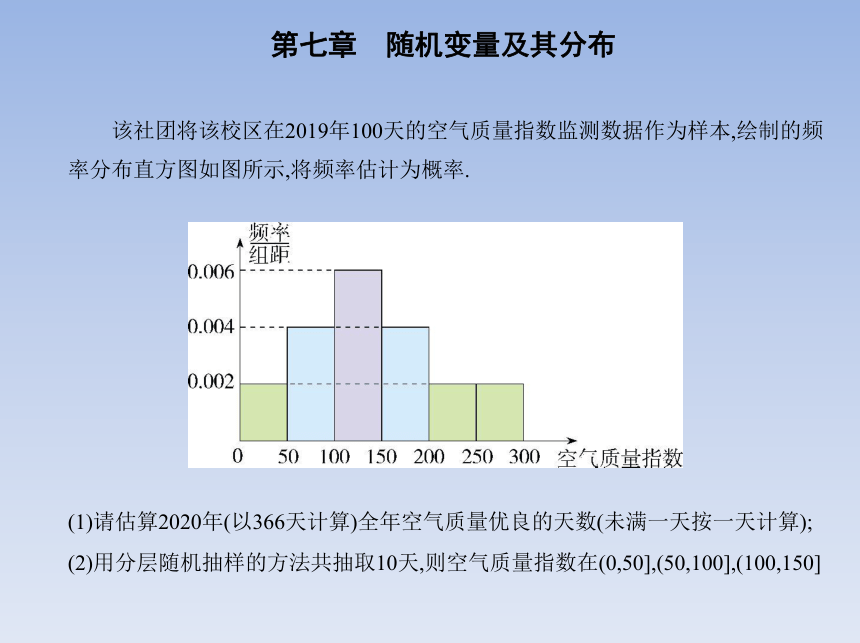
该社团将该校区在2019年100天的空气质量指数监测数据作为样本,绘制的频
率分布直方图如图所示,将频率估计为概率.
(1)请估算2020年(以366天计算)全年空气质量优良的天数(未满一天按一天计算);
(2)用分层随机抽样的方法共抽取10天,则空气质量指数在(0,50],(50,100],(100,150]
第七章 随机变量及其分布
的天数中各应抽取多少个样本
(3)已知空气质量等级为1级时不需要净化空气,空气质量等级为2级时每天需净化
空气的费用为2 000元,空气质量等级为3级时每天需净化空气的费用为4 000元,若
在(2)的条件下,从空气质量指数在(0,150]的天数中任意抽取两天,求这两天的净化
空气总费用X的分布列.
思路点拨
(1)根据频率分布直方图,由频率估计概率,即可求出全年空气质量优良的天数.
(2)由频率分布直方图,分别求得空气质量指数在(0,50],(50,100]和(100,150]的概率
即可求解.
(3)根据题意,得到随机变量X的可能取值为2 000,4 000,6 000,8 000,分别求得相应的
概率,进而列出随机变量X的分布列.
第七章 随机变量及其分布
解析 (1)根据频率分布直方图可估算2020年(以366天计算)全年空气质量优良的
天数为
(0.002+0.004)×50×366=109.8≈110.
(2)由频率分布直方图可得,空气质量指数在(0,50]的概率为0.002×50=0.1,所以10天
中抽的天数为10×0.1=1,空气质量指数在(50,100]的概率为0.004×50=0.2,所以10天
中抽的天数为10×0.2=2,空气质量指数在(100,150]的概率为0.006×50=0.3,所以10天
中抽的天数为10×0.3=3.
所以空气质量指数在(0,50],(50,100],(100,150]的天数中各应抽取1,2,3个样本.
(3)由题意知X的可能取值为2 000,4 000,6 000,8 000.
P(X=2 000)= = ,P(X=4 000)= = ,
P(X=6 000)= = ,P(X=8 000)= = .
第七章 随机变量及其分布
可得X的分布列如表所示.
X 2 000 4 000 6 000 8 000
P
第七章 随机变量及其分布
2 |两个相关的随机变量的分布列问题
1.一般地,若X是随机变量,则Y=f(X)也是随机变量.
2.已知随机变量X的分布列,求随机变量Y=f(X)的分布列,其关键是弄清X取每一个
值时相对应的Y的值,若f(X)的取值出现重复,则需要把它们的相应概率相加,所求即
为Y的取值概率.
第七章 随机变量及其分布
(2020四川绵阳高二下期末)某超市举办酬宾活动,单次购物超过100元的顾客可参
与一次抽奖活动,活动规则如下:盒子中装有大小和形状完全相同的7个小球,其中3
个红球、2个白球和2个黑球,从中不放回地随机抽取2个球,每个球被抽到的机会均
等.每抽到1个红球记0分,每抽到1个白球记50分,每抽到1个黑球记100分.若抽取2个
球的总得分为200分,则可获得10元现金,若总得分低于100分,则没有现金,其余得分可获得5元现金.
(1)设抽取2个球的总得分为随机变量X,求X的分布列;
(2)设每位顾客一次抽奖获得现金Y元,求Y的分布列.
第七章 随机变量及其分布
思路点拨
(1)由题意得X的可能取值为0,50,100,150,200,分别求出相应的概率,由此得出X的分
布列.
(2)由题意得Y的可能取值为0,5,10,分别求出相应的概率,由此得出Y的分布列.
解析 (1)随机变量X的可能取值为0,50,100,150,200.
P(X=0)= = ,
P(X=50)= = ,
P(X=100)= = ,
P(X=150)= = ,
P(X=200)= = .
可得X的分布列如表所示.
第七章 随机变量及其分布
X 0 50 100 150 200
P
(2)由(1)知Y=f(X)=
所以P(Y=0)=P(X=0)+P(X=50)= + = ,
P(Y=5)=P(X=100)+P(X=150)= + = ,
P(Y=10)=P(X=200)= .
可得Y的分布列如表所示.
Y 0 5 10
P
第七章 随机变量及其分布
3 |离散型随机变量的分布列及其综合应用
1.离散型随机变量的分布列是计数原理、排列组合、概率求解与其他知识的
综合.解决此类问题的关键:
(1)理清随机变量的可能取值;
(2)理清随机变量取某些值时对应的事件是什么;
(3)利用两个计数原理及排列、组合的知识求出试验的样本空间与所求事件所包
含的样本点数.
2.离散型随机变量的性质容易和其他知识相结合,所涉及的参数范围(最值)问题容
易与函数、基本不等式相结合,做题时需注意分布列的性质与其他模块内容的联
系.
第七章 随机变量及其分布
私家车的尾气排放是造成雾霾天气的重要因素之一,因此在生活中我们应该提倡
低碳生活,少开私家车,尽量选择绿色的出行方式,为减少雾霾天气出一份力.为此,
很多城市实施了机动车尾号限行措施,我市某报社为了解市区公众对“车辆限
行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
年龄 (岁) [15, 25) [25, 35) [35, 45) [45, 55) [55, 65) [65,
75]
频数 5 10 15 10 5 5
赞成 人数 4 6 9 6 3 4
第七章 随机变量及其分布
(1)若从年龄在[15,25),[25,35)的被调查者中各随机选取2人进行追踪调查,求恰
有2人不赞成的概率;
(2)在(1)的条件下,记选取的4人中不赞成“车辆限行”的人数为X,求X的分布列.
思路点拨
(1)先根据2人所在年龄段分类,再分别求对应概率,最后根据概率的加法公式求解.
(2)先确定X的可能取值,再分别求对应概率,列表可得分布列.
解析 (1)由题表知年龄在[15,25)内的有5人,不赞成的有1人,年龄在[25,35)内的有1
0人,不赞成的有4人,从这两组的所有被调查者中各随机选取2人,恰有2人不赞成的
概率
P= × + × = .
(2)X的可能取值为0,1,2,3.
第七章 随机变量及其分布
P(X=0)= × = ,
P(X=1)= × + × = ,
P(X=2)= × + × = ,
P(X=3)= × = .
可得X的分布列如表所示.
X 0 1 2 3
P
第七章 随机变量及其分布
7.2 离散型随机变量及其分布列
1.了解随机变量及离散型随机变量的含义,会用离散型随机变量描述随机现象.
2.理解取有限个值的离散型随机变量及其分布列的概念与性质.
3.会求某些简单的离散型随机变量的分布列.
4.理解两点分布的定义,并能简单运用.
第七章 随机变量及其分布
1 |随机变量与离散型随机变量
1.随机变量
(1)定义:一般地,对于随机试验样本空间Ω中的每个样本点ω,都有① 唯一的 实
数X(ω)与之对应,我们称X为随机变量.
(2)表示:通常用大写英文字母表示随机变量,用小写英文字母表示随机变量的取值.
(3)随机变量与函数的关系
联系:随机变量与函数都是一种对应关系,样本点ω相当于函数定义中的自变量,样
本空间Ω相当于函数的定义域.
区别:样本空间Ω不一定是数集,随机变量的取值X(ω)随着试验结果ω的变化而变化,
而函数是数集到数集的对应.
2.离散型随机变量
可能取值为② 有限个 或可以③ 一一列举 的随机变量,称为离散型随机变量.
第七章 随机变量及其分布
2 |离散型随机变量X的分布列
1.定义
一般地,设离散型随机变量X的可能取值为x1,x2,…,xn,我们称X取每一个值xi的概率P
(X=xi)=pi,i=1,2,…,n为X的概率分布列,简称分布列.
2.分布列的表格表示
X x1 x2 … xn
P p1 p2 … pn
分布列也可以用等式形式表示为P(X=xi)=pi,i=1,2,…,n,还可以用图形表示.
第七章 随机变量及其分布
3.离散型随机变量分布列具有的两个性质:
(1)pi④ ≥ 0,i=1,2,…,n;
(2)p1+p2+…+pn= ⑤ 1 .
4.求离散型随机变量X的分布列的步骤(其中i=1,2,…,n):
第七章 随机变量及其分布
3 |两点分布(0-1分布)
如果P(A)=p,则P( )=⑥ 1-p ,那么X的分布列如表所示.
X 0 1
P 1-p p
我们称X服从两点分布或0-1分布.
第七章 随机变量及其分布
1.随机变量的取值可以是有限个,也可以是无限个. ( √ )
2.在离散型随机变量分布列中,每个随机变量的取值所对应的概率都可以为任意的
实数. ( )
在离散型随机变量分布列中,每个随机变量的取值对应的概率均在[0,1]范围内.
3.在离散型随机变量分布列中,所有概率之和为1. ( √ )
4.离散型随机变量的可能取值表示的事件是彼此互斥的. ( √ )
5.离散型随机变量分布列中,每个随机变量的取值对应概率都相等. ( )
分布列中的每个随机变量代表的随机事件,并非都是等可能发生的事件.
6.若随机变量X的分布列如表所示,则X服从两点分布. ( )
判断正误,正确的画“ √” ,错误的画“ ” .
服从两点分布的随机变量的可能取值为0,1.
第七章 随机变量及其分布
1 |以统计图表为背景的分布列问题
以统计图表为背景的考题,最终落脚点一般都是对随机变量概率分布的研究,
解题时先通过统计图表获取相关数据,再求出随机变量的分布列.
第七章 随机变量及其分布
空气质 量指数 (0,50] (50,100] (100,150] (150,200] (200,250] (250,300]
空气质 量等级 1级优 2级良 3级轻度 污染 4级中度 污染 5级重度 污染 6级重度
污染
某中学的环保社团制作了该校所在区域空气质量指数与空气质量等级对应关系的
表格(假设该区域空气质量指数不会超过300):
第七章 随机变量及其分布
该社团将该校区在2019年100天的空气质量指数监测数据作为样本,绘制的频
率分布直方图如图所示,将频率估计为概率.
(1)请估算2020年(以366天计算)全年空气质量优良的天数(未满一天按一天计算);
(2)用分层随机抽样的方法共抽取10天,则空气质量指数在(0,50],(50,100],(100,150]
第七章 随机变量及其分布
的天数中各应抽取多少个样本
(3)已知空气质量等级为1级时不需要净化空气,空气质量等级为2级时每天需净化
空气的费用为2 000元,空气质量等级为3级时每天需净化空气的费用为4 000元,若
在(2)的条件下,从空气质量指数在(0,150]的天数中任意抽取两天,求这两天的净化
空气总费用X的分布列.
思路点拨
(1)根据频率分布直方图,由频率估计概率,即可求出全年空气质量优良的天数.
(2)由频率分布直方图,分别求得空气质量指数在(0,50],(50,100]和(100,150]的概率
即可求解.
(3)根据题意,得到随机变量X的可能取值为2 000,4 000,6 000,8 000,分别求得相应的
概率,进而列出随机变量X的分布列.
第七章 随机变量及其分布
解析 (1)根据频率分布直方图可估算2020年(以366天计算)全年空气质量优良的
天数为
(0.002+0.004)×50×366=109.8≈110.
(2)由频率分布直方图可得,空气质量指数在(0,50]的概率为0.002×50=0.1,所以10天
中抽的天数为10×0.1=1,空气质量指数在(50,100]的概率为0.004×50=0.2,所以10天
中抽的天数为10×0.2=2,空气质量指数在(100,150]的概率为0.006×50=0.3,所以10天
中抽的天数为10×0.3=3.
所以空气质量指数在(0,50],(50,100],(100,150]的天数中各应抽取1,2,3个样本.
(3)由题意知X的可能取值为2 000,4 000,6 000,8 000.
P(X=2 000)= = ,P(X=4 000)= = ,
P(X=6 000)= = ,P(X=8 000)= = .
第七章 随机变量及其分布
可得X的分布列如表所示.
X 2 000 4 000 6 000 8 000
P
第七章 随机变量及其分布
2 |两个相关的随机变量的分布列问题
1.一般地,若X是随机变量,则Y=f(X)也是随机变量.
2.已知随机变量X的分布列,求随机变量Y=f(X)的分布列,其关键是弄清X取每一个
值时相对应的Y的值,若f(X)的取值出现重复,则需要把它们的相应概率相加,所求即
为Y的取值概率.
第七章 随机变量及其分布
(2020四川绵阳高二下期末)某超市举办酬宾活动,单次购物超过100元的顾客可参
与一次抽奖活动,活动规则如下:盒子中装有大小和形状完全相同的7个小球,其中3
个红球、2个白球和2个黑球,从中不放回地随机抽取2个球,每个球被抽到的机会均
等.每抽到1个红球记0分,每抽到1个白球记50分,每抽到1个黑球记100分.若抽取2个
球的总得分为200分,则可获得10元现金,若总得分低于100分,则没有现金,其余得分可获得5元现金.
(1)设抽取2个球的总得分为随机变量X,求X的分布列;
(2)设每位顾客一次抽奖获得现金Y元,求Y的分布列.
第七章 随机变量及其分布
思路点拨
(1)由题意得X的可能取值为0,50,100,150,200,分别求出相应的概率,由此得出X的分
布列.
(2)由题意得Y的可能取值为0,5,10,分别求出相应的概率,由此得出Y的分布列.
解析 (1)随机变量X的可能取值为0,50,100,150,200.
P(X=0)= = ,
P(X=50)= = ,
P(X=100)= = ,
P(X=150)= = ,
P(X=200)= = .
可得X的分布列如表所示.
第七章 随机变量及其分布
X 0 50 100 150 200
P
(2)由(1)知Y=f(X)=
所以P(Y=0)=P(X=0)+P(X=50)= + = ,
P(Y=5)=P(X=100)+P(X=150)= + = ,
P(Y=10)=P(X=200)= .
可得Y的分布列如表所示.
Y 0 5 10
P
第七章 随机变量及其分布
3 |离散型随机变量的分布列及其综合应用
1.离散型随机变量的分布列是计数原理、排列组合、概率求解与其他知识的
综合.解决此类问题的关键:
(1)理清随机变量的可能取值;
(2)理清随机变量取某些值时对应的事件是什么;
(3)利用两个计数原理及排列、组合的知识求出试验的样本空间与所求事件所包
含的样本点数.
2.离散型随机变量的性质容易和其他知识相结合,所涉及的参数范围(最值)问题容
易与函数、基本不等式相结合,做题时需注意分布列的性质与其他模块内容的联
系.
第七章 随机变量及其分布
私家车的尾气排放是造成雾霾天气的重要因素之一,因此在生活中我们应该提倡
低碳生活,少开私家车,尽量选择绿色的出行方式,为减少雾霾天气出一份力.为此,
很多城市实施了机动车尾号限行措施,我市某报社为了解市区公众对“车辆限
行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
年龄 (岁) [15, 25) [25, 35) [35, 45) [45, 55) [55, 65) [65,
75]
频数 5 10 15 10 5 5
赞成 人数 4 6 9 6 3 4
第七章 随机变量及其分布
(1)若从年龄在[15,25),[25,35)的被调查者中各随机选取2人进行追踪调查,求恰
有2人不赞成的概率;
(2)在(1)的条件下,记选取的4人中不赞成“车辆限行”的人数为X,求X的分布列.
思路点拨
(1)先根据2人所在年龄段分类,再分别求对应概率,最后根据概率的加法公式求解.
(2)先确定X的可能取值,再分别求对应概率,列表可得分布列.
解析 (1)由题表知年龄在[15,25)内的有5人,不赞成的有1人,年龄在[25,35)内的有1
0人,不赞成的有4人,从这两组的所有被调查者中各随机选取2人,恰有2人不赞成的
概率
P= × + × = .
(2)X的可能取值为0,1,2,3.
第七章 随机变量及其分布
P(X=0)= × = ,
P(X=1)= × + × = ,
P(X=2)= × + × = ,
P(X=3)= × = .
可得X的分布列如表所示.
X 0 1 2 3
P
第七章 随机变量及其分布
