新人教版高中数学选择性必修第三册7.4.1 二项分布(共16张PPT)
文档属性
| 名称 | 新人教版高中数学选择性必修第三册7.4.1 二项分布(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-25 10:33:45 | ||
图片预览





文档简介
(共16张PPT)
7.4 二项分布与超几何分布
7.4.1 二项分布
1.了解n重伯努利试验及其特征.
2.理解二项分布及其期望、方差.
3.能利用n重伯努利试验的模型及二项分布解决简单的实际问题.
第七章 随机变量及其分布
1 |伯努利试验
1.伯努利试验的概念
把只包含① 两个 可能结果的试验叫做伯努利试验.
2. n重伯努利试验的两个特征
(1)同一个伯努利试验重复做n次;
(2)各次试验的结果② 相互独立 .
第七章 随机变量及其分布
1.伯努利试验只包含两个可能结果. ( √ )
2.n重伯努利试验中,各次试验结果之间没有影响. ( √ )
3.在n重伯努利试验中,各次试验中事件发生的概率可以不同. ( )
4.n重伯努利试验中事件A恰好发生k次与事件A恰好在第k次发生不一样. ( √ )
5.某同学投篮的命中率为0.6,他10次投篮命中的次数X是一个随机变量,且X~B(10,
0.6). ( √ )
6.若X~B(5,0.4),则E(X)=2,D(X)=3. ( )
判断正误,正确的画“ √” ,错误的画“ ” .
第七章 随机变量及其分布
2 |二项分布
一般地,在n重伯努利试验中,设每次试验中事件A发生的概率为p(0表示事件A发生的次数,则X的分布列为P(X=k)=③ pk(1-p)n-k ,k=0,1,2,…,n.如果
随机变量X的分布列具有上式的形式,则称随机变量X服从二项分布,记作X~
④ B(n,p) .
3 |二项分布的期望与方差
一般地,如果X~B(n,p),那么E(X)=⑤ np ,D(X)=⑥ np(1-p) .
第七章 随机变量及其分布
1 |二项分布的实际应用
利用二项分布模型解决实际问题的一般步骤
(1)根据题意设出随机变量;
(2)分析随机变量是否服从二项分布;
(3)若服从二项分布,则求出参数n和p的值;
(4)根据需要列出相关式子并解决问题.
解决二项分布问题的两个关注点
(1)公式P(X=k)= pk(1-p)n-k(k=0,1,2,…,n)必须在满足“独立重复试验”时才能运用,
否则不能应用该公式.
(2)判断一个随机变量是否服从二项分布,关键有两点:一是对立性,即一次试验中,
事件发生与否,二者必居其一;二是重复性,即试验是否独立重复地进行了n次.
第七章 随机变量及其分布
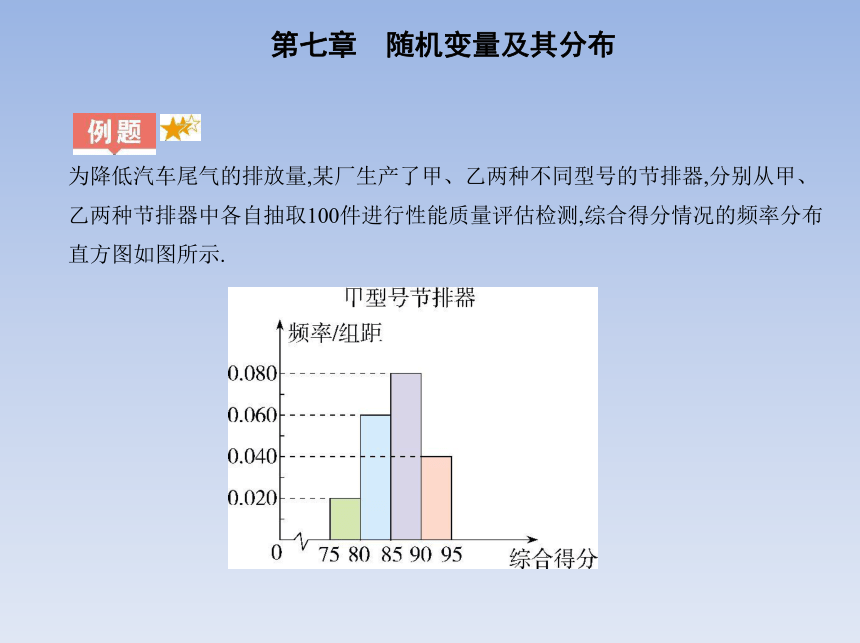
为降低汽车尾气的排放量,某厂生产了甲、乙两种不同型号的节排器,分别从甲、
乙两种节排器中各自抽取100件进行性能质量评估检测,综合得分情况的频率分布
直方图如图所示.
第七章 随机变量及其分布
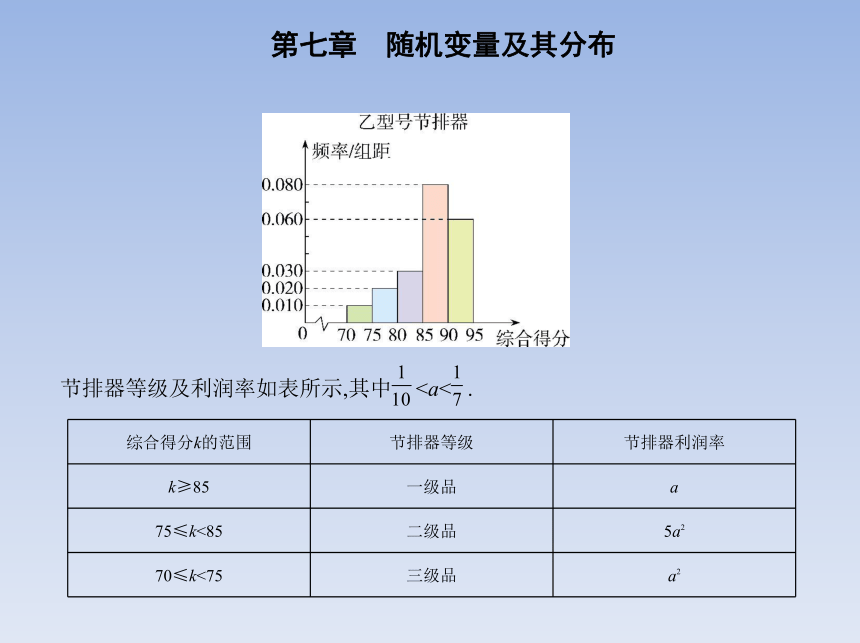
节排器等级及利润率如表所示,其中综合得分k的范围 节排器等级 节排器利润率
k≥85 一级品 a
75≤k<85 二级品 5a2
70≤k<75 三级品 a2
第七章 随机变量及其分布
(1)若从这100件甲型号节排器中,按节排器等级用分层随机抽样的方法抽取10
件,再从这10件节排器中随机抽取3件,求至少有2件一级品的概率;
(2)视频率分布直方图中的频率为概率,用样本估计总体,则
①若从乙型号节排器中随机抽取3件,求其中二级品的件数X的分布列及数学期望E
(X);
②从长期来看,投资哪种型号的节排器平均利润率较大
思路点拨
(1)由已知及频率分布直方图中的信息知,甲型号节排器中的一级品的概率为 ,根
据分层随机抽样,计算抽取的10件节排器中一级品的件数,再求出从中随机抽取3
件,至少有2件一级品的概率.
(2)①由已知及频率分布直方图中的信息知,乙型号节排器中的一级品的概率为 ,
第七章 随机变量及其分布
二级品的概率为 ,三级品的概率为 ,若从乙型号节排器中随机抽取3件,则二级
品的件数X的可能取值为0,1,2,3,且X~B ,由此能求出X的分布列和数学期望;
②分别求出甲型号节排器利润率的平均值和乙型号节排器利润率的平均值,由此
得出投资乙型号节排器的平均利润率较大.
解析 (1)由已知及频率分布直方图中的信息知,甲型号节排器中的一级品的概率
为 ,
用分层随机抽样的方法抽取10件,则抽取一级品的件数为10× =6.
故从这10件中随机抽取3件,至少有2件一级品的概率P= = .
(2)①由已知及频率分布直方图中的信息知,乙型号节排器中的一级品的概率为 ,
第七章 随机变量及其分布
二级品的概率为 ,三级品的概率为 ,若从乙型号节排器中随机抽取3件,则其中
二级品的件数X的可能取值为0,1,2,3,且X~B ,
所以P(X=0)= = ,
P(X=1)= = ,
P(X=2)= = ,
P(X=3)= = .
可得X的分布列如表所示.
X 0 1 2 3
P
第七章 随机变量及其分布
所以E(X)=0× +1× +2× +3× = .
②由题意知,甲型号节排器的平均利润率
E1= a+ ×5a2=2a2+ a,
乙型号节排器的平均利润率
E2= a+ ×5a2+ a2= a2+ a,
E1-E2= a2- a= a ,
又所以投资乙型号节排器的平均利润率较大.
第七章 随机变量及其分布
2 |二项分布中的最大值
求二项分布中的最大值的步骤
(1)由X~B(n,p),得P(X=k)= pk(1-p)n-k,k=0,1,2,…,n.
(2)令P(X=k)-P(X=k-1)≥0或 ≥1,求出k的取值区间,此区间即为P(X=k)的
单调递增区间,它的补集区间为单调递减区间.
(3)结合P(X=k)的单调性确定P(X=k)的最大值和对应的k的值.
第七章 随机变量及其分布
为了引导居民合理用水,某市决定全面实施阶梯水价.阶梯水价原则上以住宅(一套
住宅为一户)的月用水量为基准定价,具体划分标准如表所示.
阶梯级别 第一阶梯 第二阶梯 第三阶梯
月用水量范围 (单位:立方米) (0,10] (10,15] (15,+∞)
从本市随机抽取了10户家庭(编号为1~10),统计了他们某月的用水量,得到如
下表格:
家庭编号 1 2 3 4 5 6 7 8 9 10
月用水量(单位:立
方米) 7 10 11 12 13 13 14 15 20 32
第七章 随机变量及其分布
(1)现要在这10户家庭中任意选取3户,求取到月用水量为第二阶梯的户数X的
分布列;
(2)用抽到的10户家庭的月用水量作为样本估计全市居民的用水情况,现从全市随
机抽取10户,若抽到k户月用水量为第二阶梯的可能性最大,求k的值.
解析 (1)由题中表格可知,抽取的10户家庭中月用水量为第一阶梯的有2户,第二
阶梯的有6户,第三阶梯的有2户,
故取到月用水量为第二阶梯的户数X的可能取值为0,1,2,3.
P(X=0)= = ,
P(X=1)= = ,
P(X=2)= = ,
第七章 随机变量及其分布
P(X=3)= = .
可得X的分布列如表所示.
X 0 1 2 3
P
(2)设Y为从全市抽取的10户中月用水量为第二阶梯的家庭户数,依题意得Y~B
,
所以P(Y=k)= ,
其中k=0,1,2,…,10.
第七章 随机变量及其分布
设t= = = ,
若t>1,则k<6.6,此时P(Y=k-1)若t<1,则k>6.6,此时P(Y=k-1)>P(Y=k),
所以当k=6或k=7时,P(Y=k)的值最大.
因为 = = >1,
所以k的值为6.
第七章 随机变量及其分布
7.4 二项分布与超几何分布
7.4.1 二项分布
1.了解n重伯努利试验及其特征.
2.理解二项分布及其期望、方差.
3.能利用n重伯努利试验的模型及二项分布解决简单的实际问题.
第七章 随机变量及其分布
1 |伯努利试验
1.伯努利试验的概念
把只包含① 两个 可能结果的试验叫做伯努利试验.
2. n重伯努利试验的两个特征
(1)同一个伯努利试验重复做n次;
(2)各次试验的结果② 相互独立 .
第七章 随机变量及其分布
1.伯努利试验只包含两个可能结果. ( √ )
2.n重伯努利试验中,各次试验结果之间没有影响. ( √ )
3.在n重伯努利试验中,各次试验中事件发生的概率可以不同. ( )
4.n重伯努利试验中事件A恰好发生k次与事件A恰好在第k次发生不一样. ( √ )
5.某同学投篮的命中率为0.6,他10次投篮命中的次数X是一个随机变量,且X~B(10,
0.6). ( √ )
6.若X~B(5,0.4),则E(X)=2,D(X)=3. ( )
判断正误,正确的画“ √” ,错误的画“ ” .
第七章 随机变量及其分布
2 |二项分布
一般地,在n重伯努利试验中,设每次试验中事件A发生的概率为p(0
随机变量X的分布列具有上式的形式,则称随机变量X服从二项分布,记作X~
④ B(n,p) .
3 |二项分布的期望与方差
一般地,如果X~B(n,p),那么E(X)=⑤ np ,D(X)=⑥ np(1-p) .
第七章 随机变量及其分布
1 |二项分布的实际应用
利用二项分布模型解决实际问题的一般步骤
(1)根据题意设出随机变量;
(2)分析随机变量是否服从二项分布;
(3)若服从二项分布,则求出参数n和p的值;
(4)根据需要列出相关式子并解决问题.
解决二项分布问题的两个关注点
(1)公式P(X=k)= pk(1-p)n-k(k=0,1,2,…,n)必须在满足“独立重复试验”时才能运用,
否则不能应用该公式.
(2)判断一个随机变量是否服从二项分布,关键有两点:一是对立性,即一次试验中,
事件发生与否,二者必居其一;二是重复性,即试验是否独立重复地进行了n次.
第七章 随机变量及其分布
为降低汽车尾气的排放量,某厂生产了甲、乙两种不同型号的节排器,分别从甲、
乙两种节排器中各自抽取100件进行性能质量评估检测,综合得分情况的频率分布
直方图如图所示.
第七章 随机变量及其分布
节排器等级及利润率如表所示,其中
k≥85 一级品 a
75≤k<85 二级品 5a2
70≤k<75 三级品 a2
第七章 随机变量及其分布
(1)若从这100件甲型号节排器中,按节排器等级用分层随机抽样的方法抽取10
件,再从这10件节排器中随机抽取3件,求至少有2件一级品的概率;
(2)视频率分布直方图中的频率为概率,用样本估计总体,则
①若从乙型号节排器中随机抽取3件,求其中二级品的件数X的分布列及数学期望E
(X);
②从长期来看,投资哪种型号的节排器平均利润率较大
思路点拨
(1)由已知及频率分布直方图中的信息知,甲型号节排器中的一级品的概率为 ,根
据分层随机抽样,计算抽取的10件节排器中一级品的件数,再求出从中随机抽取3
件,至少有2件一级品的概率.
(2)①由已知及频率分布直方图中的信息知,乙型号节排器中的一级品的概率为 ,
第七章 随机变量及其分布
二级品的概率为 ,三级品的概率为 ,若从乙型号节排器中随机抽取3件,则二级
品的件数X的可能取值为0,1,2,3,且X~B ,由此能求出X的分布列和数学期望;
②分别求出甲型号节排器利润率的平均值和乙型号节排器利润率的平均值,由此
得出投资乙型号节排器的平均利润率较大.
解析 (1)由已知及频率分布直方图中的信息知,甲型号节排器中的一级品的概率
为 ,
用分层随机抽样的方法抽取10件,则抽取一级品的件数为10× =6.
故从这10件中随机抽取3件,至少有2件一级品的概率P= = .
(2)①由已知及频率分布直方图中的信息知,乙型号节排器中的一级品的概率为 ,
第七章 随机变量及其分布
二级品的概率为 ,三级品的概率为 ,若从乙型号节排器中随机抽取3件,则其中
二级品的件数X的可能取值为0,1,2,3,且X~B ,
所以P(X=0)= = ,
P(X=1)= = ,
P(X=2)= = ,
P(X=3)= = .
可得X的分布列如表所示.
X 0 1 2 3
P
第七章 随机变量及其分布
所以E(X)=0× +1× +2× +3× = .
②由题意知,甲型号节排器的平均利润率
E1= a+ ×5a2=2a2+ a,
乙型号节排器的平均利润率
E2= a+ ×5a2+ a2= a2+ a,
E1-E2= a2- a= a ,
又
第七章 随机变量及其分布
2 |二项分布中的最大值
求二项分布中的最大值的步骤
(1)由X~B(n,p),得P(X=k)= pk(1-p)n-k,k=0,1,2,…,n.
(2)令P(X=k)-P(X=k-1)≥0或 ≥1,求出k的取值区间,此区间即为P(X=k)的
单调递增区间,它的补集区间为单调递减区间.
(3)结合P(X=k)的单调性确定P(X=k)的最大值和对应的k的值.
第七章 随机变量及其分布
为了引导居民合理用水,某市决定全面实施阶梯水价.阶梯水价原则上以住宅(一套
住宅为一户)的月用水量为基准定价,具体划分标准如表所示.
阶梯级别 第一阶梯 第二阶梯 第三阶梯
月用水量范围 (单位:立方米) (0,10] (10,15] (15,+∞)
从本市随机抽取了10户家庭(编号为1~10),统计了他们某月的用水量,得到如
下表格:
家庭编号 1 2 3 4 5 6 7 8 9 10
月用水量(单位:立
方米) 7 10 11 12 13 13 14 15 20 32
第七章 随机变量及其分布
(1)现要在这10户家庭中任意选取3户,求取到月用水量为第二阶梯的户数X的
分布列;
(2)用抽到的10户家庭的月用水量作为样本估计全市居民的用水情况,现从全市随
机抽取10户,若抽到k户月用水量为第二阶梯的可能性最大,求k的值.
解析 (1)由题中表格可知,抽取的10户家庭中月用水量为第一阶梯的有2户,第二
阶梯的有6户,第三阶梯的有2户,
故取到月用水量为第二阶梯的户数X的可能取值为0,1,2,3.
P(X=0)= = ,
P(X=1)= = ,
P(X=2)= = ,
第七章 随机变量及其分布
P(X=3)= = .
可得X的分布列如表所示.
X 0 1 2 3
P
(2)设Y为从全市抽取的10户中月用水量为第二阶梯的家庭户数,依题意得Y~B
,
所以P(Y=k)= ,
其中k=0,1,2,…,10.
第七章 随机变量及其分布
设t= = = ,
若t>1,则k<6.6,此时P(Y=k-1)
所以当k=6或k=7时,P(Y=k)的值最大.
因为 = = >1,
所以k的值为6.
第七章 随机变量及其分布
