新人教版高中数学选择性必修第三册7.5 正态分布(共17张PPT)
文档属性
| 名称 | 新人教版高中数学选择性必修第三册7.5 正态分布(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-25 10:35:07 | ||
图片预览






文档简介
(共17张PPT)
7.5 正态分布
1.通过误差模型,了解服从正态分布的随机变量.
2.通过具体实例,借助频率分布直方图的几何直观,了解正态分布的特征.
3.了解正态分布的均值、方差及其含义.
第七章 随机变量及其分布
1 |连续型随机变量
随机变量的取值充满某个区间甚至整个实轴,但取一点的概率为0,称这类随机变量
为连续型随机变量.
第七章 随机变量及其分布
2 |正态分布
1.正态曲线
函数f(x)= ,x∈R.其中μ∈R,σ>0为参数.我们称f(x)为① 正态密度函数 ,
称它的图象为② 正态密度曲线 ,简称正态曲线.
2. 正态分布
若随机变量X的概率密度函数为f(x),则称随机变量X服从正态分布,记为X~③ N(μ,
σ2) .特别地,当μ=0,σ=1时,称随机变量X服从④ 标准正态分布 .
第七章 随机变量及其分布
3 |正态曲线的特点
正态曲线有以下特点:
(1)曲线位于x轴⑤ 上方 ,与x轴⑥ 不相交 ;
(2)曲线是单峰的,它关于直线⑦ x=μ 对称;
(3)曲线在⑧ x=μ 处达到峰值 ;
(4)当|x|无限⑨ 增大 时,曲线无限接近x轴;
(5)对任意的σ>0,曲线与x轴围成的面积总为1;
(6)在参数σ取固定值时,正态曲线的位置由μ确定,且随着μ的变化而沿x轴平移,如图
甲所示;
第七章 随机变量及其分布
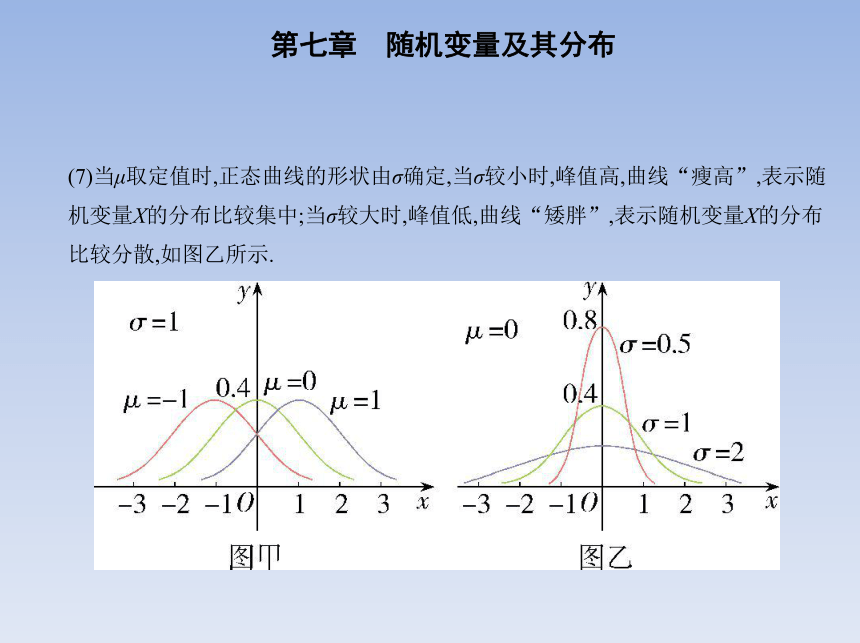
(7)当μ取定值时,正态曲线的形状由σ确定,当σ较小时,峰值高,曲线“瘦高”,表示随
机变量X的分布比较集中;当σ较大时,峰值低,曲线“矮胖”,表示随机变量X的分布
比较分散,如图乙所示.
第七章 随机变量及其分布
4 |正态总体在三个特殊区间内取值的概率
P(μ-σ≤X≤μ+σ)≈⑩ 0.682 7 ;
P(μ-2σ≤X≤μ+2σ)≈ 0.954 5 ;
P(μ-3σ≤X≤μ+3σ)≈ 0.997 3 .
5 | 3σ原则
在实际应用中,通常认为服从于正态分布N(μ,σ2)的随机变量X只取 [μ-3σ,μ
+3σ] 中的值,这在统计学中称为3σ原则.
第七章 随机变量及其分布
1.正态密度函数中的参数μ,σ的意义分别是样本的均值和方差. ( )
2.正态曲线是单峰的,其与x轴围成的面积是随参数μ,σ的变化而变化的. ( )
3.正态曲线可以关于y轴对称. ( √ )
4.在正态分布中,参数μ是反映随机变量取值的平均水平的特征数,可以用样本均值
去估计;σ是衡量随机变量总体波动大小的特征数,可以用样本标准差去估计. ( √ )
5.若随机变量X~N(μ,σ2),则X可以是离散型随机变量.( )
6.正态曲线的对称轴的位置由μ确定,曲线形状由σ确定.( √ )
判断正误,正确的画“ √” ,错误的画“ ” .
第七章 随机变量及其分布
1 |正态分布的概率问题
在正态分布下求概率的关键在于充分恰当地利用正态曲线的对称性,把待求
概率的区间转化为已知概率的区间.当条件中无已知概率时,则要将区间转化为三
个特殊区间:[μ-σ,μ+σ][μ-2σ,μ+2σ],[μ-3σ,μ+3σ].利用随机变量X在这三个特殊区间
取值的概率进行计算.
一般地,若随机变量X服从正态分布N(μ,σ2),则由直线x=μ是正态密度曲线的对称轴
可知:
(1)P(X≥a)=1-P(X(2)对任意的实数a,有P(X≤μ-a)=P(X≥μ+a);
(3)P(a≤X≤b)=P(X≤b)-P(X第七章 随机变量及其分布
2 |正态分布的实际应用
2019年4月,河北、辽宁、江苏、福建、湖北、湖南、广东、重庆8省市发布高考
综合改革实施方案,方案决定从2018年秋季入学的高中一年级学生开始实施高考
综合改革.考生总成绩由全国统一高考的语文、数学、外语3个科目成绩和考生选
择的3科普通高中学业水平选择性考试科目成绩组成,满分为750分,即通常所说的
“3+1+2”模式.所谓“3+1+2”,即“3”是三门主科,分别是语文、数学、外语,这
三门科目是必选的,“1”指的是要在物理、历史里选一门,按原始分计入成绩,
“2”指考生要在生物、化学、思想政治、地理4门中选择2门,但是这几门科目不
以原始分计入成绩,而是等级赋分.等级赋分指的是把考生的原始成绩根据人数的
比例分为A、B、C、D、E五个等级,五个等级分别对应着相应的分数区间,然后再
用公式换算,转换得出分数.
第七章 随机变量及其分布
1.某教育部门为了调查学生语文、数学、外语三科成绩与选科之间的关系,从当地
不同层次的学校中抽取高一学生2 500名参加语文、数学、外语的网络测试,满分4
50分,测试结果如下:此次测试平均成绩为171分,351分以上的有57人,该次网络测试
成绩基本服从正态分布.现给前400名颁发荣誉证书,若考生甲得知他的成绩为270
分,问甲能否进入前400名
附:若随机变量X服从正态分布(μ,σ2),则P(μ-σ≤X≤μ+σ)≈0.682 7,P(μ-2σ≤X≤μ+2
σ)≈0.954 5,P(μ-3σ≤X≤μ+3σ)≈0.997 3.
提示:设此次网络测试的成绩为X,由题意可知X~N(171,σ2).
因为 =0.022 8,且 ≈ =0.022 75≈0.022 8,
所以σ= =90,
第七章 随机变量及其分布
所以X~N(171,902).
而 =0.16,
且P(X>μ+σ)= ≈ =0.158 65<0.16,
所以前400名学生成绩的最低分低于μ+σ=261,
而考生甲的成绩为270分,所以甲同学能进入前400名.
第七章 随机变量及其分布
2.考生丙得知他的实际成绩为430分,而考生乙告诉考生丙:“这次测试平均成绩为
201分,351分以上的有57人.”请结合统计学知识帮助丙同学辨别乙同学信息的真
伪.
提示:假设考生乙所说为真,则μ=201,
P(X>μ+2σ)= ≈ =0.022 75≈0.022 8,
而 =0.022 8,所以σ= =75,
从而μ+3σ=201+3×75=426,
而430 [μ-3σ,μ+3σ],
因为X>μ+3σ为小概率事件,所以丙同学的成绩为430分是小概率事件,可认为其不
可能发生,但却又发生了,所以可认为乙同学所说为假.
第七章 随机变量及其分布
利用服从正态分布N(μ,σ2)的随机变量X在三个特殊区间上取值的概率,可以解决两
类实际问题:
一类是估计在某一范围内的数量,具体方法是先确定随机变量在该范围内取值的
概率,再乘样本容量即可.
另一类是利用3σ原则作决策.决策步骤如下:①确定一次试验中取值a是否落入范围
[μ-3σ,μ+3σ];②作出判断,若a∈[μ-3σ,μ+3σ],则接受统计假设,若a [μ-3σ,μ+3σ],则
拒绝统计假设.
第七章 随机变量及其分布
从某企业生产的某种产品中随机抽取100件,测量这些产品的一项质量指标值,由测
量结果得频率分布直方图如图.
第七章 随机变量及其分布
(1)求这100件产品质量指标值的平均数 和方差s2(同一组的数据用该组区间的中
点值作为代表);
(2)由频率分布直方图可以认为,这种产品的质量指标值Z服从正态分布N(μ,σ2),其
中μ近似为样本平均数 ,σ2近似为样本方差s2.
(i)若某用户从该企业购买了10件这种产品,记X表示这10件产品中质量指标值位于
[187.4,225.2]的产品件数,求E(X);
(ii)一天内抽取的产品中,若出现了质量指标值在[μ-3σ,μ+3σ]之外的产品,就认为这
一天的生产过程中可能出现了异常情况,需对当天的生产过程进行检查.下面的表
格记录了检验员在一天内抽取的15个产品(编号为1~15)的质量指标值,根据近似值
判断是否需要对当天的生产过程进行检查.
第七章 随机变量及其分布
产品编号 1 2 3 4 5
质量指标值 162.3 173.5 188 189.6 194
产品编号 6 7 8 9 10
质量指标值 194.9 199 204 206.3 207.2
产品编号 11 12 13 14 15
质量指标值 216 216.7 227 228.1 237.9
附: ≈12.6.若X~N(μ,σ2),则P(μ-σ≤X≤μ+σ)≈0.682 7,P(μ-2σ≤X≤μ+2σ)≈
0.954 5,P(μ-3σ≤X≤μ+3σ)≈0.997 3.
第七章 随机变量及其分布
思路点拨
(1)根据频率分布直方图可得平均数和方差.
(2)(i)根据Z服从正态分布可求得X~B(10,0.818 6),由二项分布的均值公式即可求解;
(ii)μ-3σ≈162.2,μ+3σ≈237.8,237.9 [162.2,237.8],利用3σ原则得到结果.
解析 (1)由题意得, =170×0.025+180×0.09+190×0.22+200×0.32+210×0.24+220×0.
08+230×0.025=200,
s2=(-30)2×0.025+(-20)2×0.09+(-10)2×0.22+02×0.32+102×0.24+202×0.08+302×0.025=159.
(2)(i)由题意得,一件产品的质量指标值位于区间[187.4,225.2]的概率约为
=0.818 6,则X~B(10,0.818 6),
∴E(X)=10×0.818 6=8.186.
(ii)由(1)知,μ-3σ≈200-12.6×3=162.2,μ+3σ≈200+12.6×3=237.8.
∵237.9 [162.2,237.8],∴需要对当天的生产过程进行检查.
第七章 随机变量及其分布
7.5 正态分布
1.通过误差模型,了解服从正态分布的随机变量.
2.通过具体实例,借助频率分布直方图的几何直观,了解正态分布的特征.
3.了解正态分布的均值、方差及其含义.
第七章 随机变量及其分布
1 |连续型随机变量
随机变量的取值充满某个区间甚至整个实轴,但取一点的概率为0,称这类随机变量
为连续型随机变量.
第七章 随机变量及其分布
2 |正态分布
1.正态曲线
函数f(x)= ,x∈R.其中μ∈R,σ>0为参数.我们称f(x)为① 正态密度函数 ,
称它的图象为② 正态密度曲线 ,简称正态曲线.
2. 正态分布
若随机变量X的概率密度函数为f(x),则称随机变量X服从正态分布,记为X~③ N(μ,
σ2) .特别地,当μ=0,σ=1时,称随机变量X服从④ 标准正态分布 .
第七章 随机变量及其分布
3 |正态曲线的特点
正态曲线有以下特点:
(1)曲线位于x轴⑤ 上方 ,与x轴⑥ 不相交 ;
(2)曲线是单峰的,它关于直线⑦ x=μ 对称;
(3)曲线在⑧ x=μ 处达到峰值 ;
(4)当|x|无限⑨ 增大 时,曲线无限接近x轴;
(5)对任意的σ>0,曲线与x轴围成的面积总为1;
(6)在参数σ取固定值时,正态曲线的位置由μ确定,且随着μ的变化而沿x轴平移,如图
甲所示;
第七章 随机变量及其分布
(7)当μ取定值时,正态曲线的形状由σ确定,当σ较小时,峰值高,曲线“瘦高”,表示随
机变量X的分布比较集中;当σ较大时,峰值低,曲线“矮胖”,表示随机变量X的分布
比较分散,如图乙所示.
第七章 随机变量及其分布
4 |正态总体在三个特殊区间内取值的概率
P(μ-σ≤X≤μ+σ)≈⑩ 0.682 7 ;
P(μ-2σ≤X≤μ+2σ)≈ 0.954 5 ;
P(μ-3σ≤X≤μ+3σ)≈ 0.997 3 .
5 | 3σ原则
在实际应用中,通常认为服从于正态分布N(μ,σ2)的随机变量X只取 [μ-3σ,μ
+3σ] 中的值,这在统计学中称为3σ原则.
第七章 随机变量及其分布
1.正态密度函数中的参数μ,σ的意义分别是样本的均值和方差. ( )
2.正态曲线是单峰的,其与x轴围成的面积是随参数μ,σ的变化而变化的. ( )
3.正态曲线可以关于y轴对称. ( √ )
4.在正态分布中,参数μ是反映随机变量取值的平均水平的特征数,可以用样本均值
去估计;σ是衡量随机变量总体波动大小的特征数,可以用样本标准差去估计. ( √ )
5.若随机变量X~N(μ,σ2),则X可以是离散型随机变量.( )
6.正态曲线的对称轴的位置由μ确定,曲线形状由σ确定.( √ )
判断正误,正确的画“ √” ,错误的画“ ” .
第七章 随机变量及其分布
1 |正态分布的概率问题
在正态分布下求概率的关键在于充分恰当地利用正态曲线的对称性,把待求
概率的区间转化为已知概率的区间.当条件中无已知概率时,则要将区间转化为三
个特殊区间:[μ-σ,μ+σ][μ-2σ,μ+2σ],[μ-3σ,μ+3σ].利用随机变量X在这三个特殊区间
取值的概率进行计算.
一般地,若随机变量X服从正态分布N(μ,σ2),则由直线x=μ是正态密度曲线的对称轴
可知:
(1)P(X≥a)=1-P(X
(3)P(a≤X≤b)=P(X≤b)-P(X
2 |正态分布的实际应用
2019年4月,河北、辽宁、江苏、福建、湖北、湖南、广东、重庆8省市发布高考
综合改革实施方案,方案决定从2018年秋季入学的高中一年级学生开始实施高考
综合改革.考生总成绩由全国统一高考的语文、数学、外语3个科目成绩和考生选
择的3科普通高中学业水平选择性考试科目成绩组成,满分为750分,即通常所说的
“3+1+2”模式.所谓“3+1+2”,即“3”是三门主科,分别是语文、数学、外语,这
三门科目是必选的,“1”指的是要在物理、历史里选一门,按原始分计入成绩,
“2”指考生要在生物、化学、思想政治、地理4门中选择2门,但是这几门科目不
以原始分计入成绩,而是等级赋分.等级赋分指的是把考生的原始成绩根据人数的
比例分为A、B、C、D、E五个等级,五个等级分别对应着相应的分数区间,然后再
用公式换算,转换得出分数.
第七章 随机变量及其分布
1.某教育部门为了调查学生语文、数学、外语三科成绩与选科之间的关系,从当地
不同层次的学校中抽取高一学生2 500名参加语文、数学、外语的网络测试,满分4
50分,测试结果如下:此次测试平均成绩为171分,351分以上的有57人,该次网络测试
成绩基本服从正态分布.现给前400名颁发荣誉证书,若考生甲得知他的成绩为270
分,问甲能否进入前400名
附:若随机变量X服从正态分布(μ,σ2),则P(μ-σ≤X≤μ+σ)≈0.682 7,P(μ-2σ≤X≤μ+2
σ)≈0.954 5,P(μ-3σ≤X≤μ+3σ)≈0.997 3.
提示:设此次网络测试的成绩为X,由题意可知X~N(171,σ2).
因为 =0.022 8,且 ≈ =0.022 75≈0.022 8,
所以σ= =90,
第七章 随机变量及其分布
所以X~N(171,902).
而 =0.16,
且P(X>μ+σ)= ≈ =0.158 65<0.16,
所以前400名学生成绩的最低分低于μ+σ=261,
而考生甲的成绩为270分,所以甲同学能进入前400名.
第七章 随机变量及其分布
2.考生丙得知他的实际成绩为430分,而考生乙告诉考生丙:“这次测试平均成绩为
201分,351分以上的有57人.”请结合统计学知识帮助丙同学辨别乙同学信息的真
伪.
提示:假设考生乙所说为真,则μ=201,
P(X>μ+2σ)= ≈ =0.022 75≈0.022 8,
而 =0.022 8,所以σ= =75,
从而μ+3σ=201+3×75=426,
而430 [μ-3σ,μ+3σ],
因为X>μ+3σ为小概率事件,所以丙同学的成绩为430分是小概率事件,可认为其不
可能发生,但却又发生了,所以可认为乙同学所说为假.
第七章 随机变量及其分布
利用服从正态分布N(μ,σ2)的随机变量X在三个特殊区间上取值的概率,可以解决两
类实际问题:
一类是估计在某一范围内的数量,具体方法是先确定随机变量在该范围内取值的
概率,再乘样本容量即可.
另一类是利用3σ原则作决策.决策步骤如下:①确定一次试验中取值a是否落入范围
[μ-3σ,μ+3σ];②作出判断,若a∈[μ-3σ,μ+3σ],则接受统计假设,若a [μ-3σ,μ+3σ],则
拒绝统计假设.
第七章 随机变量及其分布
从某企业生产的某种产品中随机抽取100件,测量这些产品的一项质量指标值,由测
量结果得频率分布直方图如图.
第七章 随机变量及其分布
(1)求这100件产品质量指标值的平均数 和方差s2(同一组的数据用该组区间的中
点值作为代表);
(2)由频率分布直方图可以认为,这种产品的质量指标值Z服从正态分布N(μ,σ2),其
中μ近似为样本平均数 ,σ2近似为样本方差s2.
(i)若某用户从该企业购买了10件这种产品,记X表示这10件产品中质量指标值位于
[187.4,225.2]的产品件数,求E(X);
(ii)一天内抽取的产品中,若出现了质量指标值在[μ-3σ,μ+3σ]之外的产品,就认为这
一天的生产过程中可能出现了异常情况,需对当天的生产过程进行检查.下面的表
格记录了检验员在一天内抽取的15个产品(编号为1~15)的质量指标值,根据近似值
判断是否需要对当天的生产过程进行检查.
第七章 随机变量及其分布
产品编号 1 2 3 4 5
质量指标值 162.3 173.5 188 189.6 194
产品编号 6 7 8 9 10
质量指标值 194.9 199 204 206.3 207.2
产品编号 11 12 13 14 15
质量指标值 216 216.7 227 228.1 237.9
附: ≈12.6.若X~N(μ,σ2),则P(μ-σ≤X≤μ+σ)≈0.682 7,P(μ-2σ≤X≤μ+2σ)≈
0.954 5,P(μ-3σ≤X≤μ+3σ)≈0.997 3.
第七章 随机变量及其分布
思路点拨
(1)根据频率分布直方图可得平均数和方差.
(2)(i)根据Z服从正态分布可求得X~B(10,0.818 6),由二项分布的均值公式即可求解;
(ii)μ-3σ≈162.2,μ+3σ≈237.8,237.9 [162.2,237.8],利用3σ原则得到结果.
解析 (1)由题意得, =170×0.025+180×0.09+190×0.22+200×0.32+210×0.24+220×0.
08+230×0.025=200,
s2=(-30)2×0.025+(-20)2×0.09+(-10)2×0.22+02×0.32+102×0.24+202×0.08+302×0.025=159.
(2)(i)由题意得,一件产品的质量指标值位于区间[187.4,225.2]的概率约为
=0.818 6,则X~B(10,0.818 6),
∴E(X)=10×0.818 6=8.186.
(ii)由(1)知,μ-3σ≈200-12.6×3=162.2,μ+3σ≈200+12.6×3=237.8.
∵237.9 [162.2,237.8],∴需要对当天的生产过程进行检查.
第七章 随机变量及其分布
